What are radians? Simply explained
TLDRThe video script explains the concept of radians in a simple and engaging manner. It uses the analogy of wrapping diameters around a circle to illustrate how pi relates to radians. The presenter clarifies that radians measure angles by the number of radius lengths they span on a circle's circumference. By breaking down half a circle into pi radians and further into fractions like pi/4, pi/3, and 2pi/3, the video helps viewers understand the connection between radians and degrees, emphasizing that radians are essentially about capturing radius lengths on a circle's edge.
Takeaways
- 📏 Pi (π) is the ratio of a circle's circumference to its diameter, representing the number of diameters that can wrap around a circle.
- 🤔 Radians are a way of measuring angles based on the number of radii that can fit around a circle or part of a circle.
- 👀 Understanding radians can be simplified by visualizing how many radii fit around half of a circle, which is π radians.
- 🔄 Pi radians (π radians) is equivalent to 180 degrees, as it represents the angle that corresponds to a half-circle.
- 📐 Radians can be used to express fractions of a circle, such as 1/4 (π/4 radians), 2/3 (2π/3 radians), and so on.
- 🔢 The concept of radians allows for a direct relationship between angles and the circumference of a circle, making calculations in trigonometry more intuitive.
- 🌀 Visualizing radians as capturing radiuses around a circle can help in understanding and calculating angles in radians.
- 📊 The unit circle is a tool that helps in understanding the relationship between radians and degrees, as well as simplifying fractions of a circle.
- 🎓 Tutoring students in radians often involves breaking down the concept into simpler terms, such as relating it to the number of radiuses around a circle.
- 🧠 It's important to be patient and take the time to understand the concept of radians, as it can initially seem complex but becomes easier with a better grasp of the underlying idea.
- 👌 Radians are not just a theoretical concept; they have practical applications in various fields, including physics, engineering, and mathematics.
Q & A
What is the main topic of the video?
-The main topic of the video is radians and how they are used in the context of circles and angles.
Why do some students find radians confusing?
-Students may find radians confusing because they are not as familiar with this unit of angular measure compared to degrees, and the concept of relating angles to the circumference of a circle is abstract.
What is the relationship between pi and the circumference of a circle?
-Pi is the ratio of a circle's circumference to its diameter, indicating that approximately pi diameters can fit around the circle.
How many radians are there in a half circle?
-There are pi radians in a half circle.
What is the definition of a radian?
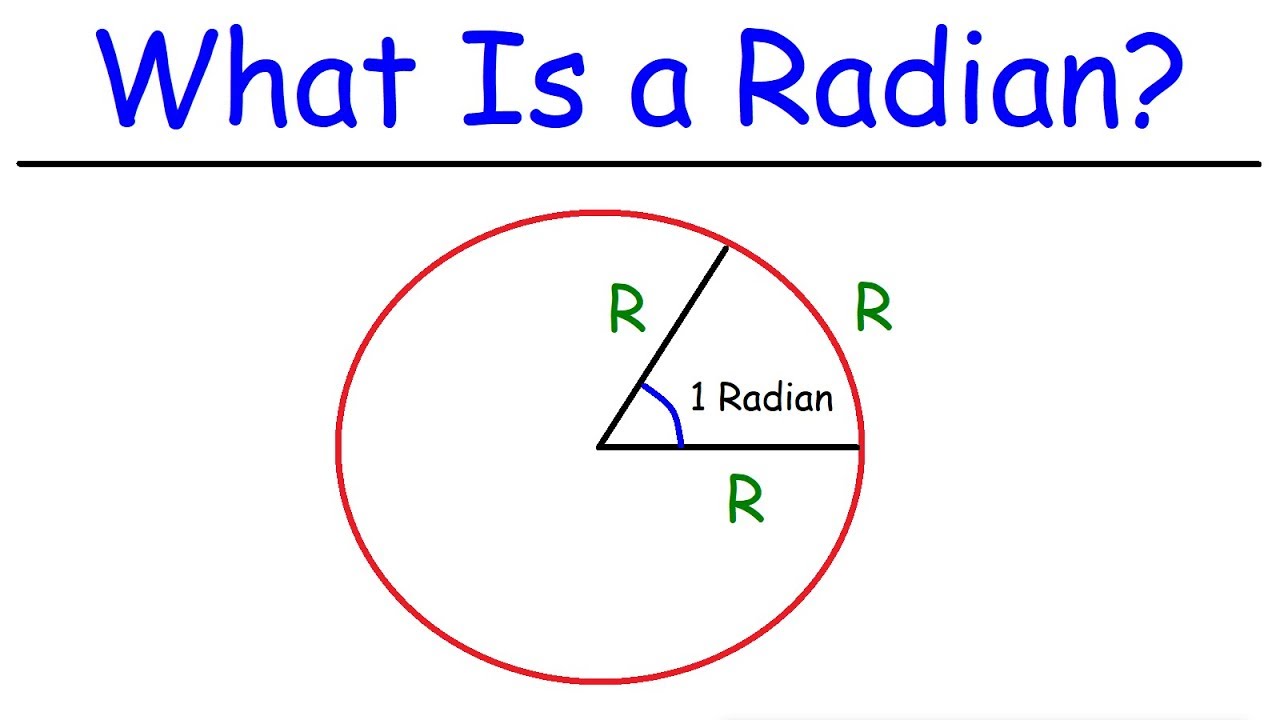
-A radian is the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle.
How can you visualize a radian?
-You can visualize a radian by opening up the central angle of a circle until it 'catches' one radius on the outside of the circle.
What is the significance of understanding fractions of pi in radians?
-Understanding fractions of pi in radians helps in breaking down angles into more manageable parts, such as quarters and sixths of a circle, which simplifies calculations and comparisons.
How many radiuses make up 2pi radians?
-2pi radians capture approximately six radiuses, as it is equivalent to a full circle.
How can you convert between radians and degrees?
-You can convert between radians and degrees by knowing that pi radians is equal to 180 degrees, which can then be used to find equivalent degrees for other fractions of pi.
What is the purpose of using radians in mathematics and physics?
-Radians are used in mathematics and physics because they provide a natural way to measure angles that is directly related to the properties of circles and周期性 functions, making calculations involving these shapes and functions more intuitive and efficient.
How can the concept of radians help with understanding trigonometric functions?
-The concept of radians helps with understanding trigonometric functions by providing a consistent measure of angles that aligns with the periodic nature of these functions, especially when dealing with the unit circle.
Outlines
📚 Introduction to Radians
This paragraph introduces the concept of radians, explaining why they are used and how they relate to the well-known mathematical constant pi. The speaker reassures the audience that radians are easier to understand than they might initially seem, and encourages patience in grasping the concept. The explanation begins with the familiar idea of pi, describing it as the number of diameters that can wrap around a circle. The speaker then transitions to discussing radians by illustrating how a full circle contains pi radii and how a half circle contains pi/2 radians. The goal is to help the audience visualize that a radian is the angle subtended when an arc of a circle intercepts one radius.
🤔 Understanding Radians and Fractions
In this paragraph, the speaker delves deeper into the concept of radians, focusing on their relationship with fractions of pi and degrees. The explanation begins by connecting the idea of pi radians to the concept of a half-circle and how it equates to 180 degrees. The speaker then explores how fractions of pi, such as 1/4 pi and 2/3 pi, can be visualized and understood as quarters and sixths of a circle, respectively. This part of the discussion aims to demystify the concept of radians by showing how they can be broken down into simpler fractions that correspond to familiar segments of a circle. The speaker emphasizes that understanding radians in terms of the number of radiuses intercepted by an angle can make the concept much more intuitive and less intimidating.
Mindmap
Keywords
💡Radians
💡Circle
💡Pi (π)
💡Diameter
💡Trigonometry
💡Tutoring
💡Circumference
💡Central Angle
💡Arc
💡Education
💡Mathematics
Highlights
Radian is a fundamental concept in trigonometry and calculus, which is introduced in the transcript.
The speaker aims to demystify radians for students who find them intimidating, by providing a straightforward explanation.
Pi (π) is related to the circumference of a circle and is the number of diameters that can wrap around it.
The concept of radians is easier to grasp when one understands the relationship between pi and the circle's circumference.
The speaker uses a visual approach to explain radians by imagining opening up the circle and capturing radiuses.
One radian is the angle that 'catches' one radius on the outside of a circle when the circle is 'opened up'.
The number of radians in a circle directly correlates with the number of radiuses that can fit around the circle.
Pi radians is equivalent to 180 degrees, which is the total number of radiuses that can fit around half of a circle.
Fractional radians, such as 1/4 pi or 2/3 pi, can be understood as fractions of 180 degrees.
The speaker emphasizes the importance of patience and taking the time to understand the concept of radians.
Radian is a unit of angular measure that is particularly useful in mathematical calculations involving circles.
The concept of capturing radiuses with radians helps in visualizing the relationship between angles and the circumference of a circle.
The speaker explains how to convert between radians and degrees by relating them to fractions of pi and 180 degrees.
Understanding radians can simplify complex mathematical problems, especially in the study of circles and their properties.
The transcript provides a unique perspective on radians, using the analogy of 'capturing radiuses' to make the concept more accessible.
The speaker's method of explaining radians can be particularly helpful for students who are visual learners.
The transcript offers a practical application of radians in understanding the angles and measurements in a circle.
Transcripts
Browse More Related Video
Trigonometry - What Exactly Is a Radian?

Introduction to Trigonometry: Angles and Radians
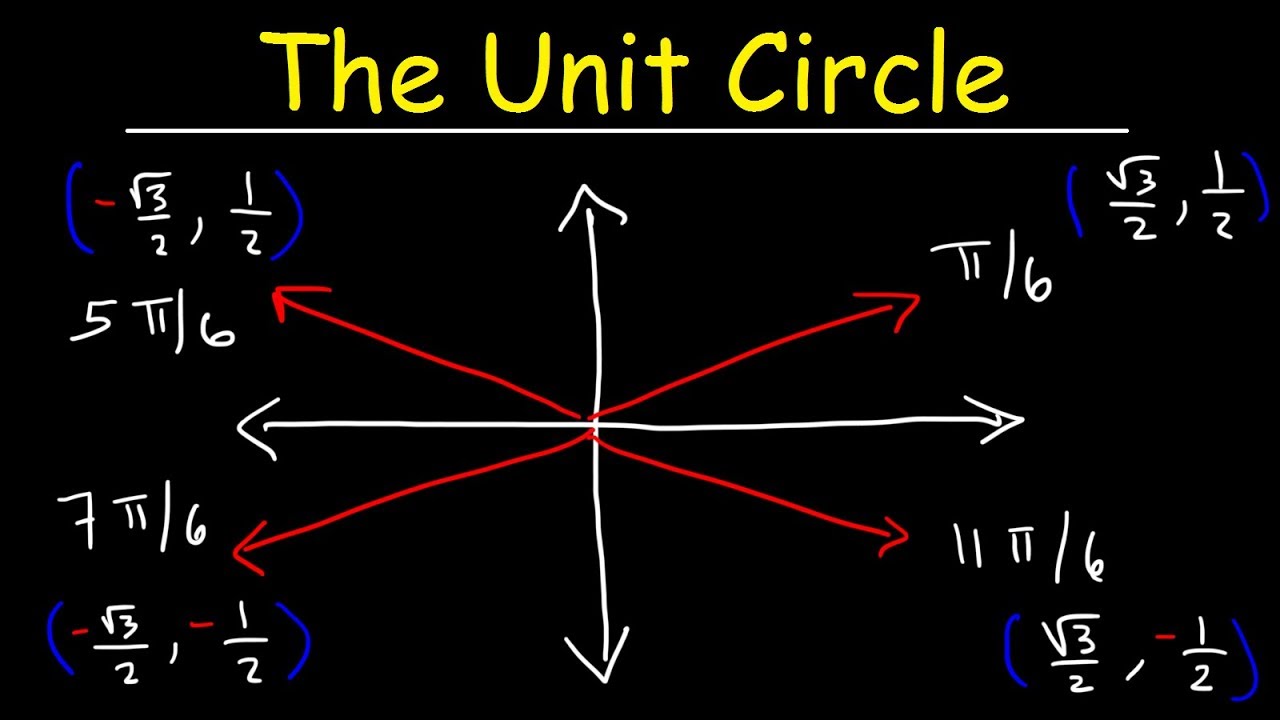
The Unit Circle, Basic Introduction, Trigonometry

Converting Radians and Degrees (Precalculus - Trigonometry 4)
How to Remember the Unit Circle (NancyPi)

CONVERTING DEGREE MEASURE TO RADIAN MEASURE AND VICE VERSA || PRE-CALCULUS
5.0 / 5 (0 votes)
Thanks for rating: