How to Remember the Unit Circle (NancyPi)

NancyPi
2 Oct 201812:02
EducationalLearning
32 Likes 10 Comments

TLDRThe video script is an informative guide on mastering the unit circle in trigonometry. It explains the concept of the unit circle, which is a circle with a radius of one, and its importance in memorizing key trigonometric values. The script outlines the process of identifying angles on the unit circle, starting from the right and moving counter-clockwise, and provides a clear breakdown of the coordinates for angles at Pi/2, Pi, 3Pi/2, and 2Pi radians. It also introduces the concept of dividing these angles further into Pi/4, Pi/6, and Pi/3 to find the corresponding (x, y) coordinates, which are essential for understanding the cosine and sine values. The video emphasizes the patterns and the use of sqrt(2)/2, 1/2, and sqrt(3)/2 in determining these values across different quadrants. The script concludes by relating radian angles to their degree equivalents and encourages viewers to recognize the patterns for easier memorization.

Takeaways
  • πŸ“ The unit circle is a circle with a radius of 1, used as a reference in trigonometry.
  • 🎯 Start angles on the unit circle from the right side and rotate counter-clockwise to reach different angles.
  • πŸŒ€ Angles on the unit circle are measured in radians, with Pi/2, Pi, 3Pi/2, and 2Pi representing quarter-circles.
  • πŸ”’ The pattern for angles within a quarter circle is 1, 3, 5, 7 for Pi/4 angles and 1/2, sqrt(2)/2, sqrt(3)/2 for Pi/6 angles.
  • 🌐 The (x, y) coordinates of a point on the unit circle correspond to the cosine and sine values of the angle.
  • πŸ‘† At the angle of 0, the point (1, 0) corresponds to cos(0) = 1 and sin(0) = 0.
  • πŸ“ˆ For Pi/2, the point (0, 1) corresponds to cos(Pi/2) = 0 and sin(Pi/2) = 1.
  • πŸ“Š At the left side of the circle (angle Pi), the point (-1, 0) corresponds to cos(Pi) = -1 and sin(Pi) = 0.
  • πŸ”„ The unit circle repeats every 2Pi radians, so 0 and 2Pi represent the same point.
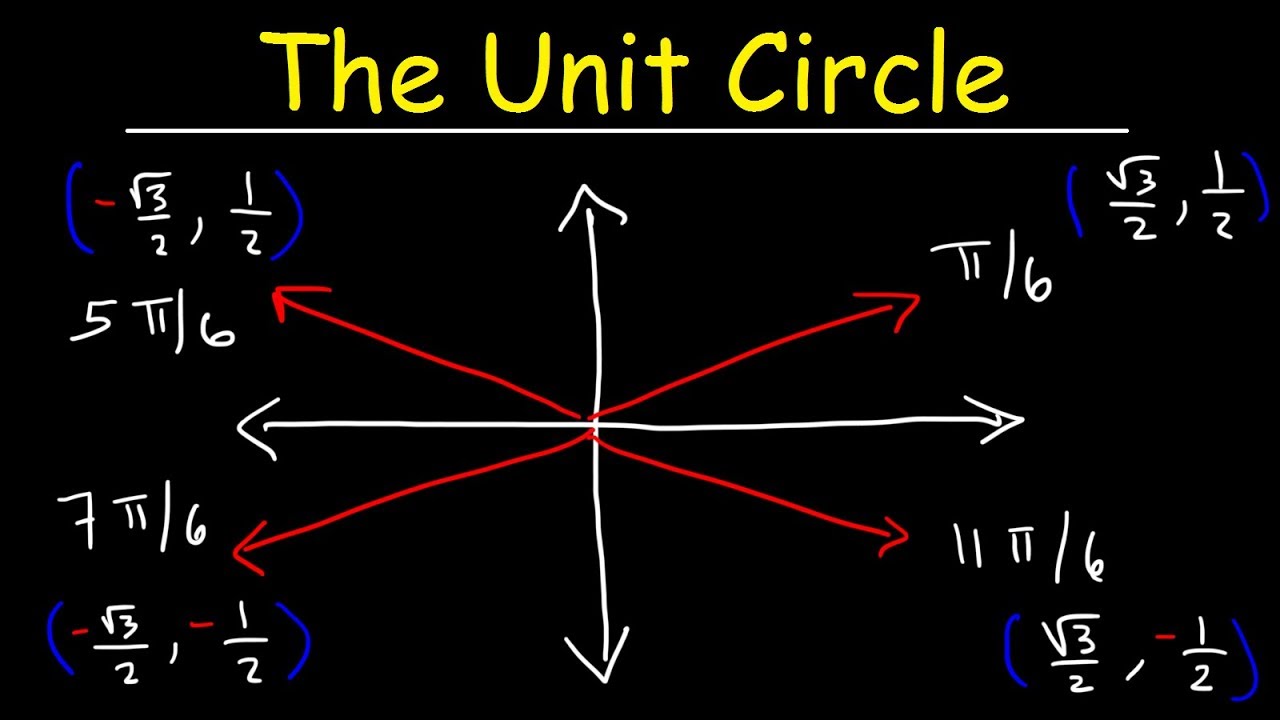
  • πŸ”’ For Pi/6, the point has an x-coordinate of sqrt(3)/2 and a y-coordinate of 1/2.
  • πŸ”„ Quadrants affect the sign of the coordinates: first quadrant is (+, +), second is (-, +), third is (-, -), and fourth is (+, -).
Q & A

  • What is the unit circle in trigonometry?

    -The unit circle is a circle with a radius of one, used in trigonometry to define the values of sine and cosine for various angles.

  • How do you start finding an angle on the unit circle?

    -You start on the right side of the unit circle and move up, rotating counter-clockwise to get to the desired angles.

  • What are the four main angles you get when dividing the unit circle by quarters?

    -The four main angles are 0 (or 2Ο€), Ο€/2, Ο€, and 3Ο€/2, each corresponding to a quarter of the circle.

  • What is the significance of the Pi/4 angles in the unit circle?

    -The Pi/4 angles divide the unit circle into eighths and are centered in the middle of each quarter of the circle, providing intermediate points between the main quarter angles.

  • What is the pattern for the x and y coordinates of the points on the unit circle?

    -The first coordinate (x) represents the cosine of the angle, and the second coordinate (y) represents the sine. The values depend on the quadrant and the specific angle, involving fractions, square roots, and sometimes negative signs.

  • What are the three key values to remember for the coordinates on the unit circle?

    -The three key values are 1/2 (the smallest), sqrt(2)/2 (the middle size), and sqrt(3)/2 (the largest), which are used for the x and y coordinates depending on the angle's position on the unit circle.

  • How do the signs of the coordinates change as you move through the quadrants of the unit circle?

    -In the first quadrant, all coordinates are positive. In the second quadrant, x is negative and y remains positive. In the third quadrant, both x and y are negative. In the fourth quadrant, x is positive and y is negative.

  • What is the conversion between radians and degrees for the angles on the unit circle?

    -Pi radians is equal to 180 degrees. Therefore, Ο€/2 radians is 90 degrees, Ο€/6 is 30 degrees, Ο€/4 is 45 degrees, Ο€/3 is 60 degrees, and so on.

  • How can you use the unit circle to find the cosine and sine values for a given angle?

    -Each point where an angle intersects the unit circle has an (x, y) coordinate. The x-coordinate represents the cosine value, and the y-coordinate represents the sine value for that angle.

  • What advice is given in the script for memorizing the unit circle?

    -The key to memorizing the unit circle is to recognize and remember the patterns in the angles and their corresponding coordinates, as well as understanding how the signs change with the quadrants.

  • Why is the unit circle considered a necessary tool in trigonometry?

    -The unit circle is considered necessary in trigonometry because it provides a visual and intuitive way to understand and remember the sine and cosine values for various angles, which are fundamental in solving trigonometric problems.

Outlines
00:00
πŸ“š Introduction to the Unit Circle

This paragraph introduces the concept of the unit circle in trigonometry, explaining that it is a circle with a radius of one. The speaker, Nancy, acknowledges the complexity of memorizing various angle values and sin and cos coordinates associated with the unit circle. However, she assures viewers that she will share patterns and tricks to aid in memorization. The unit circle is essential for understanding trigonometric functions, and Nancy begins by describing the axes and the four key points where the circle is touched by the x and y axes, corresponding to angles of 0, Pi/2, Pi, and 3Pi/2 radians. She emphasizes that angles are measured in radians, not degrees, and introduces the concept of a full circle being 2Pi radians.

05:04
πŸ“ Understanding Coordinates and Trigonometric Values

In this paragraph, Nancy delves deeper into the specifics of the unit circle by explaining the significance of the (x, y) coordinates of points where the circle is intersected by angles. She clarifies that the first coordinate (x) represents the cosine of the angle, and the second coordinate (y) represents the sine. Using the angle of 0 as an example, Nancy shows that the coordinates (1, 0) correspond to a cosine of 1 and a sine of 0. She then moves on to describe the coordinates for angles Pi/2, Pi, and 3Pi/2, highlighting the changes in the signs of the coordinates as one moves around the circle. Nancy also introduces the concept of dividing the circle into smaller parts to find the coordinates for angles like Pi/6, Pi/4, and Pi/3, emphasizing the importance of the numbers 1/2, sqrt(2)/2, and sqrt(3)/2 in these calculations.

10:11
🌐 Applying the Unit Circle to Trigonometry

This paragraph focuses on the practical application of the unit circle in determining the trigonometric values for various angles. Nancy explains how each angle on the unit circle corresponds to a unique point with an (x, y) coordinate that provides the cosine and sine values for that angle. She provides a method for determining these values by considering the quadrant in which the angle lies and the patterns observed in the coordinates. Nancy also touches on the conversion between radians and degrees, offering equivalents for the radian angles discussed earlier in the video. She concludes by encouraging viewers to focus on the patterns of the unit circle to make learning and memorization easier, and reminds them that while the unit circle may seem daunting, it is a fundamental tool in understanding trigonometry.

Mindmap
Keywords
πŸ’‘Unit Circle
The unit circle is a circle with a radius of one, centered at the origin of the coordinate plane. It is a fundamental concept in trigonometry as it helps in understanding the relationships between angles and their sine and cosine values. In the video, the unit circle is introduced as a necessary tool for memorizing trigonometric values, with the presenter explaining how angles on the unit circle correspond to specific points on the coordinate plane, which in turn provide the values for sine and cosine functions.
πŸ’‘Trigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. It is widely used in various fields, including physics, engineering, and navigation. In the context of the video, trigonometry is the focus of the lesson, with the unit circle being a key tool for understanding and memorizing the sine and cosine values of different angles.
πŸ’‘Sine (sin)
In trigonometry, the sine of an angle is a function that relates the ratio of the length of the side opposite the angle to the length of the hypotenuse in a right-angled triangle. The video emphasizes the importance of the unit circle in determining the sine values for various angles, with the y-coordinate of the point where the angle intersects the unit circle representing the sine value.
πŸ’‘Cosine (cos)
Cosine is another trigonometric function that represents the ratio of the length of the adjacent side to the length of the hypotenuse in a right-angled triangle. In the video, the cosine values are derived from the x-coordinates of the points where angles intersect the unit circle. The presenter explains how to find the cosine values for different angles by looking at the horizontal distance from the origin to the point of intersection.
πŸ’‘Radians
Radians are a unit of measure used to express angles in mathematics, particularly in trigonometry. One radian is the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle. The video script emphasizes the use of radians over degrees when working with the unit circle, as angles on the unit circle are given in radians, such as Pi/2 for a 90-degree angle.
πŸ’‘Coordinates (x, y)
Coordinates, denoted as (x, y) in the context of the video, are pairs of numbers that specify a point's location on the two-dimensional coordinate plane. The x-coordinate represents the horizontal position, while the y-coordinate indicates the vertical position. In the unit circle, each angle corresponds to a point with specific x and y coordinates that provide the values for the cosine and sine of that angle.
πŸ’‘Quadrants
The quadrants are the four equal regions of the coordinate plane formed by the intersection of the x-axis and y-axis. Each quadrant is defined by the signs of the x and y coordinates of the points within it. In the video, the unit circle is used to explain how angles in different quadrants result in positive or negative x and y coordinates, which in turn affect the signs of the cosine and sine values.
πŸ’‘Patterns
Patterns in the context of the video refer to the recurring sequences of numbers that help in memorizing the sine and cosine values for angles on the unit circle. The presenter highlights the importance of recognizing these patterns, such as the sequence 1, 3, 5, 7 for the angles Pi/4, Pi/2, 3Pi/2, and 2Pi, and the use of fractions and square roots for the values of sine and cosine.
πŸ’‘Negative Signs
Negative signs in the context of the unit circle indicate the quadrant in which a particular angle lies, affecting the signs of the cosine and sine values. The video explains how the signs of the coordinates change as you move from one quadrant to another, with negative signs appearing in the second, third, and fourth quadrants.
πŸ’‘Degrees
Degrees are a unit of measurement for angles, with a full circle being 360 degrees. While the video primarily works with radian measures, it also mentions the conversion to degrees, which is another way to express angles. The relationship between radians and degrees is established by the fact that Pi radians is equal to 180 degrees.
πŸ’‘Memorization
Memorization is the process of committing information to memory, which is essential in learning various mathematical concepts, including trigonometry. The video aims to help viewers memorize the unit circle and the corresponding sine and cosine values for different angles by identifying patterns and using the visual aid of the unit circle.
Highlights

The unit circle is a circle with a radius of one.

Memorizing the unit circle is essential in trigonometry due to its numerous angle values and sin and cos coordinates.

The unit circle is divided into four main angles by the x and y axes, starting from the right and moving counter-clockwise.

The angles on the unit circle are measured in radians, with 0, Pi/2, Pi, 3Pi/2, and 2Pi representing the angles at the four points where the axes touch the circle.

The pattern of angles in the unit circle is based on dividing the circle into quarters and then further subdividing these quarters.

The angles Pi/4, Pi/6, and Pi/3 are derived from dividing the quadrants and are centered in each quadrant.

The x and y coordinates of the points where the angles touch the unit circle correspond to the cos and sin values of those angles.

For an angle of 0, the (x, y) coordinates are (1, 0), making the cos 1 and the sin 0.

At Pi/2, the (x, y) coordinates are (0, 1), with a cos of 0 and a sin of 1.

The (x, y) coordinates for the left side of the unit circle at Pi are (-1, 0), and for the bottom at 3Pi/2, they are (0, -1).

The values 1/2, sqrt(2)/2, and sqrt(3)/2 are fundamental for the x-coordinates of the points at angles Pi/6, Pi/4, and Pi/3, respectively.

The y-coordinates follow the same pattern as the x-coordinates, with the smallest being 1/2, the middle being sqrt(2)/2, and the largest being sqrt(3)/2.

The sign of the coordinates changes depending on the quadrant, with positive x and y in the first quadrant, negative x and positive y in the second, negative x and y in the third, and positive x and negative y in the fourth.

The unit circle can be used to find the cos and sin values for any angle, with the first value in the (x, y) point being the cos and the second being the sin.

The angles Pi/6, Pi/4, and Pi/3 correspond to degree angles of 30, 45, and 60 degrees respectively.

Memorizing the patterns in the unit circle is key to learning it effectively and efficiently.

The video provides a comprehensive guide to understanding and memorizing the unit circle for trigonometry.

Transcripts

Browse More Related Video

The Unit Circle, Basic Introduction, Trigonometry

Trig 0.2 - Trig Functions Defined on the Unit Circle

Unit Circle Definition of Trig Functions

Trig Visualized: One Diagram to Rule them All (six trig functions in one diagram)

30-60-90 Triangles - Special Right Triangle Trigonometry

Even and Odd Trigonometric Functions & Identities - Evaluating Sine, Cosine, & Tangent

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryMath HelpUnit CircleEducationalMath TricksStudy GuideLearning MathRadian AnglesMath TutorialHigh School Math