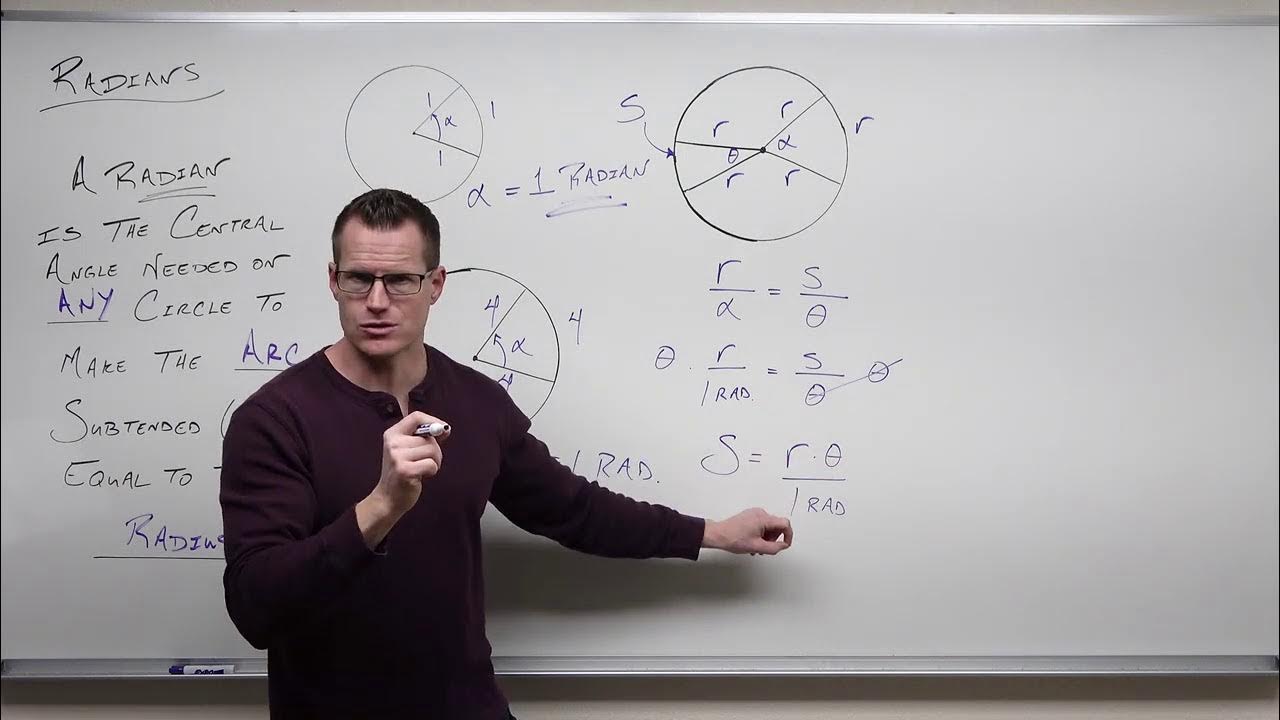CONVERTING DEGREE MEASURE TO RADIAN MEASURE AND VICE VERSA || PRE-CALCULUS

WOW MATH

25 Nov 202109:41

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video lesson by Mark Awamat focuses on converting between degree and radian measures. It explains that one radian is the measure of a central angle subtended by an arc equal to the radius of the circle, with the circumference being 2πr radians. The video clarifies that 2π radians is equivalent to 360 degrees, simplifying the conversion process. It demonstrates how to convert angles from degrees to radians and vice versa, using mathematical examples to illustrate the steps involved. The lesson is designed to help viewers understand and perform these conversions with ease, making it an informative resource for those studying trigonometry.

Takeaways

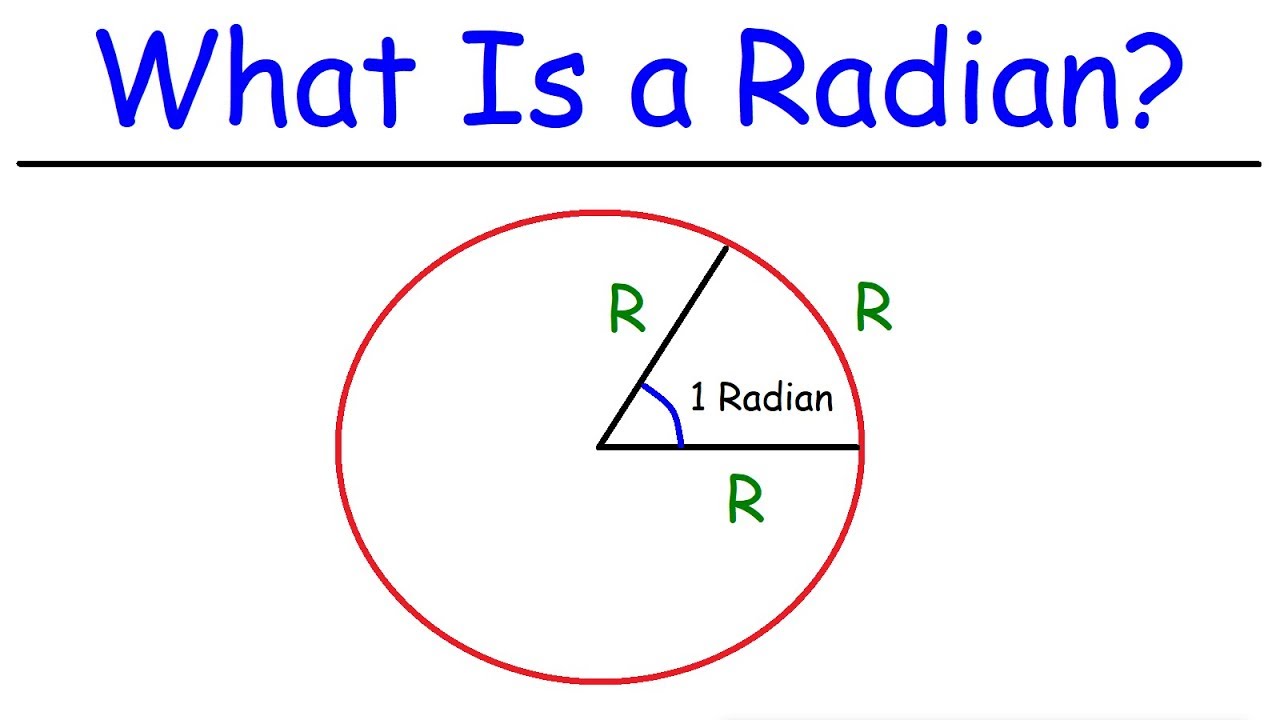
📐 The term 'radian' is used to measure angles in the context of a circle, where one radian is the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle.
🔴 One full circle is equivalent to 2π radians, which is the same as the circumference of the circle (2πr).
⭕ The circumference of a circle is calculated as 2π times the radius (r), which is also equal to 2π radians.
🔄 Two pi radians (2π) is equal to 360 degrees, which is the total angle measure of a circle.
🔢 The conversion from radians to degrees is done by multiplying the number of radians by 180 and dividing by π (pi).
↔️ Conversely, to convert from degrees to radians, multiply the number of degrees by π (pi) and divide by 180.
🧮 An example conversion from radians to degrees is shown with 5π/3 radians, which equals 300 degrees.
📉 Another example is -7π/6 radians, which converts to -210 degrees.
✅ The greatest common factor (GCF) is used in the conversion process to simplify calculations.
💡 The script provides an alternative solution for conversion by using the known equivalence of π to 180 degrees.
📚 The video is an educational resource for learning how to convert between degrees and radians, which is a fundamental concept in mathematics, particularly in geometry and trigonometry.
📈 The importance of understanding radian measure is highlighted, as it is widely used in calculus and other advanced mathematical fields.

Q & A

What is the relationship between a circle's circumference and its radius in terms of radian measure?
-The circumference of a circle is related to its radius by the formula 2πr, where r is the radius of the circle. In radian measure, this is equivalent to 2π radians since one radian is the measure of a central angle subtended by an arc equal to the radius of the circle.
How is the term 'radian' defined in the context of the video?
-A radian is defined as the measure of a central angle subtended by an arc of a circle that is equal to the radius of the circle. It is a unit of angular measure where one radian is the angle subtended at the center of a circle by an arc equal in length to the radius of the circle.
What is the conversion factor between radians and degrees?
-The conversion factor between radians and degrees is that 2π radians is equal to 360 degrees. This means that π radians is equal to 180 degrees, and thus one degree is equal to π/180 radians.
How can you convert an angle measured in radians to degrees?
-To convert an angle from radians to degrees, you multiply the number of radians by 180 degrees and then divide by π. For example, to convert 5π/3 radians to degrees, you would calculate (5π/3) * (180/π) which simplifies to 300 degrees.
What is the process of converting degrees to radians?
-To convert degrees to radians, you multiply the number of degrees by π and then divide by 180. This is because one degree is equal to π/180 radians.
What is the radian measure of a full circle?
-A full circle has an angle measure of 360 degrees, which is equivalent to 2π radians.
How many degrees are in one radian?
-One radian is equivalent to 180 degrees divided by π, which is approximately 57.2958 degrees.
Can you provide an example of converting 3π radians to degrees?
-To convert 3π radians to degrees, you would multiply 3π by 180 degrees and divide by π, which results in 3 * 180 degrees / π = 540 degrees.
What is the radian measure equivalent to 75 degrees?
-To find the radian measure equivalent to 75 degrees, you multiply 75 by π/180, which results in (75 * π) / 180 = 5π/12 radians.
How would you convert -210 degrees to radians?
-To convert -210 degrees to radians, you multiply -210 by π/180. This results in -210 * π / 180 = -7π/6 radians.
What is the significance of the circle net in understanding radians?
-A circle net is a representation of a circle's circumference laid out flat. It helps in understanding the concept of radians by showing that the circumference of a circle, which is 2πr, can be represented as 2π radians, where r is the radius.

Outlines

00:00

📚 Introduction to Degree and Radian Conversion

In this video lesson, Mark Awamat introduces the concept of converting between degree and radian measures. He explains that one radian is the measure of a central angle subtended by an arc of a circle that is equal to the radius of the circle. Using the circumference of a circle, which is 2πr, he demonstrates that one radian is equivalent to the circumference divided by the radius, simplifying to 2π radians. He then relates radians to degrees, stating that 2π radians equal 360 degrees. He further breaks down the conversion by showing that π radians is equivalent to 180 degrees, leading to the conversion formula where one degree equals π/180 radians. The lesson continues with examples of converting angles from degrees to radians and vice versa using multiplication and simplification techniques.

05:00

🔍 Detailed Examples of Degree and Radian Conversions

This paragraph delves into detailed examples of converting radian measures to degree measures and vice versa. The instructor provides step-by-step solutions for converting various radian measures, such as 5π/3, 3π, and -7π/6, into their corresponding degree measures. He uses the formula for conversion, multiplying the radian measure by 180 degrees and dividing by π, then simplifying the result. The examples include both positive and negative radian values, illustrating how to handle different scenarios. Additionally, the instructor offers alternative solutions by using the equivalence of 180 degrees to π and simplifying the calculations accordingly. The paragraph concludes with a brief mention of converting degree measures to radian measures, using the formula π/180, and provides examples such as 225 degrees and -210 degrees being converted to radian measures. The video aims to equip viewers with a clear understanding of angle measure conversions in trigonometry.

Mindmap

Keywords

💡Degree Measure

Degree measure refers to the unit of angular measurement used in the context of geometry. It is defined as 1/360th of a full circle. In the video, degree measure is used to compare and convert angles to radians, which is another unit of angular measurement. For example, the script mentions that 'two pi radians is equal to 360 degrees', illustrating the relationship between radians and degrees.

💡Radian Measure

Radian measure is an alternative unit for measuring angles, often used in calculus and advanced mathematics. It is defined as the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle. The video explains that 'one radian is equivalent to 180 degrees over pi', providing a conversion factor between radians and degrees.

💡Central Angle

A central angle is an angle whose vertex is at the center of a circle and whose sides pass through two points on the circumference of the circle. The video uses the concept of a central angle to explain the relationship between the circumference of a circle and the measure of an angle in radians, stating that 'one radian is the measure of a central angle subtended by an arc of a circle that is equal to the radius of the circle'.

💡Circumference

Circumference is the total length of the edge of a circle or ellipse. In the video, the circumference is related to the concept of radians, with the statement that 'the circumference of a circle is two pi r', where 'r' is the radius of the circle. This relationship is used to establish the equivalence of two pi radians to the full circumference.

💡Radius

The radius of a circle is the distance from the center of the circle to any point on its circumference. The video script uses the radius in the formula for the circumference of a circle, 'two pi r', and in the conversion between radians and degrees, such as 'one radian is equivalent to 180 degrees over pi'.

💡Conversion

Conversion in the context of the video refers to the process of changing one unit of measurement to another. The script provides methods for converting between degree measures and radian measures. For instance, it explains that 'to convert from degrees to radians, multiply the number of degrees by pi over 180'.

💡Pi (π)

Pi, often denoted as 'π', is a mathematical constant representing the ratio of a circle's circumference to its diameter. The video emphasizes pi's role in the conversion between degrees and radians, such as in the formula '180 degrees over pi' to convert degrees to radians.

💡Arc

An arc is a portion of the circumference of a circle. In the video, the arc is used to define the measure of a radian, as it states that 'one radian is the measure of a central angle subtended by an arc of a circle that is equal to the radius of the circle'.

💡Greatest Common Factor (GCF)

The greatest common factor, or GCF, is the largest number that divides two or more numbers without leaving a remainder. In the video, the GCF is used in the conversion process to simplify fractions when converting between degrees and radians, as seen in the example where '180 degrees over pi' is simplified by dividing both the numerator and the denominator by their GCF.

💡Illustration

Illustration in this context refers to a visual representation or diagram used to aid understanding. The video mentions an 'illustration' to help viewers visualize the concepts being discussed, such as the relationship between the central angle, arc, and radius of a circle.

💡Tutorial

A tutorial is an instructional video or lesson designed to teach a specific skill or concept. The video script is part of a tutorial series aimed at teaching math lessons, specifically focusing on converting between degree and radian measures in this instance.

Highlights

The video lesson discusses converting degree measure to radian measure and vice versa.

One radian is the measure of a central angle subtended by an arc of a circle that is equal to the radius of the circle.

The circumference of a circle is 2πr, where r is the radius.

A full circle in radian measure is 2π radians.

If the radius of a circle is 1, then the circumference is 2π radians.

A circle subtends an angle of 360 degrees.

2π radians is equal to 360 degrees.

π radians is equivalent to 180 degrees.

One radian is equivalent to 180 degrees over π.

To convert from degrees to radians, multiply the number of degrees by π/180.

To convert from radians to degrees, multiply the number of radians by 180/π.

Example: Convert 5π/3 radians to degree measure.

The answer for 5π/3 radians is 300 degrees.

Example: Convert 3π radians to degree measure.

The answer for 3π radians is 540 degrees.

Example: Convert -7π/6 radians to degree measure.

The answer for -7π/6 radians is -210 degrees.

Example: Convert 225 degrees to radian measure.

The answer for 225 degrees is 5π/4 radians.

Example: Convert 75 degrees to radian measure.

The answer for 75 degrees is 5π/12 radians.

Example: Convert -210 degrees to radian measure.

The answer for -210 degrees is -7π/6 radians.

The video concludes with a recap on how to convert angles' measures from degrees to radians and radians to degrees.

Transcripts

Browse More Related Video

Introduction to Trigonometry: Angles and Radians

Converting Radians and Degrees (Precalculus - Trigonometry 4)

Trigonometry - What Exactly Is a Radian?

Radians and Degrees

Trig 0.1 - Angles, Degrees and Radians

Introduction to Radians (Precalculus - Trigonometry 3)

CONVERTING DEGREE MEASURE TO RADIAN MEASURE AND VICE VERSA || PRE-CALCULUS

Takeaways

Q & A

What is the relationship between a circle's circumference and its radius in terms of radian measure?

How is the term 'radian' defined in the context of the video?

What is the conversion factor between radians and degrees?

How can you convert an angle measured in radians to degrees?

What is the process of converting degrees to radians?

What is the radian measure of a full circle?

How many degrees are in one radian?

Can you provide an example of converting 3π radians to degrees?

What is the radian measure equivalent to 75 degrees?

How would you convert -210 degrees to radians?

What is the significance of the circle net in understanding radians?