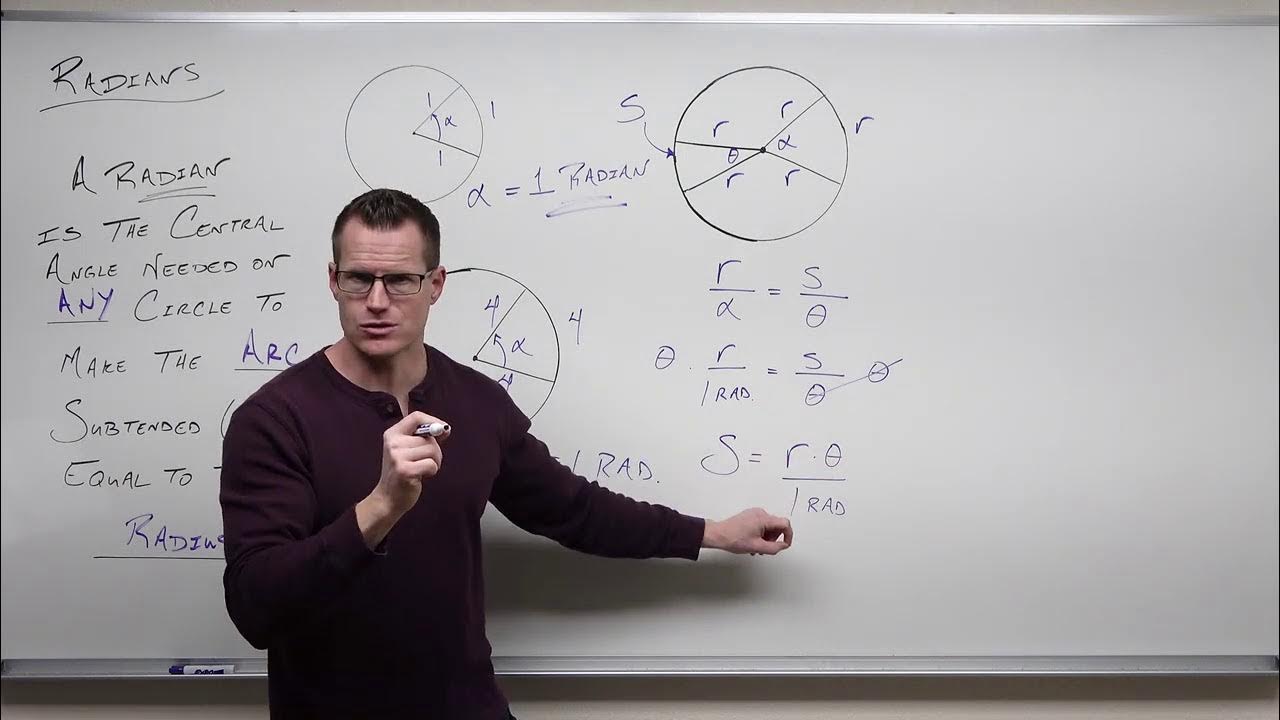Converting Radians and Degrees (Precalculus - Trigonometry 4)

Professor Leonard

18 Feb 202138:45

EducationalLearning

32 Likes 10 Comments

TLDRThis video script delves into the importance of understanding and converting between degrees and radians, two fundamental units of angular measurement. The presenter emphasizes the significance of both units in real-life applications and mathematical formulas. The script begins with a review of radians, explaining them as the angle required to sweep out an arc length equal to the circle's radius. It then explores the relationship between radians and the circle's circumference, which is 2πr, and how this relationship leads to the common presence of π in radian measurements. The video provides a clear conversion method between degrees and radians, highlighting that one full circle is 2π radians or 360 degrees. Several examples are given to illustrate the conversion process in both directions, emphasizing the mathematical reasoning behind each step. The script also introduces the concept of a unit circle in both degrees and radians, helping viewers to visualize and understand the correlation between the two measurement systems. The presenter uses creative strategies, such as cutting a straight angle into parts and counting them, to help viewers grasp the concept intuitively. The goal is to ensure viewers are comfortable with both units and can navigate between them with ease, preparing them for future mathematical endeavors.

Takeaways

📐 **Radians vs. Degrees**: Understanding the difference between radians and degrees is crucial as both are used in various mathematical and real-life applications.
🔄 **Conversion Fundamentals**: One full circle is 2π radians, which is equivalent to 360 degrees, providing a basis for converting between the two units.
🔢 **Conversion Formulas**: To convert degrees to radians, multiply the degree measure by π/180. Conversely, to convert radians to degrees, multiply the radian measure by 180/π.
📉 **Arc Length and Central Angle**: The arc length is proportional to the central angle that cuts it, with the formula arc length = radius × angle (in radians).
🈵 **Full Rotation**: A full rotation (360 degrees) is equivalent to 2π radians, which is a key concept in understanding the relationship between radians and the circle's circumference.
🔴 **Radians and the Circle's Circumference**: The reason radians often include π is due to the circle's circumference being 2π times the radius.
🤔 **Understanding Quadrants**: Radians and degrees can be used to identify the quadrant in which an angle lies, which is essential for applications like trigonometry.
➗ **Simplification**: When converting between radians and degrees, simplification of fractions is often necessary to find the most straightforward representation of the angle.
⛓ **Negative Angles**: Negative angles in both radians and degrees represent rotation in the clockwise direction and can be converted using the same principles as positive angles.
🔺 **Common Radian Values**: Familiarize yourself with common radian values like π/3, π/2, and 2π, as they relate to specific angles in degrees and are frequently used in calculations.
🧮 **Decimal Approximations**: When exact simplification is not possible, using decimal approximations for π is acceptable, especially when using a calculator for precise conversions.

Q & A

What are radians and why are they important in mathematics?
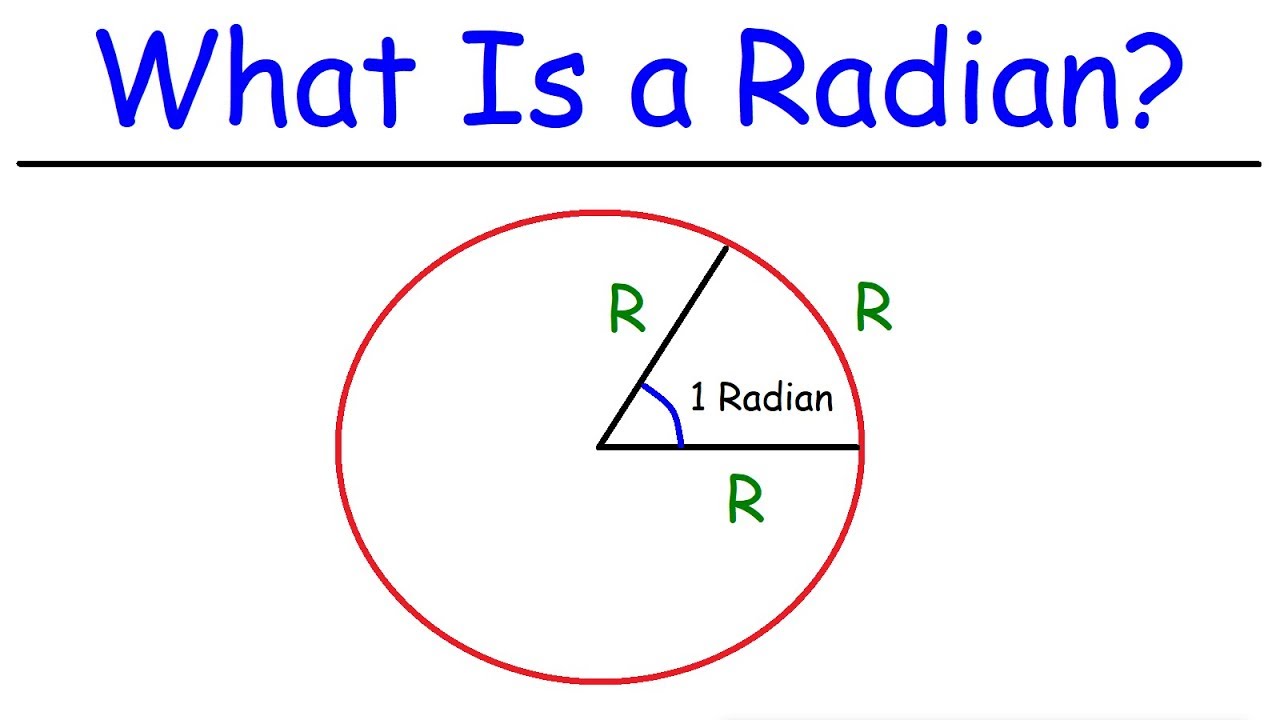
-Radians are a unit of angular measure where one radian is the angle that, at the center of a circle, subtends an arc whose length is equal to the radius of the circle. They are important in mathematics because many mathematical formulas, especially those involving calculus and trigonometry, are defined in terms of radians.
How do you convert between degrees and radians?
-You can convert between degrees and radians using the relationship that one full rotation (360 degrees) is equivalent to 2π radians. To convert degrees to radians, multiply the number of degrees by π and then divide by 180. To convert radians to degrees, multiply the number of radians by 180 and then divide by π.
Why do radians often involve the number π in their measurements?
-Radians often involve π because the circumference of a circle, which is 2π times the radius, is the basis for the definition of a radian. When measuring angles in radians, you are essentially measuring a fraction of the circle's circumference.
What is the relationship between the arc length of a circle and the central angle in radians?
-The arc length of a circle is proportional to the central angle in radians. Specifically, the arc length (s) is equal to the radius (r) multiplied by the central angle (θ) in radians (s = r * θ).
How is the concept of a unit circle used in understanding angles in both degrees and radians?
-A unit circle is a circle with a radius of 1. It is used to understand angles by measuring how far a point on the circle travels as it rotates around the circle. In degrees, the unit circle helps visualize angles from 0 to 360 degrees. In radians, it helps visualize angles from 0 to 2π radians, with each quadrant corresponding to a specific range of radians.
What is the conversion factor from degrees to radians for one degree?
-The conversion factor from degrees to radians for one degree is π/180 radians. This means that each degree is equivalent to π/180 of a full circle.
How many radians are in a full circle?
-A full circle is 2π radians. This is derived from the fact that the circumference of a circle is 2π times the radius, and a full circle represents a complete arc length equal to the circumference.
What is the relationship between the circumference of a circle and radians?
-The circumference of a circle, which is 2π times the radius (r), is directly related to radians because the arc length that corresponds to a full circle (360 degrees) is equal to the circumference. Therefore, one full rotation (2π radians) corresponds to the circumference of the circle.
What is the quadrant angle in radians that corresponds to 90 degrees?
-The quadrant angle in radians that corresponds to 90 degrees is π/2 radians. This is because 90 degrees is one-fourth of a full circle, and since a full circle is 2π radians, one-fourth of that would be π/2 radians.
How can you determine the quadrant of an angle in radians?
-To determine the quadrant of an angle in radians, consider the value of the angle in relation to π. An angle between 0 and π/2 radians is in the first quadrant. Between π/2 and π radians is in the second quadrant. Between π and 3π/2 radians is in the third quadrant, and between 3π/2 and 2π radians is in the fourth quadrant.
What is the conversion from radians to degrees for a negative angle?
-The conversion from radians to degrees for a negative angle is the same as for a positive angle. You use the conversion factor 180 degrees over π to find the equivalent angle in degrees. The sign (positive or negative) indicates the direction of rotation, with positive being counterclockwise and negative being clockwise.

Outlines

00:00

😀 Introduction to Radians and Degrees Conversion

The video begins by welcoming viewers and hoping they have watched the previous video on radians. It emphasizes the importance of understanding radians and degrees, as both are crucial in real-life applications and mathematical formulas. The speaker intends to teach the conversion between these two units of angle measurement and explains the concept of a radian as the angle that corresponds to an arc length equal to the radius of a circle. The video also mentions the prevalence of pi in radian measurements and promises to explore why this is the case.

05:01

📐 Understanding the Relationship Between Arc Length and Central Angle

The speaker delves into the relationship between arc length and the central angle that cuts it. Using the formula that arc length equals radius times theta (in radians), the video explains that when a full rotation is made, the arc length equals the circumference of the circle. The circumference is given as 2 pi r, leading to the conclusion that two pi radians make up a full circle. This understanding is crucial for converting between radians and degrees and is foundational for the rest of the video's content.

10:01

🔄 Conversion Between Radians and Degrees

The video explains the conversion between radians and degrees by establishing that one full revolution of a circle is 360 degrees and also equals two pi radians. This equivalence allows for the conversion formula where one degree is equal to pi over 180 radians. The video also shows the reverse conversion, with one radian being equal to 180 degrees over pi. The speaker reinforces the idea that radians and degrees are interchangeable and emphasizes the importance of memorizing these relationships for mathematical and real-life applications.

15:03

🤔 Grasping the Concept of Unit Circles in Degrees and Radians

The speaker introduces the concept of unit circles, explaining how they are represented in both degrees and radians. The video discusses how angles are measured on the coordinate system and how these measurements correspond to positions on the unit circle. It also covers how to determine the quadrant in which an angle lies, whether measured in degrees or radians, and highlights the importance of understanding these concepts for future mathematical studies.

20:04

🔢 Converting Between Degrees and Radians with Examples

The video provides examples of converting angles from degrees to radians and vice versa. It demonstrates how to use the conversion formulas and emphasizes the importance of understanding the quadrant in which the angle lies. The speaker simplifies the process by using the straight angle of pi and the concept of cutting and counting parts of this angle to determine the equivalent in radians or degrees. The video also touches on the challenges of converting angles that do not simplify nicely and suggests using decimals in such cases.

25:06

🤓 Advanced Conversion Techniques and Applications

The video concludes with more complex examples of angle conversion, including angles that represent more than one full rotation. The speaker shows how to handle such conversions and how to determine the correct quadrant for the angle. It also briefly mentions the use of radians in mathematical formulas and the importance of being comfortable with both radians and degrees for future studies and real-world applications. The video ends on a positive note, encouraging viewers to apply these concepts in real-life scenarios.

30:06

🎓 Summary of Key Concepts and Final Thoughts

In the final paragraph, the speaker summarizes the key concepts discussed in the video, including the relationship between the circumference of a circle and radians, as well as the conversion between radians and degrees. The video emphasizes the importance of understanding where these measurements come from and how they are applied. The speaker expresses hope that the explanations provided have been clear and helpful, and that viewers are ready to tackle real-life examples in future videos.

Mindmap

Keywords

💡Radians

Radians are a unit of angular measure where the angle is proportional to the arc length it subtends on a unit circle. In the video, radians are used to explain how angles can be measured in relation to the circumference of a circle, with the full circumference being 2π radians. An example from the script is 'two pi radians in one rotation of a circle', which helps to understand the conversion between radians and degrees.

💡Degrees

Degrees are a common unit of angular measurement where a full circle is divided into 360 equal parts. The video emphasizes the importance of understanding both degrees and radians for various mathematical and real-life applications. The script mentions 'one full revolution circle is 360 degrees', highlighting the standard definition and comparison to radians.

💡Arc Length

Arc length refers to the distance along a curve, in this case, a part of the circumference of a circle. The video discusses the relationship between arc length and the central angle in radians that subtends it, which is key to converting between radians and degrees. An example used is 'arc length equals radius times theta', where theta is the central angle in radians.

💡Circumference

The circumference of a circle is the total length of the circle's edge and is given by the formula 2πr, where r is the radius of the circle. The video explains that the circumference is fundamental to understanding radians, as it is the full arc length that a central angle of two pi radians subtends. 'Circumference of a circle is 2 pi r' is a phrase used in the script to illustrate this concept.

💡Central Angle

A central angle is an angle whose vertex is at the center of a circle and whose sides pass through two points on the circle. The video uses the concept of the central angle to explain the relationship between radians and the arc length on a circle. It is mentioned in the context of 'the central angle that terminates the radius where it initiated', which is pivotal for understanding the conversion formula.

💡Unit Circle

A unit circle is a circle with a radius of 1 unit. The video introduces the concept of a unit circle in both degrees and radians, which is a fundamental tool in trigonometry. The script discusses how angles in radians and degrees can be visualized on a unit circle, with examples like '90 degrees and pi over 2 mean the same thing', which refers to their equivalence on a unit circle.

💡Conversion

The process of converting from one unit of measure to another is a key focus of the video. The script provides the formula 'one degree is equal to π/180 radians' and its inverse to show how to convert between degrees and radians. The conversion is crucial for mathematical consistency and is demonstrated with various examples throughout the video.

💡Proportion

Proportion refers to the relationship of two quantities in mathematics, often in the form of ratios or fractions. In the context of the video, the concept of proportion is used to explain why radians are part of the formula for arc length and how the full circumference of a circle relates to a full rotation in radians. The script mentions 'arc length is proportionally related to the central angle that cuts it', which is a fundamental principle in the discussion.

💡Trigonometry

Trigonometry is the branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. The video is centered around the application of trigonometry, specifically the use of radians and degrees in the context of a unit circle. Trigonometry is implicitly referenced through the discussion of angles and their measurements in relation to circles.

💡Quadrants

Quadrants are the four equal parts into which a plane is divided by the two axes in a Cartesian coordinate system. The video explains how angles measured in degrees and radians correspond to different quadrants on a unit circle. The script uses quadrants to describe the position of angles such as '60 degrees is somewhere between 0 and 90 closer to the 90', which places it in the first quadrant.

💡Reference Angle

A reference angle is the acute angle that could be used to describe any general angle's position in relation to the x-axis on a unit circle. The video discusses reference angles in the context of negative angles and how they can be used to determine the quadrant of an angle. An example from the script is 'negative 135 degrees', which is explained as being in the third quadrant, using the concept of a reference angle.

Highlights

The importance of understanding both degrees and radians in measuring angles, as they are used frequently in various real-life applications.

The fundamental concept of radians, which is the angle needed to sweep out an arc length equal to the radius on the center of a circle.

The relationship between arc length and central angle in radians, which is expressed by the formula arc length = radius * theta.

The fact that a full rotation or one complete circle is equivalent to 2 pi radians, providing a basis for converting between radians and degrees.

The conversion formula between degrees and radians: 1 degree = pi/180 radians and 1 radian = 180/π degrees.

The significance of pi in radians, which stems from the proportion of the circle's circumference (2 pi r) in relation to the arc length.

The concept of unit circles, which are used to visualize and understand angles in both degrees and radians.

The quadrant angles in both degree and radian measurements, emphasizing that 90 degrees is equivalent to pi/2 radians, and so on for other quadrant angles.

The method of converting from degrees to radians using the formula and understanding the simplification process, such as converting 60 degrees to pi/3 radians.

The explanation of how to visualize and understand the conversion of negative angles from degrees to radians, such as negative 45 degrees to -pi/4 radians.

The process of converting radians to degrees, demonstrated by converting pi/6 radians to 30 degrees and explaining the quadrant placement for each.

The demonstration of converting more complex radian measurements to degrees, such as 7 pi/3 radians to approximately 420 degrees, and understanding their quadrant locations.

The challenge of converting radians without pi in them, like 4 radians, and the method of using decimal approximations for degrees, resulting in approximately 229.18 degrees.

The emphasis on the importance of understanding the interplay between the circumference of a circle and the use of pi in radians, as well as the ability to convert between the two units of angle measurement.

The practical approach to learning and understanding the conversions between degrees and radians, using visualization and memorization techniques for better comprehension.

Transcripts

Browse More Related Video

Introduction to Radians (Precalculus - Trigonometry 3)

CONVERTING DEGREE MEASURE TO RADIAN MEASURE AND VICE VERSA || PRE-CALCULUS

Trig 0.1 - Angles, Degrees and Radians

Radians and Degrees

Introduction to Trigonometry: Angles and Radians

Arc Length of a Circle Formula - Sector Area, Examples, Radians, In Terms of Pi, Trigonometry

Related Tags

Math Conversion Degrees to Radians Radians to Degrees Circle Geometry Trigonometry Unit Circle Arc Length Central Angle Circumference Proportional Relationship