Physics 20 - Manipulating kinematics formulas

NorQuest College - Online Anytime

31 May 202221:00

EducationalLearning

32 Likes 10 Comments

TLDRThis video script focuses on the manipulation of kinematic formulas to solve for various variables in physics problems. It emphasizes the importance of rearranging equations to isolate the desired variable and provides clear examples of how to do so with velocity, acceleration, and time. The script also highlights the significance of unit consistency throughout the problem-solving process, ensuring that the units on both sides of the equation match up correctly.

Takeaways

📚 Understanding and manipulating kinematic equations is essential for solving physics problems involving motion.
🔄 To rearrange formulas, perform the opposite operation; e.g., if you're dividing, multiply, and vice versa.
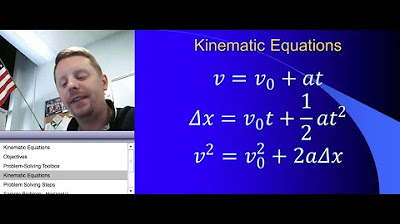
🏃‍♂️ The velocity formula (v = d/t) can be rearranged to solve for distance (d = vt) or time (t = d/v).
🕒 For acceleration (a = (vf - vi) / t), rearranging can help solve for time (t = (vf - vi) / a) or final velocity (vf = vi + at).
🔄 When solving for initial velocity (vi), manipulate the equation to isolate vi (vi = vf - at).
📈 The method of solving for different variables often involves combining operations such as addition, subtraction, multiplication, and division.
🤹‍♂️ Unit analysis is crucial when rearranging equations to ensure that the units on both sides of the equation are consistent.
📊 The script provides examples of how to solve for various variables within kinematic equations, emphasizing the importance of practice and understanding.
📐 The concept of average velocity is introduced, and its formula (v_avg = (vf + vi) / 2) is derived from the distance formula.
🚀 Practical applications of these formulas include calculating the time it takes for an object to fall from a certain height due to gravity.
🔧 When dealing with problems where the initial velocity is zero, the equations become simpler, allowing for easier calculations.

Q & A

What is the primary focus of the video?
-The primary focus of the video is to teach viewers how to manipulate and rearrange kinematics equations to solve for different variables.
What is the first formula discussed in the video?
-The first formula discussed is the formula for velocity, which is velocity equals distance over time (v = d/t).
How can you rearrange the velocity formula to solve for distance?
-To solve for distance, you can rearrange the velocity formula to d = v * t, by multiplying both sides of the equation by time.
What is the formula for time in terms of velocity and distance?
-The formula for time in terms of velocity and distance is t = d / v, which is obtained by multiplying both sides of the original velocity formula by the velocity and then dividing by the time.
How does the video explain the process of rearranging equations?
-The video explains that to rearrange equations, you need to do the opposite operation, such as multiplying when you want to isolate a variable that is divided by another on the other side of the equation.
What is the formula for acceleration discussed in the video?
-The formula for acceleration discussed is a = (vf - vi) / t, where a is acceleration, vf is final velocity, vi is initial velocity, and t is time.
How can you solve the acceleration formula for time?
-To solve the acceleration formula for time, you rearrange it to t = (vf - vi) / a, by multiplying both sides by t and then dividing by a.
What is the significance of the unit analysis mentioned in the video?
-The unit analysis is significant because it helps ensure that the units on both sides of the equation are consistent, which is necessary for the equation to be balanced and the solution to be valid.
How can you solve the distance formula for final velocity when the initial velocity is zero?
-When the initial velocity is zero, the distance formula simplifies to vf = d * a / (2 * t^2). This is derived by rearranging the formula to solve for vf and considering the case where vi is zero.
What is the application of the kinematics equations discussed in the video?
-The kinematics equations discussed in the video are applied to problems involving motion, such as calculating the time it takes for an object to fall from a certain height or determining the velocity of an object at a given time.

Outlines

00:00

📚 Manipulating Kinematics Equations

This paragraph introduces the concept of manipulating kinematics equations, specifically focusing on rearranging them to solve for different variables. The key kinematics equations from the data sheet are discussed, emphasizing the importance of being able to rearrange these formulas to solve for variables such as velocity, distance, and time. The video provides examples of how to manipulate the formulas for speed (velocity), time, and acceleration to isolate specific variables and solve related physics problems.

05:02

🔄 Rearranging Velocity and Time Equations

The paragraph delves into the process of rearranging the velocity and time equations to solve for different variables. It explains how to manipulate the formula for velocity (v = d/t) to find the distance (d = vt) and time (t = d/v). The process of isolating variables is demonstrated by using opposite operations, such as multiplying and dividing, to achieve the desired formula. The paragraph also covers how to solve for time in the context of acceleration, using the formula a = (vf - vi) / t and rearranging it to find t = (vf - vi) / a.

10:04

🚀 Solving for Final Velocity and Initial Velocity

This section focuses on solving the acceleration equation for final and initial velocities. It explains how to rearrange the equation to isolate the final velocity (vf = vi + at) and initial velocity (vi = vf - at). The explanation includes the process of adding and subtracting terms to both sides of the equation and the importance of understanding the relationship between final velocity, initial velocity, and acceleration. The paragraph also emphasizes the role of time in these calculations and how it affects the outcome.

15:04

📈 Deriving Average Velocity and Acceleration

The paragraph discusses the derivation of average velocity and acceleration from the given equations. It explains how to rearrange the distance formula to find the average velocity (d/t = vf + vi / 2) and how to solve for final velocity when the initial velocity is zero (vf = 2d / t - vi). The concept of average velocity is highlighted, and the importance of units consistency in solving physics problems is stressed. The paragraph also presents the method of solving for acceleration when the initial velocity is zero (a = 2d / t^2) and how to apply this in real-world scenarios, such as calculating the time it takes for an object to fall from a certain height.

20:05

🔢 Unit Analysis in Physics Equations

The final paragraph emphasizes the importance of unit analysis when manipulating and solving physics equations. It explains how to ensure that the units on both sides of the equation are consistent, which is crucial for obtaining accurate results. The paragraph provides examples of how to check the units for distance, velocity, and acceleration, and how they must correspond to maintain the equation's validity. The unit analysis is demonstrated using the acceleration equation, showing that the units of meters per second squared are maintained throughout the rearrangement process.

Mindmap

Keywords

💡Kinematics

Kinematics is the branch of physics that deals with the motion of objects without considering the forces that cause the motion. In the video, kinematics equations are used to describe and analyze the motion of an object in terms of its velocity, displacement, and time. These equations are essential for solving various problems related to the motion of objects, such as calculating the speed of a falling ball or the time it takes for an object to cover a certain distance.

💡Manipulating Formulas

Manipulating formulas refers to the process of rearranging mathematical equations to solve for different variables. This is a crucial skill in physics, as it allows for the calculation of unknown quantities based on known values. In the context of the video, the ability to manipulate kinematics equations enables the viewer to solve a variety of problems, such as finding the time it takes for an object to travel a certain distance given its velocity.

💡Velocity

Velocity is a physical quantity that describes the rate of change of an object's position with respect to time, having both magnitude and direction. In the video, velocity is one of the key variables in the kinematics equations, used to calculate the speed of an object and its change in position over time. The script explains how to rearrange the velocity equation to solve for different variables, such as distance or time.

💡Acceleration

Acceleration is the rate of change of velocity of an object with respect to time, and it indicates how quickly the velocity is changing. In the video, acceleration is discussed as a key concept in kinematics, with equations provided to calculate it based on changes in velocity and time. The script also demonstrates how to manipulate these equations to solve for other variables, such as time or distance.

💡Displacement

Displacement refers to the change in position of an object, and it is a vector quantity, meaning it has both magnitude and direction. In the video, displacement is used in the kinematics equations to describe the straight-line distance an object has moved from its initial position to its final position. The script shows how to rearrange the equations to solve for displacement when other variables are known.

💡Rearrangement of Equations

Rearrangement of equations is the process of changing the form of an equation to isolate a particular variable on one side of the equation. This is a fundamental skill in solving physics problems, as it allows for the calculation of unknowns based on known values. The video script provides examples of how to rearrange kinematics equations to solve for various variables, such as time, velocity, and acceleration.

💡Units of Measurement

Units of measurement are standardized quantities used to express the magnitude of physical quantities. In the context of the video, it is important to use consistent units, such as meters for distance, seconds for time, and meters per second for velocity, to ensure that the calculations are accurate and physically meaningful. The script emphasizes the importance of checking the units when rearranging and solving kinematics equations.

💡Distance

Distance is a scalar quantity that represents the total length of the path traveled by an object. In the video, distance is a key variable in the kinematics equations, and the script explains how to solve for distance using different arrangements of the velocity and acceleration equations. Understanding the concept of distance is crucial for analyzing the motion of objects in physics.

💡Time

Time is a fundamental physical quantity that measures the duration of events or the intervals between them. In the video, time is one of the variables in the kinematics equations, and the script demonstrates how to solve for time by rearranging the equations involving velocity, acceleration, and distance.

💡Initial Velocity

Initial velocity is the velocity of an object at the starting point of its motion. In the video, the concept of initial velocity is used in the kinematics equations to calculate other quantities such as final velocity, displacement, and acceleration. The script provides examples of how to solve for other variables when the initial velocity is known or assumed to be zero, as in the case of an object dropped from rest.

💡Final Velocity

Final velocity is the velocity of an object at the end point of its motion or at a specific time interval. The video script discusses how to calculate final velocity using the kinematics equations, often in relation to initial velocity, acceleration, and time. The ability to solve for final velocity is essential for understanding the changes in an object's motion over time.

Highlights

Manipulating kinematics equations is a key skill in understanding physics.

Rearrange equations to solve for different variables using the opposite operation.

The velocity formula (v = d/t) can be rearranged to solve for distance (d = vt) or time (t = d/v).

Acceleration is calculated by the change in velocity over time (a = (vf - vi) / t).

To solve for time in the acceleration equation, multiply both sides by t (t = (vf - vi) / a).

Solving for final velocity involves isolating vf (vf = (t * a) + vi).

Initial velocity can be found by rearranging the equation (vi = vf - (a * t)) and subtracting the acceleration component.

When solving distance formulas, aim to eliminate fractions by performing opposite operations.

The rearranged distance formula for time (t = 2d / (vf + vi)) is useful when dealing with objects starting from rest.

Average velocity is calculated by the total distance traveled divided by the total time taken (v_avg = d / t).

Units must be consistent when solving equations; for example, distance and velocity units should match.

When vi is zero, the distance formula simplifies to d = 0.5 * a * t^2, useful for problems involving free fall.

Solving for time when vi is zero involves taking the square root of the equation (t = sqrt(2d / a))

Acceleration can also be solved for by focusing on the differences in velocity and applying unit analysis (a = (vf^2 - vi^2) / 2d).

Unit analysis is a powerful tool to check the validity of the rearranged equations and their solutions.

The video provides practical examples of how to manipulate formulas to solve for various kinematic variables.

Understanding the relationships between distance, velocity, acceleration, and time is crucial in kinematics.

Transcripts

Browse More Related Video

High School Physics: Kinematic Equations

Creating And Using Kinematic Equations Chart - Kinematics - Physics

The Guess Method to Solve Every Physics Problem (Easy)

How to Remember/Derive the Kinematics Equations

Implicit Differentiation Day 1

Calculus 1: Separation of Variables Examples

Related Tags

Physics Education Kinematics Formulas Equation Manipulation Problem Solving Velocity Calculation Acceleration Concepts Distance and Time Learning Resource Video Tutorial Physics Principles