Creating And Using Kinematic Equations Chart - Kinematics - Physics

The Physics Universe
13 Sept 202306:14
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial teaches viewers how to create a kinematics equation chart to solve various kinematic problems efficiently. It introduces the five fundamental kinematic variables: displacement (Δx), initial velocity (v_i), final velocity (v_f), acceleration (a), and time (t). The video then presents four key kinematic equations and explains how to identify which equation to use based on the given and unknown variables in a problem. A practical example involving a car's acceleration and travel distance over time is used to demonstrate the application of the chart, guiding learners to quickly and accurately determine the displacement using the second kinematic equation.

Takeaways
  • 📚 Understand the five kinematic variables: displacement (Δx), initial velocity (v_i), final velocity (v_f), acceleration (a), and time (t).
  • 🧩 Create a kinematics equation chart to solve kinematic problems by identifying which equation to use based on given and unknown variables.
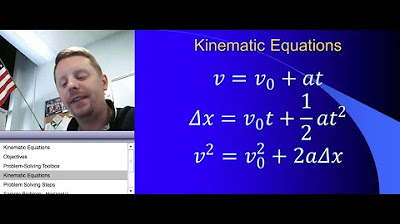
  • 🔍 The first kinematic equation is v_f = v_i + a*t, which helps find the final velocity when initial velocity, acceleration, and time are known.
  • 🔍 The second equation, Δx = v_i*t + 0.5*a*t^2, is used when you need to calculate displacement with initial velocity, acceleration, and time.
  • 🔍 The third equation, v_f^2 = v_i^2 + 2*a*Δx, relates final velocity, initial velocity, and displacement without involving time.
  • 🔍 The fourth equation, Δx = (v_i + v_f)/2 * t, is used when displacement, initial and final velocities, and time are given or needed.
  • 💡 Identify the unnecessary variable for a problem by its absence in the equation, which will guide you to the correct kinematic equation to use.
  • 🚗 Apply the kinematics chart to real-world problems, such as calculating the distance a car travels given its initial speed, acceleration, and time.
  • 📝 Always write down the given and unknown variables, and use the unmatched variable to find the appropriate equation on the chart.
  • 🔢 Substitute the known values into the chosen equation to solve for the unknown variable, following the principles of algebra.
  • 📈 The kinematics chart is a valuable tool for quickly selecting the correct equation and solving a wide range of motion problems.
Q & A

  • What is the main purpose of creating a kinematics equation chart?

    -The main purpose of creating a kinematics equation chart is to help determine which equation to use when solving a particular kinematic equation problem by identifying the given and unknown variables.

  • What are the five kinematic variables mentioned in the video?

    -The five kinematic variables are displacement (ΔX), initial velocity (VI), final velocity (VF), acceleration (a), and time (t).

  • What is the first kinematic equation presented in the video?

    -The first kinematic equation presented is VF = VI + at, which relates final velocity, initial velocity, acceleration, and time.

  • How can you identify which equation to use when solving a problem?

    -To identify which equation to use, you should list the given and unknown variables, and then look for the equation where the unnecessary variable is shaded in the kinematics chart.

  • What is the significance of shading a variable in the kinematics chart?

    -Shading a variable in the kinematics chart signifies that the variable is not needed to solve the problem, which helps in determining the appropriate equation to use.

  • What is the second kinematic equation and what variables does it involve?

    -The second kinematic equation is ΔX = v_i * t + (1/2)a*t^2, involving displacement, initial velocity, acceleration, and time, but not the final velocity.

  • In the example problem about the car, what are the given values and what is being asked?

    -In the example problem, the car has an initial speed (v_i) of 5 meters per second, accelerates (a) at 3 meters per second squared, and the time (t) is 5 seconds. The problem asks for the displacement (ΔX) the car travels during this time.

  • How is the displacement calculated in the example problem?

    -The displacement is calculated using the second kinematic equation (ΔX = v_i * t + (1/2)a*t^2) with the given values: initial velocity (5 m/s), acceleration (3 m/s^2), and time (5 s), resulting in a displacement of 62.5 meters.

  • What is the final kinematic equation presented in the video, and which variables does it include?

    -The final kinematic equation presented is ΔX = (1/2)(v_i + VF)*t, which includes displacement, initial velocity, final velocity, and time, but not acceleration.

  • How does the kinematics chart help in solving kinematic problems?

    -The kinematics chart helps by providing a visual representation of the relationships between the kinematic variables in different equations. It assists in quickly identifying the correct equation to use based on the given and unknown variables, streamlining the problem-solving process.

  • What is the importance of understanding the relationships between the kinematic variables?

    -Understanding the relationships between the kinematic variables is crucial for solving motion-related problems accurately and efficiently. It allows for the correct application of mathematical models to describe and predict the behavior of objects in motion.

Outlines
00:00
📚 Introduction to Kinematics Equation Chart

This paragraph introduces the concept of a kinematics equation chart, which is a tool to help solve kinematic problems. It explains the five kinematic variables: displacement (ΔX), initial velocity (VI), final velocity (VF), acceleration (a), and time (t). The paragraph then presents the four fundamental kinematic equations and emphasizes the importance of identifying which variable is not present in a given problem to select the appropriate equation for solving it. The process of elimination is introduced as a method to determine the correct equation to use based on the known and unknown variables.

05:00
🔍 Applying the Kinematics Chart to a Problem

In this paragraph, the speaker demonstrates how to apply the kinematics chart to a real-world problem. The example given involves a car accelerating from an initial speed of 5 m/s with an acceleration of 3 m/s² for a duration of 5 seconds. The goal is to find the displacement during this time. The paragraph explains how to identify the given and unknown variables, use the chart to find the correct equation (ΔX = v_i t + 1/2 a t²), and then substitute the known values into the equation to calculate the displacement. The final answer is 62.5 meters, illustrating the practical application of the kinematics chart in solving motion problems.

Mindmap
Keywords
💡Kinematics
Kinematics is the branch of physics that deals with the motion of objects without considering the forces that cause the motion. In the context of the video, it is the main theme, focusing on how to describe and predict the motion of an object based on its displacement, velocity, and acceleration over time. The video script discusses various kinematic equations and variables, highlighting their importance in solving motion-related problems.
💡Equation Chart
An equation chart is a visual representation that organizes and presents different equations in a structured way. In the video, the equation chart is a tool used to help viewers understand which kinematic equation to use based on the given variables in a problem. It is a helpful guide that simplifies the process of problem-solving by visually indicating which equation is relevant when certain variables are known or unknown.
💡Displacement (ΔX)
Displacement, denoted as ΔX, refers to the change in position of an object from its initial position to its final position. It is one of the five kinematic variables discussed in the video and is a key factor in calculating the motion of an object. The script mentions displacement multiple times, emphasizing its role in the kinematic equations and providing examples of how to calculate it based on other known variables.
💡Initial Velocity (VI)
Initial velocity, or VI, is the velocity of an object at the starting point of its motion. It is a critical kinematic variable that, along with other variables like acceleration and time, helps determine the object's behavior and final position. The video script explains how initial velocity is used in various kinematic equations to solve for different outcomes, such as final velocity or displacement.
💡Final Velocity (VF)
Final velocity, or VF, is the velocity of an object at the end of a specified time period or after it has undergone certain motion. The video script discusses final velocity in the context of kinematic equations, showing how it can be calculated if other variables like initial velocity, acceleration, and time are known. It is an essential aspect of understanding the overall motion analysis presented in the video.
💡Acceleration (a)
Acceleration, represented by 'a', is the rate of change of velocity of an object with respect to time. It is a central concept in kinematics and is crucial for determining how quickly an object's velocity changes during motion. The video script includes acceleration in several kinematic equations, demonstrating its impact on the object's final velocity, displacement, and overall motion轨迹.
💡Time (t)
Time, denoted as 't', is a fundamental variable in kinematics that represents the duration of an object's motion. It is used in conjunction with other kinematic variables to calculate various aspects of motion, such as displacement and final velocity. The video script emphasizes the importance of time in kinematic equations and provides examples of how it interacts with other variables to determine the outcome of the motion.
💡Kinematic Equations
Kinematic equations are mathematical formulas that relate the motion of an object to its displacement, velocity, acceleration, and time. The video script presents several of these equations, explaining how they can be used to solve for unknown variables in motion problems. These equations are the core of the video's educational content, teaching viewers how to apply them in different scenarios.
💡Problem Solving
Problem solving, as discussed in the video, involves applying kinematic equations to determine unknown variables in a motion scenario. The script provides a systematic approach to solving these problems, including the creation of a kinematics chart to aid in selecting the appropriate equation based on the given information. This process is essential for understanding and applying the principles of kinematics.
💡Variable Identification
Variable identification is the process of determining which variables are given and which are unknown in a problem. This is crucial in the context of the video, as it helps in selecting the correct kinematic equation to use for solving a particular problem. The script emphasizes the importance of identifying the 'not needed' variable, which is shaded in the equation chart, to guide the choice of the appropriate equation.
Highlights

Creating a kinematics equation chart is introduced as a helpful tool for solving kinematic problems.

Five kinematic variables are identified as displacement (ΔX), initial velocity (VI), final velocity (VF), acceleration (a), and time (t).

Four kinematic equations are presented, derived from previous videos, to relate the five variables.

The method of identifying the correct equation to use involves looking at the given and unknown variables and selecting the one with the unnecessary variable shaded in green.

An example problem is provided, involving a car with an initial speed of 5 m/s accelerating at 3 m/s^2 for 5 seconds, and the goal is to find the displacement.

The process of solving the example problem is demonstrated by writing down all variables, filling in known values, and using the kinematics chart to find the correct equation.

The second kinematic equation is used for the example, as the final velocity (VF) is the unnecessary variable, and the displacement (ΔX) is what is being sought.

The solution to the example problem is calculated by substituting known values into the selected kinematic equation, resulting in a displacement of 62.5 meters.

The video emphasizes the importance of understanding which variables are given and which are unknown to select the appropriate kinematic equation.

The kinematics chart is a visual aid that helps in quickly identifying the correct equation based on the provided and required information.

The video provides a clear and structured approach to solving kinematic problems, making it accessible for learners.

The practical application of the kinematics chart is demonstrated through a real-world scenario involving a car's motion.

The video content is designed to enhance problem-solving skills in kinematics and加深对物理定律的理解 (deepen the understanding of physical laws).

The use of the kinematics chart is promoted as an efficient method to tackle a variety of kinematic problems, showcasing its versatility.

The video concludes by reinforcing the steps to use the kinematics chart effectively, ensuring the viewer has a clear understanding of the process.

Transcripts

Browse More Related Video

Deriving Kinematic Equations (UPDATED) - Kinematics - Physics

High School Physics: Kinematic Equations

Deriving Kinematic Equations - Kinematics - Physics

AP Physics B Kinematics Presentation #03

How to Remember/Derive the Kinematics Equations

MCAT Physics Kinematic Equations and Knowing Which To Use

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Kinematics ChartMotion AnalysisPhysics TutorialEquation SolverEducational ContentLearn PhysicsMechanics PrinciplesMath for EngineersVideo LessonProblem Solving