How to solve for ACCELERATION (tagalog)

Teacher May
17 Mar 202109:12
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the concept of acceleration and its calculation using the formula a = (vf - vi) / t, where a is acceleration, vf is final velocity, vi is initial velocity, and t is time. It presents three problems involving different scenarios: a car slowing down, a bicycle coming to a stop, and an elevator accelerating upward. The script guides the viewer through the process of identifying given values and solving for the unknown, demonstrating how to apply the formula in various contexts.

Takeaways
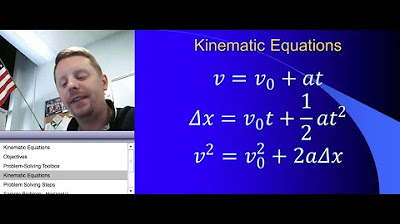
  • 📝 The basic formula for acceleration is a = (vf - vi) / t, where vf is final velocity, vi is initial velocity, and t is time.
  • 🔄 Using the magic triangle, one can derive the Manhattan and formula for time: t = (vf - vi) / a.
  • 🚗 In a problem-solving example, a car slows down from 35 m/s to 8 m/s in 7 seconds, and its acceleration is calculated as -3.86 m/s².
  • 🚴 Jesse's bicycle comes to a complete stop in 3 seconds with a deceleration of -5 m/s², starting from an initial velocity of 15 m/s.
  • 🏢 The elevators in the Landmark Tower in Yokohama accelerate at 3 m/s² for 4 seconds, reaching a final speed of 12 m/s starting from rest.
  • 📐 The script demonstrates the application of the basic kinematic equations in various real-world scenarios.
  • ⏱️ Time can be calculated using the formula t = (vf - vi) / a when the acceleration and initial and final velocities are known.
  • 📈 The concept of negative acceleration is introduced, representing deceleration or slowing down.
  • 🔢 The script emphasizes the importance of correctly applying the formulas for acceleration, velocity, and time in physics problems.
  • 🌟 The Landmark Tower elevators' speed highlights the practical use of kinematic equations in engineering and technology.
  • 📚 The script serves as an educational tool, teaching the application of fundamental physics concepts to solve for different variables in motion scenarios.
Q & A

  • What is the formula for acceleration given in the transcript?

    -The formula for acceleration is a = (vf - vi) / t, where vf is the final velocity, vi is the initial velocity, and t is the time.

  • How is the Manhattan formula derived from the basic acceleration formula?

    -The Manhattan formula for time, t = (vf - vi) / a, is derived by rearranging the basic acceleration formula to solve for time.

  • What is the formula for final velocity in terms of acceleration, initial velocity, and time?

    -The formula for final velocity is vf = a * t + vi, where a is the acceleration, t is the time, and vi is the initial velocity.

  • A car is traveling north at 35 meters per second and slows down to 8 meters per second in 7 seconds. What is its acceleration?

    -The car's acceleration is -3.86 meters per second squared. This is calculated using the formula a = (vf - vi) / t, where vf is 8 m/s, vi is 35 m/s, and t is 7 seconds.

  • How long would it take for Jesse to bring his bicycle to a complete stop from an initial velocity of 15 meters per second with an acceleration of -5 meters per second squared?

    -It would take Jesse 3 seconds to bring his bicycle to a complete stop. This is found using the formula t = (vf - vi) / a, where vf is 0 m/s (since it comes to a stop), vi is 15 m/s, and a is -5 m/s^2.

  • What is the final speed of the elevators in the Landmark Tower in Yokohama, Japan, if they accelerate upward at 3 meters per second squared for 4 seconds starting from rest?

    -The final speed of the elevators is 12 meters per second. This is calculated using the formula vf = a * t + vi, where a is 3 m/s^2, t is 4 seconds, and vi is 0 m/s (since it starts from rest).

  • What is the initial velocity of the car mentioned in the transcript?

    -The initial velocity of the car mentioned in the transcript is 35 meters per second.

  • What is the final velocity of the car after it slows down?

    -After slowing down, the car's final velocity is 8 meters per second.

  • How long does the car take to slow down from 35 m/s to 8 m/s?

    -The car takes 7 seconds to slow down from 35 m/s to 8 m/s.

  • What is the acceleration of the elevators in the Landmark Tower?

    -The acceleration of the elevators in the Landmark Tower is 3 meters per second squared.

  • How long do the elevators in the Landmark Tower accelerate for?

    -The elevators in the Landmark Tower accelerate for 4 seconds.

  • What is the initial speed of Jesse's bicycle?

    -The initial speed of Jesse's bicycle is 15 meters per second.

  • What is the final speed of Jesse's bicycle when it comes to a complete stop?

    -The final speed of Jesse's bicycle when it comes to a complete stop is 0 meters per second.

Outlines
00:00
📐 Velocity and Acceleration Calculations

This paragraph introduces the basic principles of velocity and acceleration calculations using the formula vf - vi / t, where vf stands for final velocity, vi for initial velocity, and t for time. It explains how to derive equations for acceleration (a = (vf - vi) / t) and time (t = (vf - vi) / a), and also presents the final velocity formula (vf = a * t + vi). The paragraph then applies these formulas to a real-world scenario of a car slowing down from 35 m/s to 8 m/s in 7 seconds, demonstrating how to find the car's acceleration, which is calculated to be -3.86 m/s^2.

05:04
🚴 Bicycle Deceleration and Elevator Speed

The second paragraph discusses two additional problems related to velocity and acceleration. The first problem involves calculating the time it takes for a bicycle to come to a complete stop with a given initial velocity and deceleration rate. The second problem is about determining the final speed of elevators in the Landmark Tower, Yokohama, which accelerate at a rate of 3 m/s^2 for 4 seconds from rest. The paragraph provides a step-by-step approach to solving these problems, emphasizing the application of the velocity and acceleration formulas in different contexts.

Mindmap
Keywords
💡Acceleration
Acceleration is a physical quantity that describes the rate of change of velocity of an object. It is typically measured in meters per second squared (m/s^2). In the context of the video, acceleration is used to calculate how quickly a car slows down, a bicycle comes to a stop, or an elevator reaches its final speed. The formula for acceleration is given as 'a = (vf - vi) / t', where 'a' is acceleration, 'vf' is final velocity, 'vi' is initial velocity, and 't' is time.
💡Velocity
Velocity refers to the speed of an object in a specific direction. It is a vector quantity, meaning it has both magnitude (speed) and direction. In the video, both initial and final velocities are crucial in determining the acceleration and time involved in various motion scenarios. The term is used to describe the motion of a car, a bicycle, and an elevator.
💡Time
Time is the continuous, irreversible flow of events from the past, through the present, to the future. In the context of the video, time is a key variable in the equations that describe motion. It is used to calculate how long it takes for an object to change its velocity due to acceleration or deceleration.
💡Formula
A formula is a mathematical statement that expresses a relationship between quantities. In the video, several formulas are used to relate velocity, acceleration, and time in different motion scenarios. These formulas are essential tools for problem-solving and understanding the dynamics of moving objects.
💡Deceleration
Deceleration is the rate at which an object's velocity decreases over time. It is a type of acceleration but with a negative value since it is in the opposite direction of the motion. Deceleration is used in the video to describe the slowing down of objects such as a car or a bicycle.
💡Final Velocity
Final velocity is the speed of an object at the end of a certain time period or after a specific event. It is an essential component in the equations that describe the motion of objects, particularly in relation to acceleration and initial velocity. In the video, final velocity is used to calculate the stopping point of a bicycle and the speed of an elevator.
💡Initial Velocity
Initial velocity is the speed of an object at the beginning of a motion event or time period. It is a critical starting point for calculating changes in velocity and understanding the dynamics of motion. The video uses initial velocity in conjunction with acceleration and time to solve for various outcomes.
💡Magic Triangle
The term 'magic triangle' in the video is a metaphorical reference to the set of equations that relate velocity, acceleration, and time. These equations form a 'triangle' of relationships that can be used to solve for any one of the three variables when the other two are known.
💡Problem Solving
Problem solving involves a systematic approach to finding solutions to given problems. In the context of the video, problem solving is demonstrated through the application of physical formulas to determine unknown quantities such as acceleration, time, or final velocity based on provided data.
💡Elevator
An elevator is a type of vertical transportation that moves people or goods between floors (levels, decks) of a building, vessel, or other structure. The video discusses the acceleration of elevators in the Landmark Tower in Yokohama, Japan, as an example of applying motion formulas to real-world technology.
💡Motion
Motion refers to the process of change in the position of an object. It is a fundamental concept in physics and is central to the video's discussion of how objects move and change speed under the influence of forces such as acceleration and deceleration.
Highlights

Derivation of acceleration formula from the basic kinematic equation.

Use of a magic triangle to derive multiple kinematic equations.

Explanation of the Manhattan formula for time in relation to velocity and acceleration.

Derivation of the final velocity formula from the basic kinematic equation.

Problem-solving example of a car slowing down with given initial velocity, final velocity, and time.

Calculation of the car's acceleration with a step-by-step approach.

Application of the acceleration formula to find the time taken to stop a bicycle from a given initial velocity.

Solution for the time taken with a clear explanation of the formula and substitution of given values.

Real-world application of the kinematic equations with the example of the fastest elevators in the Landmark Tower, Yokohama, Japan.

Explanation of how to find the final speed of an object given constant acceleration and time, starting from rest.

Step-by-step calculation of the final speed of the elevators, showcasing the practical use of the kinematic equations.

In-depth analysis of the kinematic equations and their practical applications in solving motion-related problems.

Comprehensive coverage of the basic kinematic equations and their derivations, providing a solid foundation for understanding motion.

The use of negative values in the acceleration formula to represent deceleration.

Clear and detailed explanation of how to handle and solve for negative values in kinematic equations.

Transcripts

Browse More Related Video

Solving Three Acceleration Problems

High School Physics: Kinematic Equations

How to Calculate Velocity

Creating And Using Kinematic Equations Chart - Kinematics - Physics

MELC-Based Science 7 Lesson || Describing Motion || Acceleration

Projectile Motion Time of Flight Formula Derivation

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ConceptsMotion AnalysisAcceleration CalculationVelocity FormulasReal-world ApplicationsCar DecelerationBicycle BrakingElevator SpeedMathematical Problem SolvingKinematicsMechanics