Multivariable Calculus Lecture 1 - Oxford Mathematics 1st Year Student Lecture
TLDRThe transcript discusses the concept of double integrals, extending from single-variable calculus to multiple dimensions, focusing on 3D space. It explains the informal definition of a double integral, its properties, and provides examples of integrating over rectangular and more complex domains. The importance of choosing the right order of integration and utilizing properties like linearity, order, and domain splitting for simpler computations is emphasized. The session ends with a teaser for the next lecture on changing coordinate systems for easier integration of complex domains.
Takeaways
- 📚 The course builds upon introductory calculus, extending its concepts to multiple dimensions, particularly 3D space.
- 📈 The informal definition of a line integral is revisiting, focusing on the area under a curve as the integral's value.
- 🔍 The concept of partitioning an interval into subintervals is introduced, which helps in computing integrals through limits.
- 📊 Double integrals are introduced as a generalization of single-variable integrals, focusing on integrating functions over a 2D region.
- 🔧 The process of double integration involves partitioning the plane into small elements and summing their volumes under a surface.
- 📐 The properties of double integrals such as linearity, order, and domain splitting are discussed, aiding in their computation.
- 📈 An example of integrating over a rectangular domain is provided, illustrating the process and the choice between integrating with respect to X or Y first.
- 🌟 The importance of choosing the order of integration based on the problem's nature is emphasized, as it can simplify the process.
- 📊 A more complex example involving a parabolic region is discussed, highlighting the need to carefully consider limits and the order of integration.
- 🔄 The concept of changing coordinate systems, such as from Cartesian to polar coordinates, is mentioned as a tool for simplifying complex integrals.
- 🔜 The next lecture will focus on integrating over more complex domains and the benefits of using different coordinate systems for these tasks.
Q & A
What is the main focus of the course described in the transcript?
-The main focus of the course is to extend the concepts learned in introductory calculus into multiple dimensions, specifically working in 3D. This involves exploring integrals in 3D, differentiating in 3D, and developing theorems to write down physical laws using the approaches derived in the course.
How is the informal definition of a line integral in one dimension described in the transcript?
-The informal definition of a line integral in one dimension is described as the area under a curve on a closed interval. It involves subdividing the interval into subintervals and approximating the integral with rectangles whose height is the function value at a point within the subinterval. The integral is then the limit of the sum of these rectangles as the size of the subintervals tends to zero.
What is the significance of the function f(x) in the context of the line integral?
-In the context of the line integral, the function f(x) represents a real-valued function that takes values on the interval AB. The integral of f(x) with respect to x between certain limits involves finding the area under the curve of this function over the specified interval.
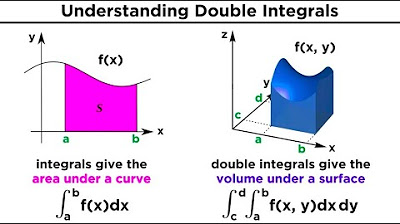
How does the concept of a double integral in two dimensions relate to that of a single integral in one dimension?
-The concept of a double integral in two dimensions extends the idea of a single integral in one dimension by considering the integral over a two-dimensional region. Instead of finding the area under a curve, a double integral computes the volume under a surface defined by a scalar field (function) over a region in the plane.
What is the purpose of partitioning the plane into small elements in the context of a double integral?
-Partitioning the plane into small elements is done to approximate the double integral. The process involves summing the volumes under the surface over these small elements and then taking the limit as the size of the elements tends to zero, which gives the exact value of the double integral.
What are the key properties of double integrals mentioned in the transcript?
-The key properties of double integrals mentioned in the transcript include linearity, order, and domain splitting. Linearity allows for the integral of a linear combination of functions to be expressed as the sum of the integrals of the individual functions. The order property states that if one function is always greater than or equal to another on a region, then the integral of the first function will be greater than or equal to the integral of the second. Domain splitting allows for the integral over a region to be split into integrals over subregions that make up the original region.
How does the order of integration affect the computation of a double integral?
-The order of integration can affect the ease and simplicity of computing a double integral. In some cases, integrating first with respect to one variable and then the other can lead to a simpler calculation, especially when dealing with complex domains. However, for continuous and bounded functions on a rectangular domain, the order of integration does not affect the final result.
What is the significance of the property of domain splitting in double integrals?
-The property of domain splitting is significant because it allows for the simplification of the integration process. If a region can be split into subregions, the double integral over the entire region can be expressed as the sum of the double integrals over the subregions. This can make the computation more manageable, especially for complex regions.
How does the transcript illustrate the computation of a double integral over a rectangular domain?
-The transcript illustrates the computation of a double integral over a rectangular domain by considering the integral of the function x^2*y^3 over the region bounded by x from 1 to 2 and y from 1 to 3. It shows that the order of integration (whether integrating with respect to x first or y first) does not affect the final result, which in this case is 140/3.
What is the example given in the transcript for calculating the area of a region bounded by certain curves?
-The example given in the transcript for calculating the area of a region is the area bounded by the parabola y = sqrt(x), the x-axis, and the line y = x - 2. The computation involves integrating with respect to x first and then y, requiring careful consideration of the limits of integration based on the geometry of the region.
What is the final result of the area computation for the region bounded by the parabola y = sqrt(x), the x-axis, and the line y = x - 2?
-The final result of the area computation for the region bounded by the parabola y = sqrt(x), the x-axis, and the line y = x - 2 is 10/3.
Outlines
📚 Introduction to Advanced Calculus
The paragraph introduces the course as a natural progression from introductory calculus, mentioning overlapping material for familiarity with concepts. The focus is on extending ideas from 2D to 3D, including integrals and differentiation in three dimensions, and developing theorems for physical laws.
📐 Fundamentals of Line Integrals
This section delves into the informal definition of line integrals, emphasizing the concept of integrating a function over a closed interval. It explains the process of partitioning the interval into subintervals and approximating the integral with rectangles, leading to the formal definition involving limits.
📐 Extending to Double Integrals
The paragraph discusses the transition from one-dimensional integrals to two-dimensional double integrals. It introduces the concept of integrating a scalar field over a region in the plane, using the analogy of computing the volume under a surface. The process of partitioning the plane into small elements and summing their volumes is described.
📐 Properties of Double Integrals
This section outlines important properties of double integrals, including linearity, order of integration, and domain splitting. It emphasizes that these properties can simplify the computation of integrals and provides a brief overview of how they can be exploited in practical scenarios.
📐 Integrating Over Rectangular Domains
The paragraph focuses on the straightforward computation of double integrals over rectangular domains. It explains that the order of integration does not affect the result and provides an example of integrating a function over a simple square region, highlighting the ease of computation due to the domain's simplicity.
📐 Choosing the Order of Integration
This section discusses the strategic choice of the order of integration based on the nature of the problem. It contrasts the process of integrating first with respect to X and then Y versus the reverse, using an example to illustrate how the choice can affect the complexity of calculations.
📐 Integrating Over Non-Rectangular Domains
The paragraph addresses the more complex task of integrating over non-rectangular domains, using the example of calculating the area of a region bounded by a parabola, the x-axis, and a line. It emphasizes the importance of carefully determining the limits of integration and the potential need to split the domain for easier computation.
📚 Summary and Preview of Future Topics
In conclusion, the paragraph recaps the discussion on integrating over simple and complex domains, highlighting the importance of choosing an appropriate order of integration. It also provides a preview of upcoming topics, which will include more complex domains and the use of different coordinate systems to simplify integration.
Mindmap
Keywords
💡Calculus
💡Multiple Dimensions
💡Integrals
💡Differentiation
💡Scalar Field
💡Double Integrals
💡Linearity
💡Order of Integration
💡Domain Splitting
💡Volume Integrals
💡Physical Laws
Highlights
The course builds upon introductory calculus, extending its concepts to multiple dimensions and 3D space.
There is some overlapping material with introductory calculus to help familiarize students with the notation and methods used in the course.
The focus is on developing theorems that allow the writing of physical laws using the approaches derived from calculus.
The informal definition of a line integral is discussed, relating to the area under a curve on a graph.
Subdividing the interval AB into subintervals helps in computing the area under the curve for a line integral.
The integral of a function is shown to exist provided that the function is continuous.
Double integrals are introduced as an extension of single integrals, dealing with two-dimensional regions.
Double integrals compute the volume under a surface in a 3D space.
The process of partitioning the plane into small elements and summing their volumes is outlined for computing double integrals.
Properties of double integrals, such as linearity, order, and domain splitting, are discussed to simplify their computation.
An example of integrating a function over a rectangular domain is provided, illustrating the process of double integration.
The order of integration can affect the simplicity of the computation, and it is sometimes advantageous to integrate over one variable first.
The concept of domain splitting is used to simplify the computation of double integrals over certain regions.
The importance of drawing diagrams to visualize the domain and limits of integration is emphasized.
An example of calculating the area of a region bounded by a parabola, the x-axis, and a line is given, demonstrating the application of double integrals.
The computation involves careful determination of the limits of integration, especially for more complex domains.
The transcript concludes with a mention of future lectures on integrating over more complex domains and the use of different coordinate systems.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: