Lec 16: Double integrals | MIT 18.02 Multivariable Calculus, Fall 2007
TLDRThis script from an MIT OpenCourseWare lecture introduces the concept of double integrals, transitioning from single-variable integrals to their two-variable counterparts. It explains how double integrals measure the volume under a surface defined by a function of two variables. The lecture delves into the definition, computation, and practical application of double integrals, including setting up bounds for integration and the use of iterated integrals. It also touches on the importance of the order of integration and the conditions under which the order can be switched, providing examples to illustrate the process.
Takeaways
- 📚 The lecture introduces the concept of double integrals as an extension of single-variable integrals, emphasizing the transition from finding areas to calculating volumes under surfaces defined by functions of two variables.
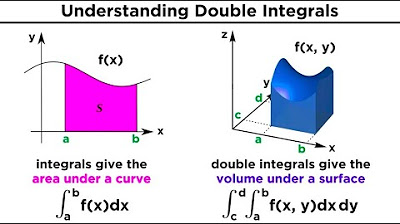
- 📉 The script explains that the double integral of a function over a region corresponds to the volume under the graph of the function, similar to how a single integral corresponds to the area under a curve.
- 📏 The importance of the region of integration in the xy-plane (R) is highlighted, as the double integral measures the volume of the solid above this region.
- 📐 The process of defining a double integral involves dividing the region into infinitesimally small pieces (delta A) and summing the product of the function's value and the area of each piece, taking the limit as the size of the pieces approaches zero.
- 🔍 The script illustrates the concept of iterated integrals, where the double integral is computed by first integrating over one variable with the other held constant, and then integrating the result over the second variable.
- 📝 The computation of double integrals typically involves setting up the integral with appropriate bounds for both variables and then solving the inner integral before the outer integral.
- 🔄 The order of integration can be switched in double integrals, but this requires careful reconsideration of the bounds for each variable, as they may depend on the other variable.
- 📈 An example is provided to demonstrate the computation of a double integral in a simple case where the region of integration is a rectangle, making the bounds constant and straightforward.
- 🤔 The challenges of integrating certain functions, like e^y/y, are discussed, and the utility of switching the order of integration to make the problem more tractable is highlighted.
- 📊 The script concludes with a discussion on the potential to use polar coordinates for double integrals, which may simplify calculations in cases where the region or the function has a more complex geometry or symmetry.
Q & A
What is the main topic discussed in the video script?
-The main topic discussed in the video script is double integrals, including their definition, motivation, and the process of calculating them.
What is the basic idea behind a double integral?
-The basic idea behind a double integral is to find the volume under a surface defined by a function of two variables over a certain region in the xy-plane.
How does the concept of a double integral relate to the integral of a function of one variable?
-The concept of a double integral relates to the integral of a function of one variable in that both are used to find areas or volumes. While a single integral finds the area under a curve between two points, a double integral finds the volume under a surface over a region.
What is the meaning of 'dA' in the context of double integrals?
-In the context of double integrals, 'dA' stands for a small piece of area within the region of integration in the xy-plane.
How are double integrals typically defined rigorously?
-Double integrals are typically defined rigorously by dividing the region of integration into small pieces (such as rectangles), finding the volume of the small box under the graph for each piece, and then taking the limit as the size of these pieces goes to zero.
What is an iterated integral and why is it used in double integrals?
-An iterated integral is a process where you perform one integral and then integrate the result with respect to another variable. It is used in double integrals to simplify the calculation by breaking it down into two single integrals, often making it easier to compute.
Why is it important to consider the order of integration when setting up double integrals?
-The order of integration is important because it affects the bounds of integration. The bounds for the inner integral depend on the outer variable, and vice versa. Choosing the correct order can simplify the calculation and make the problem more tractable.
What is the significance of the region's shape in the context of double integrals?
-The shape of the region is significant because it determines the bounds of integration. Some shapes may make it easier to integrate in one order rather than the other, and certain shapes may require different techniques, such as polar coordinates, for easier integration.
Can the order of integration be switched without any consequences?
-No, the order of integration cannot be switched without considering the new bounds for the integrals. The bounds must be adjusted according to the new order to ensure the correct volume or area is calculated.
How does the script illustrate the process of computing a double integral?
-The script illustrates the process of computing a double integral by first setting up the integral with the correct bounds, then computing the inner integral while holding the outer variable constant, and finally integrating the result of the inner integral with respect to the outer variable.
What is the purpose of providing examples in the script?
-The purpose of providing examples in the script is to demonstrate the application of the concepts discussed, to clarify how to set up and compute double integrals in different scenarios, and to highlight the importance of choosing the right order of integration.
How does the script suggest improving the calculation of a particular double integral involving e^y/y?
-The script suggests that instead of directly integrating e^y/y with respect to y, one should switch the order of integration, which simplifies the inner integral, and then complete the calculation using standard integration techniques.
What mathematical technique is hinted at for solving integrals that seem difficult with the given function?
-The script hints at using integration by parts or trigonometric substitution as mathematical techniques for solving difficult integrals, such as those involving e^y/y.
What alternative method for calculating double integrals is mentioned in the script for the next session?
-The script mentions that polar coordinates will be introduced as an alternative method for calculating double integrals, which can be easier for certain types of regions and functions.
Outlines
📚 Introduction to Double Integrals
The paragraph introduces the concept of double integrals as a natural progression from single-variable integrals to functions of two variables. It explains the motivation behind double integrals by relating them to the calculation of areas under a curve for single-variable functions and extends this to the calculation of volumes under surfaces for two-variable functions. The double integral is presented as a way to measure the volume under the graph of a function z = f(x, y) over a specified region in the xy-plane. The notation dA for a small area element is introduced, and the double integral is symbolized with two integral signs, indicating the integration over a region R.
📐 Defining Double Integrals Rigorously
This section delves into a more rigorous definition of double integrals by drawing an analogy to the Riemann sum approach used in single-variable calculus. The process involves dividing the region under consideration into small pieces, calculating the volume of a small box for each piece, and then summing these volumes to estimate the total volume. The double integral is defined as the limit of this process as the size of the pieces approaches zero. The paragraph also discusses the importance of choosing the right method for calculating double integrals, hinting at the reduction of a double integral to two single integrals, and the relevance of single-variable calculus techniques.
📉 Computing Double Integrals Through Iteration
The paragraph explains the process of computing double integrals by reducing them to iterated integrals, which involve integrating with respect to one variable while treating the other as a constant. It describes the method of slicing the region by parallel planes and integrating over these slices to find the volume. The concept of an iterated integral is introduced, where the inner integral is performed first, followed by the outer integral. The importance of understanding the bounds of integration and how they may vary depending on the variable being integrated is emphasized.
🔍 Example of a Double Integral Over a Rectangle
This paragraph presents a practical example of calculating a double integral over a rectangular region. The function to be integrated is 1 - x^2 - y^2, and the region is defined by x between 0 and 1 and y between 0 and 1. The process involves setting up the iterated integral, computing the inner integral first with respect to y and then the outer integral with respect to x. The bounds for y are constant, simplifying the integration process. The final computation yields a volume of one third.
📈 Double Integrals and Region Bounds
The paragraph discusses the importance of correctly identifying the bounds of integration for double integrals, especially when the region is not a simple rectangle. It explains how the bounds for the inner integral depend on the outer variable, using the example of integrating over a quarter disk defined by x^2 + y^2 = 1 for x between 0 and 1. The bounds for y are derived from the equation of the circle, showing that the range of y values changes with x.
🧩 Integrating Over a Quarter Disk
This section provides a detailed example of integrating the same function, 1 - x^2 - y^2, but over a different region, specifically a quarter disk. The bounds for y are now dependent on x, with the upper limit given by the square root of (1 - x^2). The paragraph guides through the process of setting up the iterated integral, with the inner integral being with respect to y and the outer integral with respect to x, both ranging from 0 to 1.
🔄 Switching the Order of Integration
The paragraph explores the concept of switching the order of integration for double integrals, emphasizing the need to carefully reconsider the bounds of integration when doing so. It contrasts simple cases where the region is a rectangle and the order can be switched without issue, with more complex cases requiring a deeper analysis of the region's geometry. The importance of understanding how the slices of the region align with the variables of integration is highlighted.
📚 Example of Switching Orders for a Complex Region
This paragraph presents a complex example where the order of integration is switched for an integral involving the function e^y/y with bounds y from x to sqrt(x) and x from 0 to 1. The process involves visualizing the region and determining the new bounds for x when integrating with respect to y first, and then y when integrating with respect to x first. The example demonstrates the complexity of changing the order of integration and the need for a clear understanding of the region's geometry.
📉 Computing the Switched Integral
The paragraph details the computation of the switched integral from the previous example. It shows how to perform the inner integral with respect to x and then the outer integral with respect to y. The computation involves recognizing the function as an exponential function and using integration techniques to find the antiderivative. The final result is obtained by evaluating the antiderivative at the bounds of integration.
🌐 Upcoming Topic: Double Integrals in Polar Coordinates
The final paragraph previews the next topic to be covered: double integrals in polar coordinates. It suggests that the method of integrating in polar coordinates will provide an easier approach to certain types of double integrals, such as those involving circular or radial symmetry, which were difficult to handle with the current methods. The paragraph also hints at the applications of double integrals that will be explored in future lessons.
Mindmap
Keywords
💡Derivatives
💡Integrals
💡Double Integrals
💡Function of One Variable
💡Function of Two Variables
💡Volume
💡Iterated Integral
💡Region of Integration
💡Bounds of Integration
💡Polar Coordinates
💡Trigonometric Substitution
Highlights
Introduction to double integrals as an extension of single-variable integrals to calculate volumes under surfaces.
Explanation of the double integral as the limit of summing volumes of infinitesimally small boxes under the graph of a function.
Visual representation of double integrals through the integration over a region in the xy-plane.
Motivation for double integrals using the volume under the graph of a function of two variables.
Transition from understanding derivatives to focusing on integrals, specifically double integrals.
Illustration of the double integral process through a step-by-step breakdown of cutting and summing small areas.
Definition of the double integral in terms of summing the product of function values and small areas.
Introduction of the notation dA for an infinitesimally small area in the context of double integrals.
Explanation of the process of computing double integrals by reducing them to two single integrals.
Importance of understanding single-variable calculus for effectively computing double integrals.
Technique of using parallel planes to scan through a region for double integral computation.
Description of the iterated integral process where integration is performed first over y and then over x.
Clarification on the dependency of the bounds of integration on the outer variable in iterated integrals.
Example of computing the volume under a paraboloid using double integrals over a square region.
Demonstration of the setup for double integrals with easy bounds due to the rectangular region.
Step-by-step computation of a double integral including the inner and outer integrals.
Conversion of the area element dA into differentials dy dx based on the order of integration.
Discussion on the possibility of changing the order of integration and its implications on the bounds.
Computation of a double integral with a function that requires changing the order of integration for simplification.
Introduction to the concept of integrating in polar coordinates as a method for simplifying double integrals.
Anticipation of exploring applications of double integrals and their use in practical scenarios in future lessons.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: