Center of Mass & Centroid Problems - Calculus
TLDRThe video script discusses the concept of center of mass and moments in relation to a calculus course. It uses the example of a seesaw to explain moments as mass times distance from the axis of rotation and demonstrates how to balance a seesaw by placing the fulcrum at the center of mass. The script further explains how to calculate the center of mass for point masses in one and two dimensions, and for continuous mass distributions using integral calculus. The examples provided include finding the center of mass for various point mass systems and regions bounded by functions, emphasizing the importance of understanding moments and center of mass for problem-solving in physics and engineering.
Takeaways
- 📚 The concept of the center of mass is fundamental in understanding the balance of objects, especially in relation to rotation and forces acting on them.
- 🌟 The moment of an object is calculated as the product of its mass and the distance from the axis of rotation, and is a key factor in determining the balance of a system.
- ⚖️ To balance a seesaw, for example, the fulcrum must be placed at the center of mass, where the combined moments of all masses are equal.
- 📐 The center of mass for a system of point masses can be found using the formula: (sum of the product of each mass and its distance from the reference point) divided by the total mass.
- 🔍 For two-dimensional systems, both the x and y coordinates of the center of mass must be calculated, using moments about the respective axes and the total mass.
- 📈 In cases where the mass is distributed over an area, such as a surface, the concept of surface density is used, which is mass per unit area.
- 🤔 The center of mass of a continuous mass distribution can be determined by setting up and solving definite integrals related to the area and moments of the region.
- 📊 Practice problems are essential for applying the formulas and concepts learned, and for reinforcing the understanding of how to find the center of mass for various types of mass distributions.
- 🔄 The process of finding the center of mass involves both analytical calculations and geometrical intuition, particularly when visualizing the effects of moving masses and fulcrums.
- 🎓 A solid grasp of calculus, particularly integration, is crucial for advanced applications of center of mass calculations, especially in complex or irregular mass distributions.
- 🌐 The principles of center of mass are widely applicable in physics and engineering, impacting the stability and design of structures, machinery, and various other systems.
Q & A
What is the concept of a moment in the context of finding the center of mass?
-The moment is the product of mass and the distance from the axis of rotation. It represents the effectiveness of a force in causing a rotational effect around a specified point, known as the fulcrum.
How does the seesaw example illustrate the concept of moments?
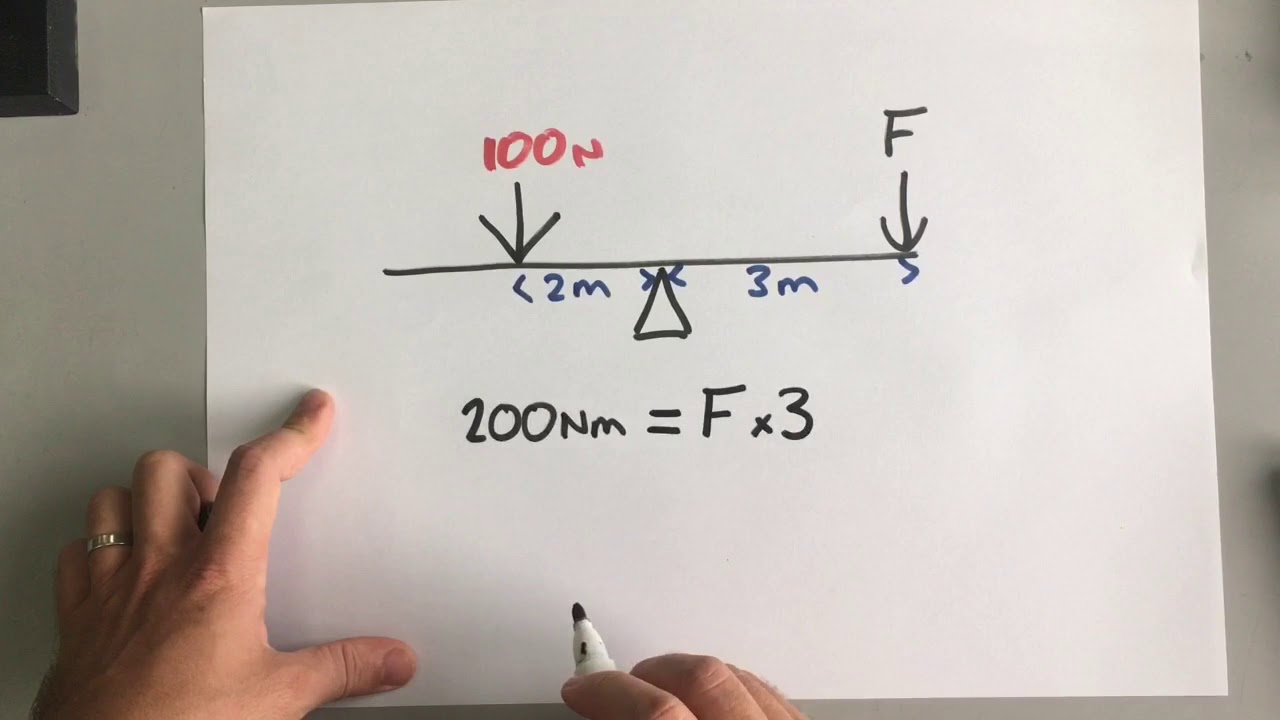
-In the seesaw example, the moments of the two masses (8 kg and 10 kg) are calculated based on their distances from the fulcrum. The 8 kg mass creates a moment of 32 kg*m (8 times 4 meters), while the 10 kg mass creates a moment of 50 kg*m (10 times 5 meters). The seesaw tips in the direction of the greater moment, which in this case is the left side with the 10 kg mass.
What is the formula to find the center of mass of a system?
-The center of mass (COM) of a system can be found by calculating the first moment (moment about the origin) and dividing it by the total mass of the system. For a one-dimensional system, the x-coordinate of the COM is given by the formula: (Σ(mi * xi) / Σmi), where mi is the mass of each object and xi is its distance from the reference point.
How can you balance a seesaw with two masses if you cannot move the blocks?
-You can balance the seesaw by positioning the fulcrum at the center of mass of the system. This point is where the sum of the moments (masses multiplied by their distances from the fulcrum) is zero when divided by the total mass of the system.
What is the significance of the center of mass in a two-dimensional system?
-In a two-dimensional system, the center of mass is the point at which the mass of the system can be considered to be concentrated. It's the balance point where the system would tilt or rotate if it were to be supported at that point. Calculating the center of mass is crucial in many applications, including engineering, physics, and computer graphics for simulating the behavior of objects.
How do you find the y-coordinate of the center of mass in a two-dimensional system?
-The y-coordinate of the center of mass in a two-dimensional system is found by calculating the moment about the x-axis and dividing it by the total mass. The formula is: (Σ(mi * yi) / Σmi), where mi is the mass of each object and yi is its vertical distance from the reference axis.
What is the role of density in finding the center of mass of a distributed mass?
-Density plays a crucial role in determining the mass of a region when dealing with distributed mass, such as a two-dimensional area. The mass of the region is calculated by multiplying the surface density (mass per unit area) by the area of the region. This mass is then used to calculate the center of mass.
How do you calculate the area under a curve?
-The area under a curve is calculated using definite integration. You find the difference between the integrals of the upper and lower functions (if any) over the specified interval. The area is given by the formula: ∫(from a to b) (upper function - lower function) dx, where 'a' and 'b' are the limits of integration.
What is the formula for finding the x-coordinate of the center of mass for a region bounded by two curves?
-The x-coordinate of the center of mass for a region bounded by two curves is given by the formula: (1/A) * ∫(from a to b) (x * (f(x) - g(x))) dx, where 'A' is the area under the curves, 'f(x)' is the upper curve function, and 'g(x)' is the lower curve function.
What is the process for finding the centroid of a region bounded by specific functions?
-To find the centroid of a region bounded by specific functions, first, determine the points of intersection of the functions, which define the limits of integration. Calculate the area under the curves using definite integration. Then, use the formulas for the x and y coordinates of the center of mass to find the centroid. These formulas involve integrating the product of the distance variable (x or y) and the difference of the functions, divided by the area, over the interval defined by the points of intersection.
What are the steps to find the y-coordinate of the center of mass for a distributed mass in a two-dimensional region?
-To find the y-coordinate of the center of mass for a distributed mass in a two-dimensional region, first calculate the area of the region using definite integration. Then, compute the moment about the x-axis by integrating half the product of the distance variable (x or y), the square of the upper function, and the difference of the functions over the interval. Finally, divide this moment by the total mass (area times surface density) to find the y-coordinate of the center of mass.
Outlines
📚 Introduction to Center of Mass and Moments
This paragraph introduces the concept of center of mass in relation to a calculus course, emphasizing the importance of understanding moments. A moment is defined as the product of mass and its distance from the axis of rotation. The example of a seesaw with masses on either side is used to illustrate how moments can determine the balance of an object. The seesaw example also introduces the concept of finding the fulcrum's position to balance the seesaw, which is related to finding the center of mass of the system.
🔍 Balancing the Seesaw: Center of Mass Calculation
The paragraph delves into the process of balancing the seesaw by placing the fulcrum at the center of mass. It explains how to calculate the center of mass along the x-axis using the moments of the masses and the total mass. The example continues with a practical demonstration of moving the fulcrum to achieve balance, and it reinforces the concept with a new scenario involving masses at different positions, leading to the calculation of the center of mass as x = -1.
📐 Finding the Center of Mass for Multiple Objects
This section extends the concept of center of mass to systems with multiple objects. It explains how to find the center of mass along the x-axis by dividing the total moment about the origin by the total mass of the system. The example provided involves point masses at various positions on the x-axis, and it guides through the calculation process, highlighting the distribution of mass and its effect on the center of mass location.
🤔 Moments and Center of Mass in Multi-Dimensional Systems
The paragraph discusses the concept of moments and center of mass in two-dimensional systems. It explains how to calculate the moment of a particle about the x-axis and y-axis, and how these relate to the center of mass coordinates. The explanation includes the formula for finding the y-coordinate of the center of mass in a two-dimensional system, and it provides a step-by-step approach to solving problems involving point masses in a plane.
📝 Calculating Center of Mass for Distributed Mass
This part of the script addresses the challenge of finding the center of mass for a mass distributed over an area, such as a surface with uniform density. It introduces the concepts of density, linear density, and surface density, and explains how these relate to the mass of a region. The paragraph outlines the process of calculating the center of mass coordinates by integrating over the area and using the surface density and area of the region.
🌟 Deriving Center of Mass Formulas for Two-Dimensional Regions
The paragraph focuses on deriving the formulas for the x and y coordinates of the center of mass for a two-dimensional region. It explains the process of calculating moments about the x and y axes and how these moments are related to the center of mass coordinates. The explanation includes the use of definite integrals and the relationship between mass, area, and density in the calculation process.
📊 Example Problem: Center of Mass for a Shaded Region
This section presents an example problem to find the center of mass for a shaded region bounded by two curves. It guides through the process of graphing the region, finding the points of intersection, calculating the area, and using the derived formulas to determine the center of mass coordinates. The example involves a square root function and a linear function, and it demonstrates the step-by-step calculation process.
🔢 Solving for Centroid in a Bounded Region
The paragraph continues with another example problem, focusing on identifying the centroid of a region bounded by specific functions. It explains the process of graphing the functions, finding the intersection points, calculating the area of the region, and determining the x and y coordinates of the centroid using the integral formulas. The example involves a parabola and a linear function, showcasing the application of the concepts discussed.
📈 Complex Example: Center of Mass for a Combined Region
The final paragraph presents a more complex example of finding the center of mass for a combined region defined by two functions. It details the steps of setting up the integrals, combining like terms, and evaluating the anti-derivatives to find the area and the center of mass coordinates. The example involves a parabola shifted upwards and a linear function, demonstrating the application of the derived formulas in a more intricate scenario.
Mindmap
Keywords
💡Center of Mass
💡Moment
💡Fulcrum
💡Seesaw
💡Integration
💡Density
💡Definite Integral
💡Anti-Derivative
💡Linear Density
💡Surface Density
Highlights
The video introduces the concept of center of mass and its relevance in a calculus course.
Understanding the concept of a moment, which is mass times the distance from the axis of rotation, is fundamental.
Using the seesaw example to illustrate moments and how they affect balance.
The moment of an object is calculated as mass times distance from the fulcrum.
The seesaw example demonstrates how the greater moment on one side causes imbalance and rotation.
Balancing the seesaw involves placing the fulcrum at the center of mass of the system.
The center of mass location is found by taking the moment about the origin and dividing by the total mass.
The video explains how to calculate the center of mass for multiple objects on the x-axis.
The center of mass can be found using the formula for moments and total mass for systems in one dimension.
The concept of moment is extended to two-dimensional systems, with the inclusion of the y-coordinate in the center of mass calculation.
The video provides a method to find the center of mass for a system of point masses in two dimensions.
For a mass distributed over an area, the center of mass can be found using surface density and definite integrals.
The formula for the x-coordinate of the center of mass involves the definite integral of the product of the density function and x, divided by the total area.
Similarly, the y-coordinate of the center of mass is found by integrating the product of the density function squared, divided by the total area.
The video demonstrates how to find the centroid of a region bounded by two functions using calculus.
The process of finding the area of a region bounded by curves is explained using definite integrals.
The video provides a step-by-step approach to find the center of mass for a two-dimensional region with variable density.
The concept of linear density and surface density is introduced, relating to one-dimensional and two-dimensional objects respectively.
The video concludes with practice problems to reinforce the understanding of finding the center of mass for various types of systems.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: