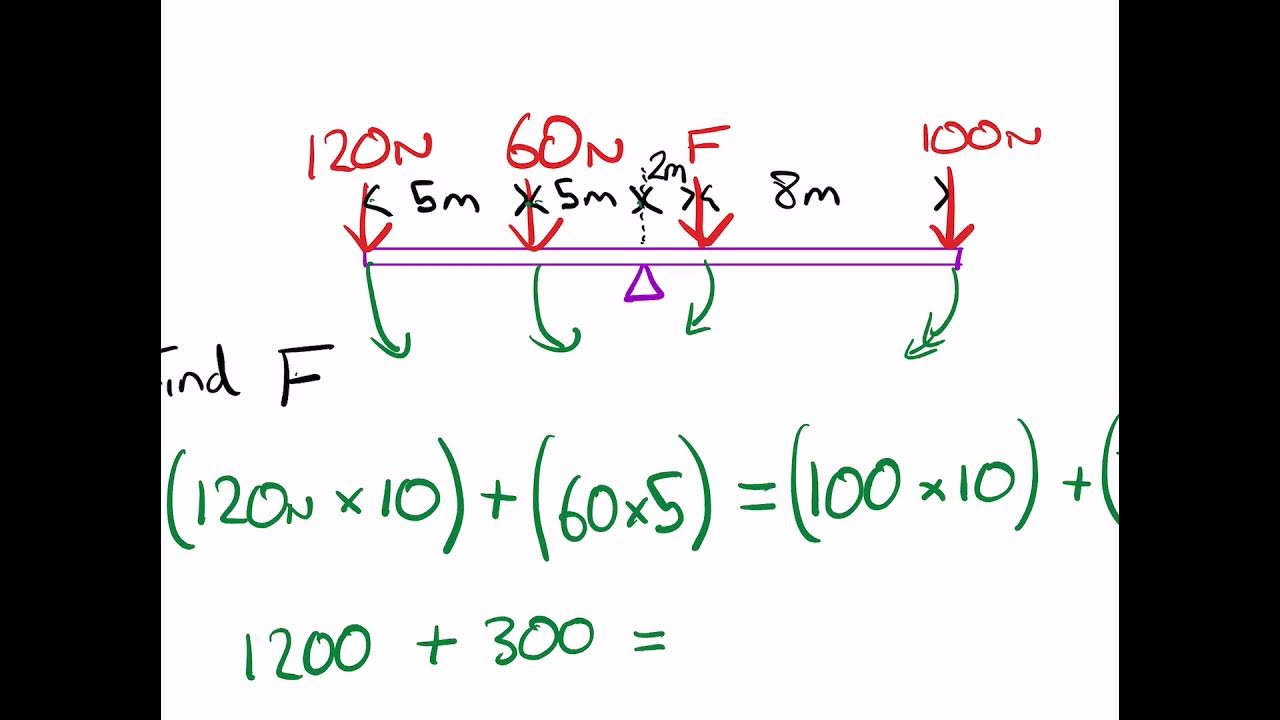GCSE Physics - Forces 5 - Moments and Centre of Mass
TLDRThis GCSE physics video explores the concept of moments, or turning forces, which act around a pivot point. It explains how moments are calculated as force times the perpendicular distance from the pivot, using door handles and seesaws as examples. The video also discusses balancing moments, circular motion, and the importance of center of mass in tipping objects over, such as a coffee box or a double-decker bus. It concludes with a practical demonstration on finding the center of mass for irregularly shaped objects.
Takeaways
- 🔧 Moments are turning forces that involve a pivot point where the object does not move.
- 🚪 Door handles are placed far from the hinges to maximize the moment, making it easier to open the door with less force.
- ⚖️ Moments are calculated by multiplying the force by the perpendicular distance from the pivot.
- 🤸♂️ In a seesaw, forces acting at different distances from the pivot create turning forces that can balance each other.
- 🔄 If moments are balanced, the object is in equilibrium and does not turn.
- 🏗️ Center of mass is crucial in understanding how objects balance and tip over.
- 🚌 High center of mass, like in a double-decker bus, increases the risk of tipping over.
- 📏 To find the center of mass of an irregular object, use the plumb line method by hanging the object from different points and drawing vertical lines.
- 📐 The intersection of the vertical lines from the plumb line method indicates the center of mass.
- 🔍 Understanding moments and center of mass helps explain everyday phenomena like door handles, seesaws, and bus safety.
Q & A
What is a moment in physics?
-A moment is a turning force that always involves a pivot. It is calculated as the force times the distance from the pivot.
Why are door handles placed far away from the hinges?
-Door handles are placed far from the hinges to create a larger turning force (moment) with a smaller force, making it easier to open the door.
What is a pivot in the context of moments?
-A pivot is a point on which an object does not move, serving as the central point around which the turning force acts.
How is the moment of a force calculated?
-The moment is calculated as the product of the force and the perpendicular distance from the pivot.
What happens when moments balance each other?
-When moments balance each other, the object is in equilibrium, meaning there is no net turning force and the object remains stationary.
How can you balance moments on a seesaw?
-To balance moments on a seesaw, the product of the force and distance from the pivot on one side must equal the product of the force and distance from the pivot on the other side.
What is the significance of the center of mass in relation to moments?
-The center of mass is the point where the mass of an object is concentrated. Its position relative to the pivot affects whether the object will tip over or remain stable.
How does the position of the center of mass affect the stability of a double-decker bus?
-If the center of mass is high, such as when many people are on the top deck, the bus is more likely to tip over. A lower center of mass makes the bus more stable.
How can you find the center of mass of an irregularly shaped object?
-To find the center of mass of an irregular object, hang the object from different points and draw vertical lines from the hanging points. The center of mass is where these lines intersect.
What is the difference between speed and velocity in the context of circular motion?
-Speed is a scalar quantity without direction, while velocity is a vector that includes direction. In circular motion, an object can have a constant speed but its velocity changes due to the changing direction, causing acceleration.
Outlines
🚪 Understanding Moments and Pivots
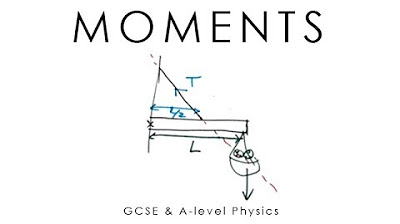
This paragraph introduces the concept of moments in physics, specifically within the context of a door's operation. It explains that moments are turning forces that require a pivot, which is a stationary point. The door hinge serves as the pivot, and the door handle's distance from this pivot is crucial because it determines the amount of force needed to open the door. The further the handle, the less force is required due to the increased moment, calculated as force times the perpendicular distance from the pivot. The paragraph also touches on balancing moments, using the seesaw as an example to illustrate how forces of different magnitudes can balance each other out when their distances from the pivot are appropriately adjusted.
🔄 Circular Motion and the Center of Mass
This section delves into the relationship between moments, circular motion, and the concept of vectors and scalars. It clarifies that while speed is a scalar quantity, velocity is a vector and thus has direction, which changes as an object moves in a circle. This change in direction means the object is constantly accelerating, even if its speed remains constant. The paragraph further explains how moments can cause objects to tip over, using a coffee box as an example, and introduces the center of mass as a critical factor in determining an object's stability. The center of mass is the point where an object's mass is concentrated, and its position relative to the pivot affects whether the object will tip over when a moment is applied.
🧩 Finding the Center of Mass in Irregular Shapes
The final paragraph discusses the importance of the center of mass in understanding how moments affect the stability of objects, especially those with irregular shapes. It demonstrates how to find the center of mass of an oddly shaped piece of foam by suspending it from different points and drawing vertical lines from where the string hangs. The intersection of these lines indicates the center of mass. This method is a practical approach to determining the balance point of objects with complex geometries, which is essential for understanding how they will respond to applied moments.
Mindmap
Keywords
💡Moment
💡Pivot
💡Force
💡Distance
💡Equilibrium
💡Center of Mass
💡Velocity
💡Acceleration
💡Scalar
💡Vector
Highlights
Moments are a turning force involving a pivot, which is a fixed point that doesn't move.
Door handles are placed far from hinges to maximize the turning force with less effort.
A moment is calculated as the force multiplied by the perpendicular distance from the pivot.
In a seesaw, the pivot remains stationary while forces cause a turning motion.
Moments can balance each other out if the clockwise and anti-clockwise moments are equal.
Unbalanced moments cause an object to keep turning around the pivot.
Circular motion involves constant changes in velocity direction, resulting in acceleration.
An object's center of mass is the point where its entire mass is considered to be concentrated.
For an object to tip over, the center of mass must be outside its base of support.
The center of mass affects the stability of objects, like how double-decker buses need a low center of gravity to avoid tipping.
To find the center of mass of irregular shapes, use a pin and string method to determine the point where vertical lines intersect.
A moment that is not balanced results in the object experiencing rotational motion.
The difference between speed and velocity: speed is scalar (magnitude only), while velocity is a vector (magnitude and direction).
Acceleration occurs even if an object moves at a constant speed in a circular path because the direction of velocity changes.
When dealing with moments, ensure that the force is perpendicular to the pivot to correctly calculate the turning force.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: