Center of Mass | Physics with Professor Matt Anderson | M12-04
TLDRThe video script delves into the concept of the center of mass, explaining its importance and how to calculate it for both discrete and continuous objects. It begins with a simple square object to illustrate the calculation method, where the center of mass is found to be at the geometric center. The script then transitions to a more complex object, like a rock, and describes a practical method for determining its center of mass by balancing it on different edges and finding the intersection of the vertical lines drawn from these points of balance. This technique is not only a scientific exercise but also an art form, as seen in rock balancing at the San Diego harbor. The video emphasizes the role of the center of mass in maintaining balance and the skill required to achieve it with irregular objects.
Takeaways
- 🧮 The concept of the center of mass is crucial for understanding how objects balance and is defined as the point where the total mass of the object is concentrated.
- 📐 For simple shapes like a square with equal masses at each corner, the center of mass is at the geometric center, which is also the center of the square.
- 🔍 To calculate the center of mass for discrete particles, you sum the product of each particle's mass and its position, then divide by the total mass.
- 📊 For objects with a continuous mass distribution, like a 'blob', the summation becomes an integral, and you integrate the product of mass elements and their positions over the entire object.
- 🤔 Determining the center of mass of an irregular object, such as a rock, can be done by balancing it on different points and finding the intersection of the vertical lines drawn from the points of balance.
- ⚖️ The point of balance on an object is directly beneath its center of mass, which is a key principle used in balancing rocks or other objects.
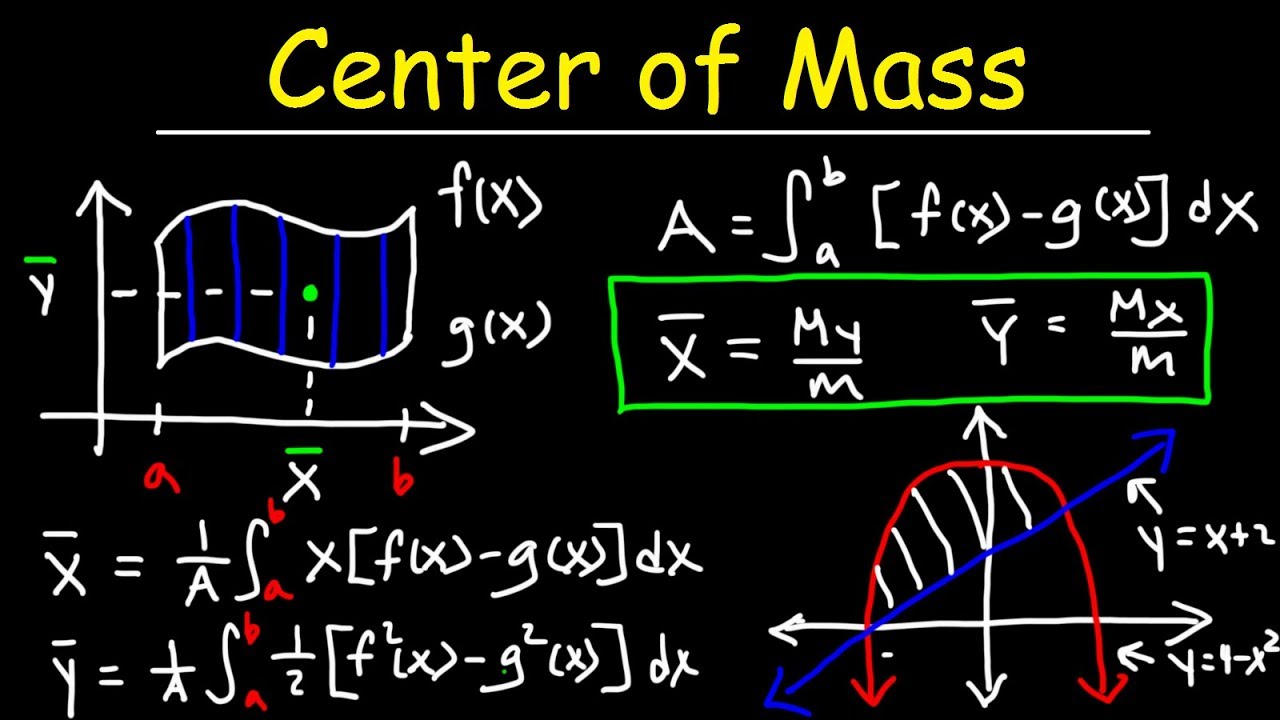
- 📍 The x and y coordinates of the center of mass can be found by setting up equations based on the mass distribution and solving for the position where the sums of moments cancel out.
- 🤹♂️ Balancing complex objects requires adjusting the object until the center of mass is directly above the point of contact, which can be a challenging task.
- 🏋️♂️ In practice, finding the center of mass can involve physical manipulation, like tilting the object until it stands on an edge, and then finding the intersection of the vertical lines from the points of balance.
- 🌌 The process of balancing rocks is an artistic expression as well as a demonstration of the principles of physics.
- ⚙️ Understanding the center of mass is not only important in physics but also has practical applications in various fields, including engineering and art.
- 🎭 The ability to balance objects like rocks is a skill that requires a keen understanding of the center of mass and a lot of practice.
Q & A
What is the concept of the center of mass?
-The center of mass is the point at which the mass of an object can be considered to be concentrated. For a uniform object, it is the geometric center.
How do you determine the center of mass for a simple object like a square with equal masses at each corner?
-For a symmetrical object like a square with equal masses at each corner, the center of mass is at the geometric center of the square.
What is the formula for calculating the x-position of the center of mass for discrete particles?
-The x-position of the center of mass is calculated as the sum of the product of each particle's mass (m_i) and its x-position (x_i), divided by the total mass of the system.
How does the formula for the center of mass change when dealing with a continuous distribution of matter?
-For a continuous distribution, the summation becomes an integral, and the mass (m) becomes an infinitesimally small mass element (dm). The formula then involves integrating the product of the position (x or y or z) and the mass element over the entire object and dividing by the total mass.
What is a practical method to find the center of mass of an irregularly shaped object like a rock?
-A practical method involves placing the object on a surface and finding a point where it can balance. By rotating the object and finding another edge on which it can balance, the intersection of the lines drawn vertically through these points of balance indicates the center of mass.
Why is the center of mass important when balancing objects on top of each other?
-The center of mass must be directly above the contact point between the objects for them to balance. If the center of mass is not aligned above the contact point, the object will tilt and eventually fall due to the torque created by gravity.
What happens if an object is tilted slightly off its center of mass?
-If an object is tilted slightly off its center of mass, the force of gravity acting on the center of mass will create a torque that causes the object to fall in the direction of the tilt.
How does the symmetry of an object affect its center of mass?
-The symmetry of an object greatly affects its center of mass. For symmetrical objects, the center of mass will be at the geometric center. For asymmetrical objects, the center of mass will be at the point where the weighted distribution of mass is balanced.
What is the significance of the center of mass in the context of physics?
-The center of mass is significant in physics as it is the point about which an object can be rotated without causing a change in its motion. It is also the point that governs how an object will respond to external forces and is critical in the study of mechanics and dynamics.
Can the center of mass be outside the physical material of an object?
-Yes, the center of mass can be outside the physical material of an object. This is often the case in objects with uneven mass distribution, such as a ring or a hollow sphere, where the center of mass is in the empty space in the middle.
How does the distribution of mass within an object affect its center of mass?
-The distribution of mass within an object directly affects its center of mass. If the mass is distributed evenly, the center of mass will be at the geometric center. If the mass is concentrated in certain areas, the center of mass will shift towards those areas.
What role does the center of mass play in the stability of structures?
-The center of mass plays a crucial role in the stability of structures. For a structure to be stable, its center of mass must be within its base of support. If the center of mass is outside the base of support, the structure will be unstable and may collapse.
Outlines
🧮 Understanding the Center of Mass
The paragraph begins with an explanation of the concept of the center of mass. It emphasizes the importance of accurately defining the center of mass and provides a method to calculate its position. Using a hypothetical square object with equal masses at each corner, the speaker demonstrates how to determine the center of mass by drawing a coordinate system and applying the formula for the x and y positions. The formula involves summing the product of each mass and its respective coordinate, then dividing by the total mass. The example concludes with a confirmation that the center of mass for a symmetrical object like a square is indeed at its geometric center.
📏 Calculating the Center of Mass for Discrete and Continuous Objects
This paragraph delves into how to find the center of mass for both discrete particles and continuous distributions of matter. It explains that for discrete particles, the center of mass can be found using a summation, while for continuous objects, an integral must be used. The speaker illustrates the transition from summation to integration in the formula. The paragraph also discusses a practical method for finding the center of mass of an irregular object, such as a rock, by balancing it on a table and drawing lines from the points of contact until they intersect at the center of mass. This technique is used by rock balancers at the harbor, who adjust the rock until the center of mass is directly above the contact point for a stable balance.
🎭 The Art and Physics of Balancing
The final paragraph discusses the skill and artistry involved in balancing objects, especially when the base of support is small compared to the size of the object. It highlights the challenge of achieving the precise balance point, which is directly beneath the center of mass. The speaker explains the physics behind the balancing act: any tilt to the side results in a torque that causes the object to fall in that direction due to gravity acting on the center of mass. The paragraph concludes by acknowledging the difficulty of this task and expressing admiration for those skilled in the art of balancing, viewing it as a remarkable combination of art and physics.
Mindmap
Keywords
💡Center of Mass
💡Coordinate System
💡Mass
💡Integral
💡Discrete Particles
💡Continuous Distribution
💡Balance Point
💡Symmetry
💡Torque
💡Balancing Rocks
💡Blob
Highlights
The concept of the center of mass is introduced and its importance in defining the balance point of an object is emphasized.
A method to calculate the center of mass for a simple object, like a square with equal masses on each side, is explained.
The formula for calculating the x and y position of the center of mass is provided, using summation notation.
An example calculation confirms the center of mass of a symmetrical square object is at its geometric center.
The process of finding the center of mass for a more complex, non-symmetrical object, like a rock, is discussed.
A practical technique for determining the center of mass of an irregular object by balancing and drawing intersection lines is demonstrated.
The significance of the center of mass in the art of rock balancing is highlighted, showing how it must be directly above the contact point for stability.
The concept of torque and how it affects the balance of an object is explained in the context of the center of mass.
The transition from calculating the center of mass for discrete particles to a continuous distribution is discussed.
The integral form of the center of mass calculation for a continuous distribution is introduced.
The challenge of finding the center of mass in three dimensions is acknowledged.
An interactive approach to finding the center of mass by physically manipulating the object is suggested.
The role of the center of mass in ensuring stability when balancing objects, such as in rock balancing at the harbor, is explained.
The skill required to balance objects based on the center of mass is recognized as a combination of art and physics.
The difficulty of achieving precise balance with a large and complex object on a small contact point is discussed.
The importance of the center of mass in practical applications, such as stacking rocks, is demonstrated through real-world examples.
The process of finding the center of mass through trial and error by adjusting the object until it achieves balance is described.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: