Motion of the Center of Mass
TLDRIn this informative video, Mr. Andersen explores the concept of center of mass and its crucial role in understanding the motion of objects. Using the example of Weebles, he explains how the low center of mass allows them to wobble without falling. He further illustrates the importance of identifying an object's center of mass to accurately describe its linear motion, as demonstrated with a hammer throw and a rotating object. The video also introduces a practical hang test for determining the center of mass in irregular objects, emphasizing its application in physics problems.
Takeaways
- 🎯 The concept of center of mass is crucial for understanding the motion of objects.
- 🤹 Weebles demonstrate the principle of center of mass through their egg-shaped design with a low center, allowing them to wobble but not fall.
- 🏋️ Objects with a low center of mass are more stable and resist falling over when pushed.
- 🔄 When an object is out of equilibrium, its center of mass may temporarily shift but will return to its original position.
- 🌀 Weebles' looping action when thrown or spun in the air illustrates the object revolving around its center of mass.
- 📏 The center of mass is the average position of an object's mass, often located within the object.
- 🛠 To measure linear motion, one must identify the displacement of the center of mass over time.
- 🏹 The center of mass of a hammer is towards the top due to its heavy head, affecting its trajectory when thrown.
- 🚲 In physics problems, identifying the center of mass of complex objects like bicycles simplifies the analysis by ignoring internal forces.
- 📐 The hang test is a practical method to determine the center of mass for irregularly shaped objects.
- 🔄 Both linear and rotational motion can be analyzed by considering the movement of the center of mass.
Q & A
What is the main topic of the video?
-The main topic of the video is the concept and application of the center of mass in understanding the motion of objects.
What toy serves as a real-life example to explain the concept of center of mass?
-Weebles serve as a real-life example to explain the concept of center of mass.
Why do Weebles wobble but not fall down when pushed?
-Weebles wobble but do not fall down because their center of mass is located very low due to the dense bottom part of their egg-shaped design.
How does the center of mass affect the motion of an object when it is thrown or spun in the air?
-When an object is thrown or spun in the air, it revolves around its center of mass, which allows it to perform a looping action.
What is the significance of the center of mass in measuring linear motion?
-The center of mass is significant in measuring linear motion because it allows us to accurately describe the motion of an object by determining its displacement and subsequently its velocity and acceleration.
How does the center of mass of a hammer behave when thrown?
-When a hammer is thrown, its center of mass, which is closer to the top due to the heavy head, moves in a straight line, while the hammer itself may appear to move in a random motion.
What is the importance of knowing the center of mass when solving physics problems?
-Knowing the center of mass is important in physics problems because it simplifies the analysis by allowing us to ignore internal forces and focus only on the external forces acting on the object.
How can you determine the center of mass of an object with uniform density?
-For an object with uniform density, the center of mass will be at the geometric center, such as the middle of a sphere, cube, or cylinder.
What is the hang test and how is it used to find the center of mass of an irregular object?
-The hang test involves hanging the object from different points and drawing a vertical line from each point. The intersection of these lines is the center of mass of the object.
How is the velocity of an object calculated when it is rotating around its center of mass?
-The velocity of an object rotating around its center of mass is calculated by dividing the distance traveled by the center of mass (displacement) by the time taken, just as it is done for linear motion.
What is the role of the center of mass in analyzing forces on an object?
-The center of mass helps in analyzing the forces on an object by allowing us to consider the object as a single entity, where internal forces balance each other out, and only external forces are considered in the analysis.
Outlines
🤔 Understanding the Center of Mass with Weebles
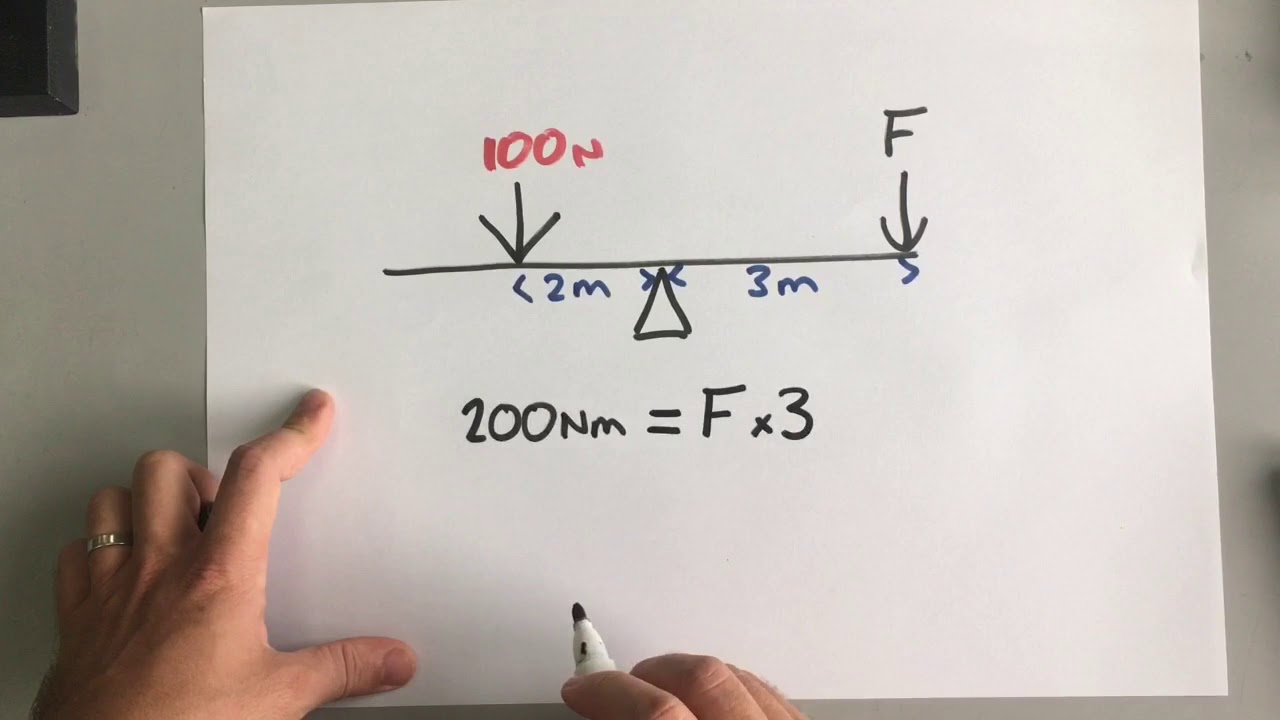
This paragraph introduces the concept of the center of mass using the example of Weebles, a popular toy known for their ability to wobble without falling over. The explanation focuses on the egg-shaped design of Weebles with a dense bottom that keeps the center of mass low, allowing the toy to return to its original position when pushed. The importance of understanding the center of mass for analyzing linear motion and displacement is highlighted, as well as its relevance in calculating velocity and acceleration. The paragraph also touches on the application of this concept in understanding the motion of objects like hammers and bicycles, emphasizing the simplification of internal forces when the center of mass is known.
Mindmap
Keywords
💡Center of Mass
💡Wobble
💡Equilibrium
💡Displacement
💡Velocity
💡Acceleration
💡Internal Forces
💡External Forces
💡Hang Test
💡Rotation
Highlights
The physics principle behind Weebles' ability to wobble but not fall is explained, which is related to the concept of center of mass.
Weebles are egg-shaped with a dense bottom, resulting in a very low center of mass that prevents them from falling over when pushed.
When a Weeble is pushed, its center of mass momentarily raises but then wobbles back to its original position, demonstrating the concept of equilibrium.
Weebles can perform a looping action when thrown or spun in the air due to their center of mass acting as the axis of rotation.
The center of mass is crucial for accurately describing the motion of an object, as it is the mean position of the matter's distribution.
Displacement can be determined by finding the center of mass at the beginning and end of an object's motion.
Velocity is calculated by dividing displacement by time, which can be applied to understand the motion of an object's center of mass.
Acceleration is found by examining changes in velocity over time, which is essential for analyzing an object's motion.
The motion of a thrown hammer or an ax is influenced by their center of mass, which is typically closer to the heavier end.
By focusing on the center of mass, internal forces within an object can be ignored, simplifying the analysis of its motion under external forces.
The center of mass of a bicycle is located towards the middle, which is important for solving physics problems treating the bicycle as a single object.
For uniform density objects, the center of mass is located at the geometric center, such as in a sphere, cube, or cylinder.
The center of mass of two spheres would be located exactly in the middle between them.
For irregular objects, the center of mass can be determined using a hang test, where the object is suspended and balanced points are marked and intersected.
Measuring linear motion involves determining the initial and final positions of the center of mass and calculating velocity and acceleration accordingly.
When an object rotates, its velocity can still be determined using the same principles of displacement and time, even though the motion is rotational.
The video emphasizes the practical application of understanding and using the center of mass to measure and analyze the linear and rotational motion of objects.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: