Logarithms - e - Euler's Number
TLDRThe video script delves into the concept of 'e', a fundamental number in mathematics, revealing its value and diverse applications. 'e', approximately equal to 2.718281828, emerges from various mathematical contexts such as compound interest, logarithms, and series summation. The script explains how 'e' can be calculated using limits and factorials, highlighting its unique properties, including the fact that the derivative and antiderivative of e^x are the same, and its graph represents both a curve and the area under it. The explanation is engaging, offering a comprehensive understanding of 'e' and its significance.
Takeaways
- 📌 The mathematical constant 'e' is approximately equal to 2.718281828 and is found in various areas of mathematics.
- 🧮 'e' can be derived from the compound interest formula, where it represents the limit as the number of compounding periods (n) approaches infinity.
- 💰 When the interest rate is 100% and the compounding is continuous (n approaches infinity), the future value of an investment is 'e' times the principal.
- 📈 The value of 'e' can also be calculated as the limit of (1 + 1/n)^(1/n) as n approaches zero.
- 🔢 Another method to find 'e' is by summing the series from n equals zero to infinity of 1/n! (factorial).
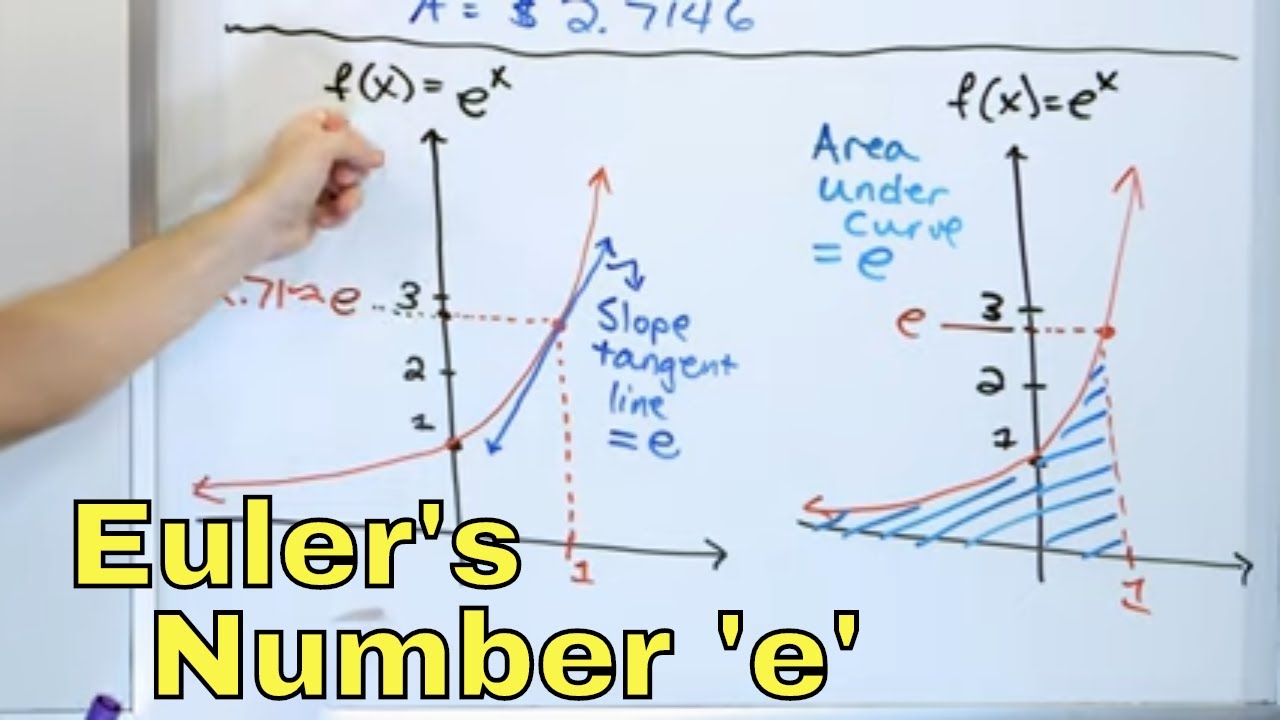
- 🏢 The function y = e^x has a unique property where its derivative is also e^x, meaning the slope of the tangent line at any point equals the y-value.
- 🌐 The area under the curve y = e^x from negative infinity to any value x is equal to the y-value at that x, representing the total growth of the function up to that point.
- 📚 The number 'e' is also known as Euler's number and has wide applications in calculus and other mathematical fields.
- 🔍 To approximate 'e', one can use large values for n in the compound interest formula or incrementally sum the 1/n! series.
- 📊 The graph of y = e^x is a straight line with a slope equal to 1, starting from the point (0, 1).
- 🌟 Understanding 'e' and its properties is crucial for studying exponential growth, decay, and related mathematical models.
Q & A
What is the mathematical constant 'e'?
-The mathematical constant 'e' is approximately equal to 2.718281828, and it is a fundamental number in mathematics, appearing in various equations and formulas, including those related to exponential growth and decay.
How is the number 'e' used in logarithms?
-The number 'e' is the base for natural logarithms, denoted as 'ln'. For example, ln(5) represents the natural logarithm of 5, which is the same as log base 'e' of 5.
What is the compound interest formula, and how does it relate to 'e'?
-The compound interest formula is a = P(1 + r/n)^(n*t), where 'a' is the future amount, 'P' is the principal investment, 'r' is the interest rate, 'n' is the number of times interest is paid per year, and 't' is the number of years. As 'n' approaches infinity, the formula yields 'e', demonstrating one way to calculate the value of 'e'.
How does the limit of (1 + 1/n)^n as n approaches infinity give the value of 'e'?
-As 'n' becomes very large, the expression (1 + 1/n)^n converges to the value of 'e'. This is a mathematical demonstration of how continuous compounding leads to the discovery of 'e'.
What is another formula that can be used to calculate the value of 'e'?
-Another formula to calculate 'e' is the limit as n approaches 0 of (1 + n)^(1/n). This formula also converges to 'e' as 'n' gets closer to zero.
How does the sum of 1/n! from n equals 0 to infinity represent the value of 'e'?
-The sum of 1/n! (n factorial) from n equals 0 to infinity also converges to 'e'. This series representation is a less common but equally valid way to calculate 'e'.
What is the significance of the graph y = e^x, and how does it relate to the derivative?
-The graph y = e^x is a straight line with a slope equal to the y value at any point. This is significant because the derivative of e^x with respect to x is also e^x, meaning the slope of the tangent line at any point on the curve is equal to the height of the curve at that point.
How is the area under the curve y = e^x related to the function itself?
-The area under the curve y = e^x from negative infinity to any value 'x' is equal to the value of the function at 'x'. This is because the antiderivative of e^x is e^x, and evaluating this antiderivative from negative infinity to 'x' gives the area under the curve.
What are some applications of the number 'e' in mathematics?
-The number 'e' has numerous applications in mathematics, including exponential growth and decay problems, compound interest calculations, natural logarithms, and in calculus, where it is the base for the natural exponential function and is used in finding derivatives and integrals.
How can one approximate the value of 'e' using a calculator?
-One can approximate the value of 'e' by plugging in a very large number for 'n' in the expression (1 + 1/n)^n or by calculating the sum of 1/n! for increasing values of 'n'. Most calculators have a built-in 'e' function that can directly provide the value of 'e' to a specified precision.
What is Euler's number, and how is it related to the mathematical constant 'e'?
-Euler's number is another name for the mathematical constant 'e'. It is named after the Swiss mathematician Leonhard Euler, who made significant contributions to the understanding and application of 'e' in various mathematical fields.
Outlines
📈 Understanding the Mathematical Constant e and its Origin
This paragraph introduces the mathematical constant e, explaining its prevalence in various mathematical functions such as exponentials and logarithms. It delves into the historical context of e and describes its approximate value. The paragraph then transitions into a discussion about the compound interest formula, using it to illustrate how the value of e can be derived when the number of compounding periods (n) approaches infinity. The explanation includes a practical example of an investment and how the future value changes with different compounding frequencies, ultimately highlighting that the limit of (1 + 1/n)^n as n approaches infinity equals e.
🧮 Deriving the Value of e through Different Mathematical Expressions
This section builds upon the previous explanation by presenting alternative methods to calculate the value of e. It introduces another expression, the limit of (1 + n)^(1/n) as n approaches zero, which also equals e. The paragraph provides a detailed table of values to demonstrate how this expression converges to e as n becomes very small. Additionally, it introduces a series expansion method, the sum of 1/n! from n=0 to infinity, to approximate e. The explanation includes the calculation of individual factorials and their reciprocals, culminating in a sum that approximates the value of e closely. This part of the script emphasizes the versatility of e in mathematical calculations and its unique properties.
📊 Applications and Properties of e: The Graph and Its Derivative
The final paragraph shifts focus to the practical applications and properties of e, particularly highlighting its role as Euler's number. It describes the graph of y=e^x and notes that the derivative of this function is also e^x, indicating that the slope of the tangent line at any point on the curve is equal to the y-value at that point. The paragraph further discusses the concept of area under the curve, explaining that the area from negative infinity to a point x can be calculated using the definite integral of e^x. It concludes by reiterating the relationship between the height of the graph at a point x and the area under the curve up to that point, reinforcing the significance of e in both theoretical and applied mathematics.
Mindmap
Keywords
💡e
💡compound interest formula
💡natural logarithm
💡limit
💡exponential growth
💡derivative
💡area under the curve
💡factorial
💡calculus
💡Euler's number
💡infinite series
Highlights
The concept of 'e' is introduced as a significant mathematical constant.
The value of 'e' is approximately 2.718281828, with more digits following.
'e' is found in various areas of mathematics, including functions and logarithms.
The compound interest formula demonstrates how 'e' can be derived from continuous compounding.
As the number of compounding periods 'n' approaches infinity, the value of the compound interest formula approaches 'e'.
Another method to calculate 'e' is through the limit of (1 + 1/n)^(1/n) as 'n' approaches zero.
A table of values for different 'n' shows the approach to 'e' as 'n' gets smaller.
The sum of 1/n! from n=0 to infinity also converges to 'e'.
The function y = e^x has a unique property where its derivative is also e^x.
The area under the curve y = e^x from negative infinity to x equals the value of y at any point x.
The antiderivative of e^x is e^x + C, where C is a constant.
This presentation provides a comprehensive understanding of the mathematical constant 'e'.
The number 'e' has various applications in mathematics, making it a fundamental concept.
The derivation and calculation methods of 'e' are explained through practical examples.
The video aims to educate viewers on the importance and applications of the mathematical constant 'e'.
The concept of 'e' is explored through its historical, theoretical, and practical aspects.
The video provides a detailed explanation of how 'e' is used in the context of compound interest.
The video demonstrates the calculation of 'e' using various mathematical limits and series.
The video concludes by summarizing the value of 'e' and its applications in mathematics.
Transcripts
Browse More Related Video
14 - What is Euler's Number 'e', Ln(x) - Natural Log & e^x Functions?

Approximating functions with polynomials (part 3)

Deriving Functions with e!

Proof: d/dx(e^x) = e^x | Taking derivatives | Differential Calculus | Khan Academy

Calculus 2 Lecture 6.3: Derivatives and Integrals of Exponential Functions

Maclaurin series of e_ | Series | AP Calculus BC | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: