Deriving Functions with e!
TLDRThe video script provides an in-depth exploration of Euler's number, commonly known as 'e', and its significance in calculus and finance, particularly in the context of compounding interest. It begins by defining 'e' as a constant, approximately equal to 2.71828, and explains its various definitions, including the limit definition and its connection to compounded interest. The script then delves into the application of 'e' in business, especially in continuously compounded interest, and illustrates this with an example involving an account with a principal amount, interest rate, and time period. The discussion moves on to the calculus of 'e', demonstrating how to derive functions involving 'e' to the power of x, using the chain rule and providing several examples to solidify the concept. The video also covers the product and quotient rules when dealing with 'e' and concludes with an example of implicit differentiation and finding the equation of a tangent line to a function involving 'e'. The presenter emphasizes the importance of understanding 'e' not just as a constant but as a fundamental concept in calculus and its practical applications in finance.
Takeaways
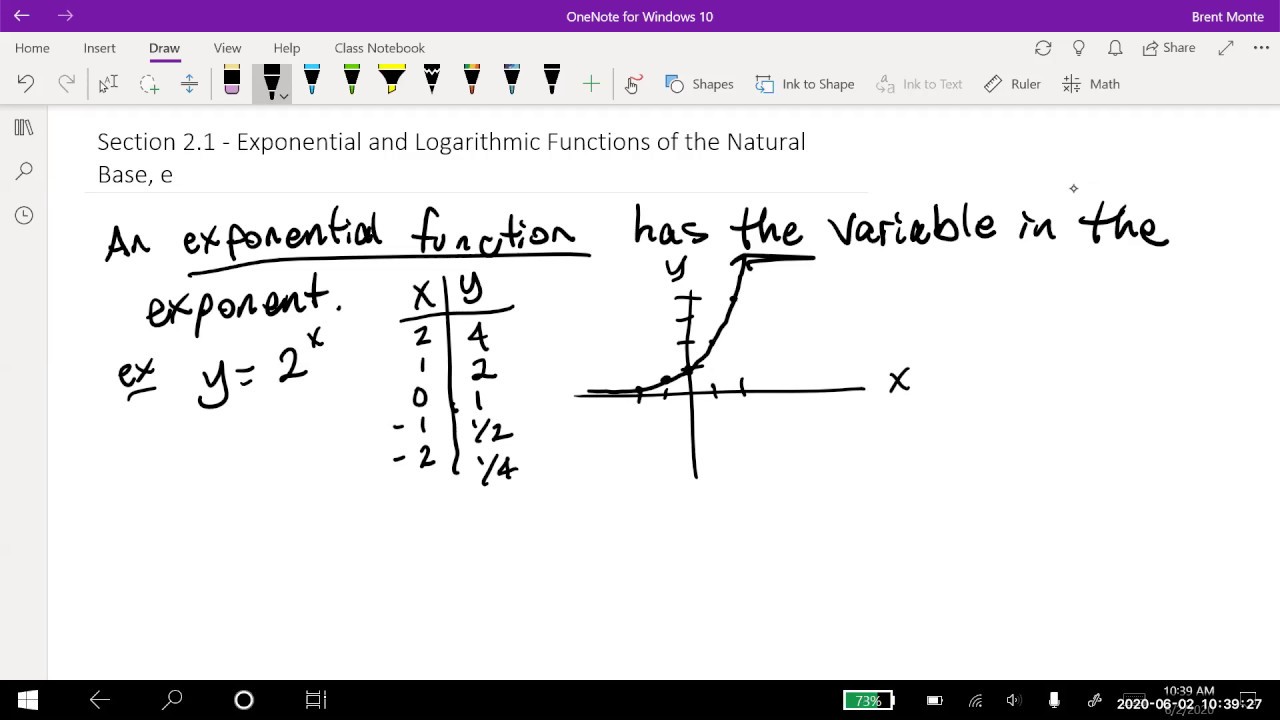
- 📐 The constant e, known as Euler's number, is similar to pi and is approximately equal to 2.71828.
- 🧮 e can be defined in multiple ways, including as the limit of (1 + 1/n)^n as n approaches infinity, which relates to the concept of compounded interest.
- 🏦 In the context of business, e is most famously used in the formula for continuously compounded interest, where A = P * e^(rT), known as the compound amount formula.
- 💰 An example of compound interest calculation is given, showing how to calculate the future value of an investment with a principal of $15,000, an interest rate of 8%, and a period of 30 years, compounded quarterly and continuously.
- 📈 The derivative of the function e^x is simply e^x, which is a direct result of the function's definition and is one of the simplest derivatives in calculus.
- ⛓ When dealing with a function of the form e^(g(x)), where g(x) is another function, the derivative is found by multiplying the derivative of g(x) by e^(g(x)), following the chain rule.
- 🔢 Constants behave the same way when multiplied by e^x; they are simply copied down in the derivative, similar to how constants are handled in other derivative rules.
- 🔄 The quotient rule and product rule are still applicable when differentiating functions involving e^x, and these rules are essential for more complex derivatives.
- 🌐 Implicit differentiation is used when the function is not explicitly given in terms of y or x, and it follows the same rules as regular differentiation, including the handling of e^x terms.
- 📉 The process for finding the equation of a tangent line to a curve at a specific point involves finding the derivative of the function at that point, which gives the slope of the tangent line.
- 📚 Memorizing the rule for differentiating e^(g(x)) is crucial, as it is a fundamental concept in calculus that builds upon the understanding of the chain rule and other basic differentiation rules.
Q & A
What is Euler's number (e) and how is it defined?
-Euler's number, commonly denoted as 'e', is a mathematical constant similar to pi (π). It can be defined in multiple ways, one of which is the limit as n approaches infinity of the function (1 + 1/n)^n. It is also associated with compounded interest and is approximately equal to 2.71828.
How is the concept of e related to compounding interest in business?
-The constant e is related to compounding interest through the formula for continuously compounded interest, which is A = P * e^(rT), where A is the amount of money accumulated after n years, including interest, P is the principal amount, r is the annual interest rate, and T is the time the money is invested or borrowed for, in years.
What is the formula for compounding interest when compounded quarterly?
-The formula for compounding interest when compounded quarterly is A = P * (1 + r/n)^(nT), where A is the amount of money accumulated, P is the principal amount, r is the annual interest rate, n is the number of times the interest is compounded per year (which is 4 for quarterly), and T is the time the money is invested or borrowed for, in years.
How much money will be in an account in 30 years if $15,000 is deposited with an 8% interest rate compounded quarterly?
-Using the compounding interest formula for quarterly compounding, the amount of money in the account after 30 years would be approximately $47,745.45.
What is the derivative of the function f(x) = e^x?
-The derivative of the function f(x) = e^x with respect to x is f'(x) = e^x, which means the derivative of an exponential function with base e is the same function.
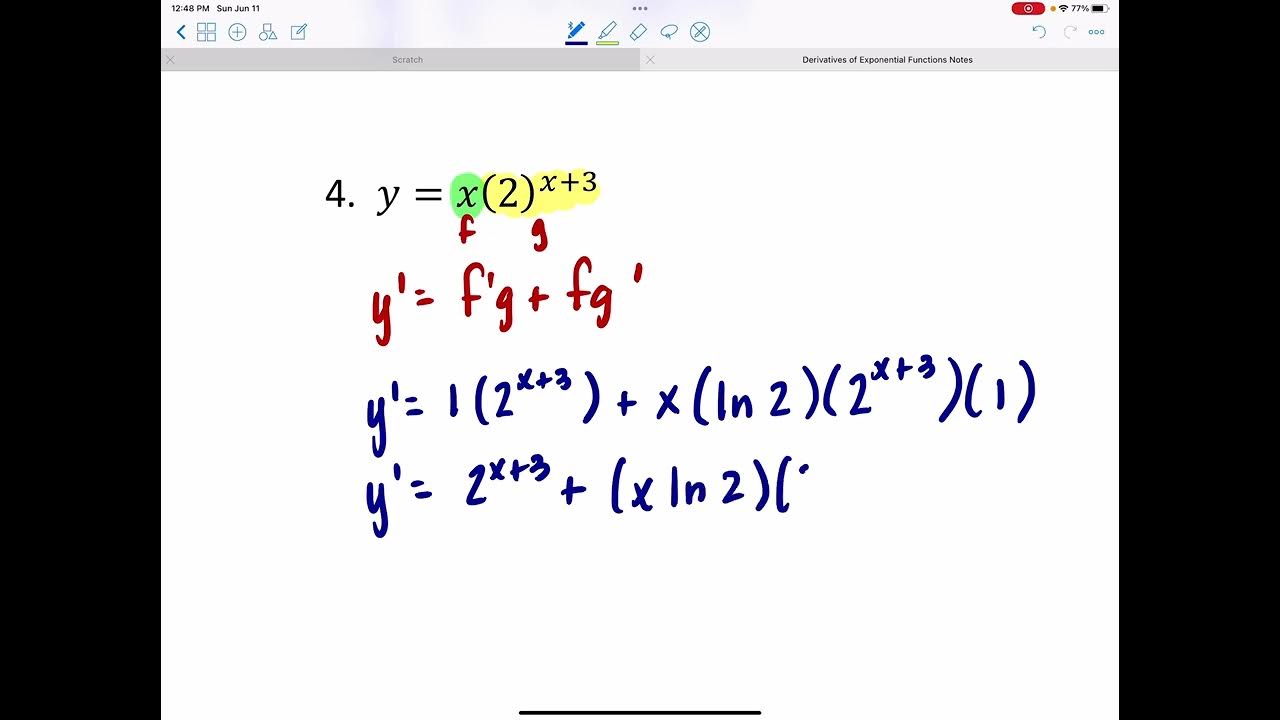
How do you find the derivative of a more complicated function involving e, such as y = e^(x^2 + 2x)?
-To find the derivative of y = e^(x^2 + 2x), you use the chain rule. The derivative is y' = e^(x^2 + 2x) * (2x + 2), which comes from multiplying the derivative of the power (2x + 2) by the original function e^(x^2 + 2x).
What is the derivative of a function that has e raised to a constant, such as 3e?
-The derivative of a function that has e raised to a constant, such as 3e, is 0 because e to a constant power is a constant, and the derivative of a constant is always 0.
How do you find the equation of the tangent line to the graph of the function f(x) = e^(3x - x^2) at the point (3,1)?
-To find the equation of the tangent line, first find the derivative f'(x) = e^(3x - x^2) * (3 - 2x). Then, evaluate the derivative at x = 3 to get the slope of the tangent line. After that, use the point-slope form of a line with the point (3,1) and the found slope to get the equation of the tangent line.
What is the general rule for differentiating a function of the form f(x) = e^(g(x)) where g(x) is another function of x?
-The general rule for differentiating a function of the form f(x) = e^(g(x)) is f'(x) = e^(g(x)) * g'(x), where g'(x) is the derivative of the function g(x).
How does the concept of e simplify the expression for continuously compounded interest?
-The concept of e simplifies the expression for continuously compounded interest by allowing the interest to be compounded an infinite number of times per year. This leads to the formula A = P * e^(rT), which is a direct consequence of taking the limit as the number of compounding periods per year approaches infinity.
What is the importance of understanding the derivative of e^x and its implications in calculus?
-Understanding the derivative of e^x is fundamental in calculus because it shows that the derivative of the exponential function with base e is the function itself. This property is unique to the base e and is used extensively in various calculus applications, including solving differential equations and understanding growth and decay processes.
Outlines
😀 Euler's Number and Compound Interest
This paragraph introduces Euler's number (e), a mathematical constant similar to pi, and explains its definition as the limit of (1 + 1/n)^n as n approaches infinity. It also touches on alternative definitions and its approximate value of 2.71828. The paragraph further explores e's relevance in the context of continuously compounded interest, illustrating how it can be used in business and finance through the formula A = P(1 + r/n)^(nt), where A is the amount of money accumulated after n years, including interest. An example calculation is provided for a $15,000 deposit at an 8% interest rate compounded quarterly for 30 years.
📈 Calculus of e^x and Derivatives
The second paragraph delves into the calculus of the exponential function e^x. It explains that the derivative of e^x with respect to x is simply e^x, a property that can be generalized using the chain rule for functions of the form e^(g(x)). Several examples are given to demonstrate how to apply this rule, including the derivation of e^(x^2 + 2x) and e^(-1/x^2). The paragraph also covers the product rule and quotient rule when dealing with more complex functions involving e, providing step-by-step derivations for clarity.
🔢 Derivatives of Functions Involving e
This paragraph continues the discussion on derivatives, focusing on more complex functions that involve e. It explains the process of differentiating functions such as e^(2x + 1) / e^(x - 1) and x * e^(-x) using the quotient rule and product rule, respectively. The paragraph emphasizes the importance of recognizing constants and applying the correct differentiation rules. It also touches on implicit differentiation with an example involving e^y and provides a detailed solution for finding dy/dx from a given equation.
📉 Implicit Differentiation and Tangent Lines
The fourth paragraph focuses on implicit differentiation and finding the equation of a tangent line to a function. It provides a step-by-step guide to differentiating an equation involving e^y and rearranging it to solve for dy/dx. The paragraph then presents a classic problem of finding the equation of a tangent line to the function f(x) = e^(3x - x^2) at the point (3,1). It outlines the process of finding the derivative, calculating the slope of the tangent line, and using the point-slope form to derive the equation of the tangent line.
🎓 Recap and Final Thoughts
The final paragraph recaps the key points discussed in the video. It reiterates the importance of understanding Euler's number (e) and its role in compound interest and calculus. The paragraph emphasizes the rule for differentiating functions of the form e^(g(x)) and the need to apply previous rules for product, quotient, and chain rules when differentiating more complex functions. It concludes by encouraging viewers to attempt homework problems and seek clarification on any questions they may have.
Mindmap
Keywords
💡Euler's number (e)
💡Compounding interest
💡Derivative
💡Chain rule
💡Product rule
💡Quotient rule
💡Implicit differentiation
💡Tangent line
💡Limit
💡Natural logarithm
💡Exponential function
Highlights
Introduction to the constant e (Euler's number) and its significance in mathematics and business.
Definition of e as the limit of (1 + 1/N)^N as N approaches infinity.
Alternative definition of e through the summation of 1/N! fractions.
Approximation of e as 2.71828 and its relation to pi.
Application of e in the context of continuously compounded interest.
Formula for compounding interest with different frequencies (yearly, monthly, daily, etc.)
Derivation of the formula for continuous compounding interest using e.
Example calculation of compound interest for a principal amount over 30 years with quarterly and continuous compounding.
Explanation of the calculus of e and its unique property of being its own derivative.
Derivation rules for functions involving e to the power of a linear term (e^(ax))
Chain rule application in deriving more complex functions involving e to the power of other functions (e^(f(x)))
Examples of deriving functions with e to the power of a quadratic term and other polynomial terms.
Explanation of the quotient rule and its application to functions involving division by e to the power of x.
Product rule application to functions involving multiplication by e to the power of x.
Implicit differentiation involving functions with e to the power of y.
Procedure for finding the equation of a tangent line to a graph involving e to the power of x.
Summary of the key rules for deriving functions involving e to the power of various expressions.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: