Properties of Limits
TLDRThis script teaches the application of limit properties to evaluate complex functions. It demonstrates how to calculate limits through multiplication, addition, and division of functions, as well as dealing with powers and roots. By using given limits of sample functions f(x) and g(x), the video illustrates step-by-step methods to simplify and compute the limits as x approaches a specific value, emphasizing the importance of showing work for clarity and correctness in mathematical problem-solving.
Takeaways
- 📝 The limit of a function can be evaluated using properties of limits.
- 🔢 When the limit of f(x) as x approaches 'a' is 4, and the limit of g(x) as x approaches 'a' is -3, the limit of 4f(x) as x approaches 'a' is 16.
- 📈 For a sum or difference of functions, like 3f(x) + 5g(x), the limit can be found by multiplying each function's coefficient by its respective limit and then adding or subtracting the results.
- 🤔 It's important to show your work when evaluating limits, even if the result seems intuitive.
- 🧠 The limit of a product of functions, f(x)g(x), is the product of their individual limits.
- 💡 When raising a function to a power or taking roots, like g(x)^4 or √f(x), the limit can be evaluated by applying the operation to each function's limit separately.
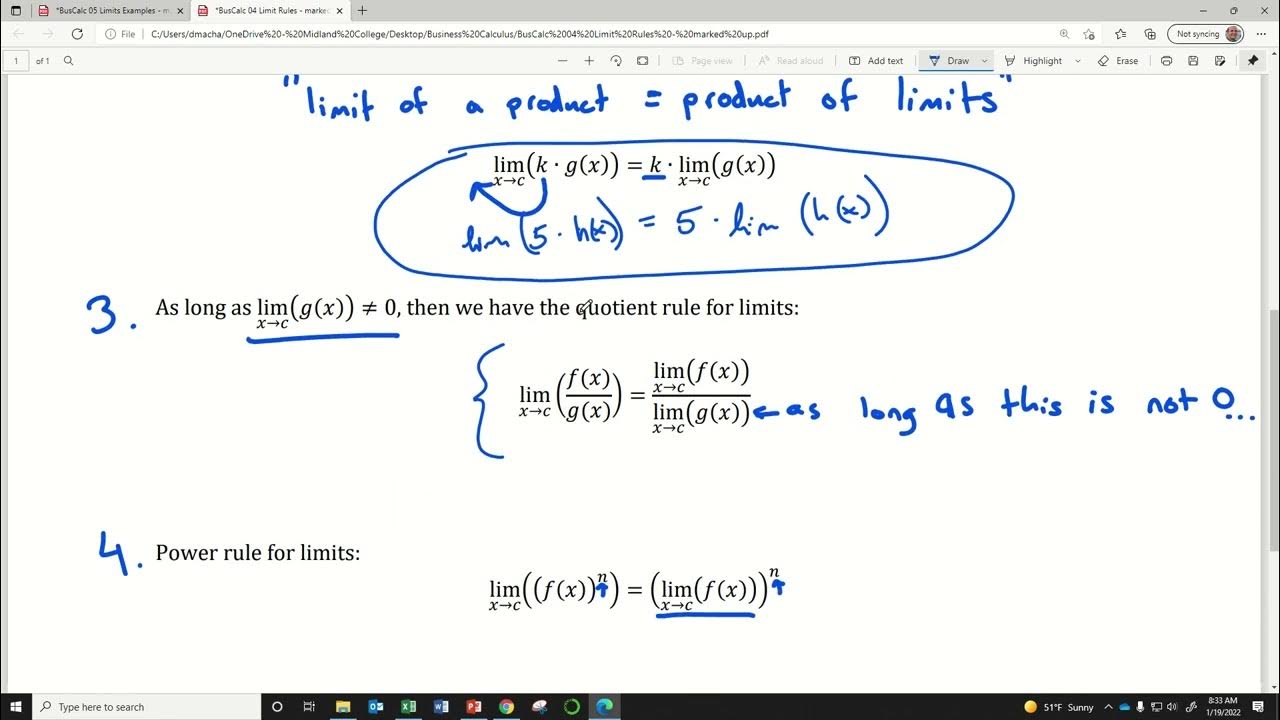
- 📊 The limit of a quotient of functions, f(x)/g(x), is the quotient of their individual limits, with the appropriate adjustments for negative signs.
- 🌟 Understanding and applying the properties of limits is crucial for solving problems in calculus.
- 📚 Practice is key to mastering the evaluation of limits using these properties.
- 🎓 Following the proper steps in limit evaluation is essential for clear communication of your process and results.
Q & A
What is the limit of a function and how is it denoted?
-The limit of a function is the value that the function approaches as the input (x) gets arbitrarily close to a certain point (a). It is denoted as `lim (x -> a) f(x)`, which reads 'limit of x趋向a时的f(x)'.
How can you evaluate the limit of a constant multiplied by a function using the properties of limits?
-When evaluating the limit of a constant multiplied by a function, you can take the constant out in front of the limit notation. For instance, the limit as x approaches a of 4 times f(x) is equal to 4 times the limit of f(x) as x approaches a.
What is the rule for evaluating the limit of a sum of two functions?
-To evaluate the limit of a sum of two functions, you can separate the functions and evaluate the limit of each function individually. Then, add the limits together. For example, the limit as x approaches a of [3f(x) + 5g(x)] is equal to [3 times the limit of f(x) as x approaches a] plus [5 times the limit of g(x) as x approaches a].
How do you find the limit of a product of two functions using limit properties?
-To find the limit of a product of two functions, you multiply the limit of each function individually and then combine the results. For instance, the limit as x approaches a of f(x) times g(x) is equal to the limit of f(x) as x approaches a times the limit of g(x) as x approaches a.
What is the process for evaluating the limit of a function raised to a power?
-To evaluate the limit of a function raised to a power, you raise the limit of the function to that power. For example, if the limit as x approaches a of g(x) is negative 3, then the limit as x approaches a of g(x) raised to the fourth power is (negative 3) to the fourth power.
How can you evaluate the limit of a function divided by another function?
-To evaluate the limit of a function divided by another function, you can separate the expression into the limit of the numerator and the limit of the denominator. For example, the limit as x approaches a of f(x) divided by g(x) is equal to the limit of f(x) as x approaches a times the reciprocal of the limit of g(x) as x approaches a.
What is the significance of showing your work when evaluating limits?
-Showing your work when evaluating limits is important because it demonstrates your understanding of the process and the properties of limits. It also allows others to follow your reasoning and check your calculations, ensuring accuracy and clarity in the evaluation.
What is the role of intuition in evaluating limits?
-Intuition can provide a quick sense of what the limit might be, but it is crucial to show the step-by-step process to validate your intuition. This ensures that the evaluation is mathematically sound and can be verified by others.
How does the limit of a function relate to the behavior of the function near a certain point?
-The limit of a function describes the behavior of the function near a certain point. It tells us the value that the function approaches as the input gets arbitrarily close to that point, without necessarily reaching it.
What is the limit as x approaches a of f(x)/1 over g(x)?
-The limit as x approaches a of f(x) divided by 1 over g(x) is simply the limit of f(x) as x approaches a divided by the limit of g(x) as x approaches a, provided g(x) is not zero at x=a to avoid division by zero.
How does the limit of a function affect its continuity?
-If the limit of a function as x approaches a certain point exists and is equal to the function's value at that point, then the function is continuous at that point. If the limit does not exist or is not equal to the function's value, the function is discontinuous at that point.
Outlines
📚 Introduction to Evaluating Limits using Properties
This paragraph introduces the concept of evaluating limits using properties of limits. It explains how to calculate the limit of a function as x approaches a certain value, given the limits of two functions f(x) and g(x). The paragraph demonstrates the process of evaluating the limit of 4f(x) when the limit of f(x) as x approaches a is 4, and similarly for the function g(x). It emphasizes the importance of showing work step by step, even when the result seems intuitive, and provides a clear example of how to do so.
Mindmap
Keywords
💡evaluate
💡limits
💡properties of limits
💡as x approaches a
💡function f(x)
💡function g(x)
💡constant
💡algebraic operations
💡rewrite
💡substitute
💡square root
💡division
Highlights
Evaluating limits using properties of limits is a fundamental skill in calculus.
When the limit of a function f(x) as x approaches a is 4, and the limit of g(x) as x approaches a is -3, the limit of 4f(x) as x approaches a is found by multiplying the constant 4 with the limit of f(x).
For the expression 3f(x) + 5g(x), the limit as x approaches a is calculated by multiplying the respective coefficients with the individual limits of f(x) and g(x), resulting in 12 - 15, which equals -3.
The product of f(x) and g(x), with limits of 4 and -3 respectively, results in a limit of -12 when x approaches a.
For the expression g(x)^4 * √f(x), the limit as x approaches a is found by raising the limit of g(x) to the fourth power and multiplying it by the square root of the limit of f(x), yielding a result of 162.
When evaluating the limit of f(x)/g(x) as x approaches a, the expression can be rewritten by separating f(x) and 1/g(x), resulting in 4 divided by -3, which equals -4/3.
Understanding the properties of limits allows for the simplification and evaluation of complex expressions involving multiple functions and operations.
The method of factoring out constants from functions in limits can simplify the evaluation process and clarify the result.
The sum of products in limits can be computed by multiplying the coefficients with the individual limits of the functions involved.
The product of limits can be found by multiplying the individual limits of the functions, as demonstrated with f(x) and g(x).
Raising a function to a power and then taking the root is a valid operation when evaluating limits, as seen with g(x)^4 * √f(x).
Dividing one function by another in limits is equivalent to multiplying the limit of the first function by the reciprocal of the limit of the second function.
The properties of limits provide a systematic approach to solving problems that involve the combination of multiple functions and constants.
The process of evaluating limits can be made more transparent by showing each step, which is often required in academic settings.
The concept of limits is crucial for understanding the behavior of functions as they approach certain values and is a cornerstone of calculus.
The examples provided in the transcript serve as a practical guide for students learning how to evaluate limits using the properties of limits.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: