What is Kinetic Energy & Work-Energy Theorem in Physics? - [1-8]
TLDRThis physics tutorial explores kinetic energy and the work-energy theorem, illustrating how work done on an object translates to its kinetic energy. It defines kinetic energy as \( \frac{1}{2}mv^2 \), explaining its dependence on mass and velocity. The video uses examples like a rolling baseball and a moving box to clarify concepts and introduces the work-energy theorem, which equates work done on a system to the change in its kinetic energy. It also solves problems involving calculating kinetic energy and applying the theorem to find work done without direct force or distance measurements.
Takeaways
- 📚 The script introduces the concept of kinetic energy (KE) and the work-energy theorem, fundamental topics in physics related to energy and work.
- 🚀 Kinetic energy is defined as \( \frac{1}{2} m v^2 \), where 'm' is the mass of the object and 'v' is its velocity. It measures the energy of motion.
- 🔢 The unit for both work and kinetic energy is the joule, indicating a direct relationship between the two concepts.
- 🔄 The work-energy theorem states that the work done on an object is equal to the change in its kinetic energy, highlighting the conservation of energy in a closed system.
- 🧩 The script uses a thought experiment involving a box being pushed to illustrate the connection between work done and the resulting kinetic energy.
- ⚡ It explains that kinetic energy is a form of energy associated with the motion of an object, distinct from other forms of energy like potential energy.
- 🎯 The work-energy theorem is applied to solve problems involving changes in kinetic energy due to work done on an object, without needing to know the exact force or distance involved.
- 📉 The script clarifies that at the highest point of a projectile's motion, only the horizontal component of velocity (which remains constant) is considered for calculating kinetic energy.
- 📚 It demonstrates problem-solving techniques using the work-energy theorem to find unknown quantities like velocity or work done, given changes in kinetic energy.
- 🔄 The concept of potential energy is previewed as another form of energy that, like kinetic energy, is measured in joules but represents stored energy due to an object's position.
- 📈 The script emphasizes the importance of understanding the relationship between work, kinetic energy, and the conservation of energy in various physical scenarios.
Q & A
What is the definition of kinetic energy in physics?
-In physics, specifically in classical motion, kinetic energy is defined as the energy an object possesses due to its motion. It is calculated using the formula KE = 1/2 * m * v^2, where 'm' is the mass of the object and 'v' is its velocity.
Why is the kinetic energy formula KE = 1/2 * m * v^2?
-The specific form of the kinetic energy formula is derived from empirical observations and the fundamental principles of physics. It accurately represents the energy of motion, although the exact reason for the 1/2 factor and the squaring of velocity is a result of how the universe operates.
What is the unit of kinetic energy?
-The unit of kinetic energy is the joule, which is the same unit used for work and potential energy in physics.
How is the concept of work related to kinetic energy?
-The work done on an object translates into a change in the object's kinetic energy. The work-energy theorem states that the work done on a system is equal to the change in the system's kinetic energy, which is the difference between the final and initial kinetic energies.
What is the work-energy theorem and how is it expressed mathematically?
-The work-energy theorem states that the net work done on an object is equal to the change in its kinetic energy. Mathematically, it is expressed as W = ΔKE = KE_final - KE_initial, where W is the work done, and KE_initial and KE_final are the initial and final kinetic energies, respectively.
Can you provide an example of how to calculate the kinetic energy of a baseball thrown at an angle?
-To calculate the kinetic energy of a baseball thrown at an angle, you first determine the horizontal component of the velocity at the highest point of its trajectory (where the vertical component is zero). Then, use the formula for kinetic energy with the mass of the baseball and the horizontal velocity squared, divided by 2.
What is the significance of the work-energy theorem in solving problems involving work and kinetic energy?
-The work-energy theorem allows us to calculate the work done on an object without knowing the force applied or the distance over which it was applied, as long as we know the initial and final kinetic energies of the object.
How can the kinetic energy of an object be determined if its velocity changes?
-The kinetic energy of an object can be determined by using the kinetic energy formula with the object's mass and its final velocity squared, divided by 2. If the initial velocity is known, the change in kinetic energy can be found by comparing the initial and final kinetic energy values.
What is the relationship between the mass of an object and its kinetic energy?
-The kinetic energy of an object is directly proportional to its mass. For a given velocity, an object with a larger mass will have more kinetic energy than an object with a smaller mass.
Can you explain how to find the velocity of a ping pong ball that has the same kinetic energy as a bowling ball?
-To find the velocity of a ping pong ball that has the same kinetic energy as a bowling ball, first calculate the kinetic energy of the bowling ball using its mass and velocity. Then, set the ping pong ball's kinetic energy equal to this value, solve for the ping pong ball's velocity squared by dividing the bowling ball's kinetic energy by half the mass of the ping pong ball, and then take the square root of the result.
Outlines
🚀 Introduction to Kinetic Energy and Work-Energy Theorem
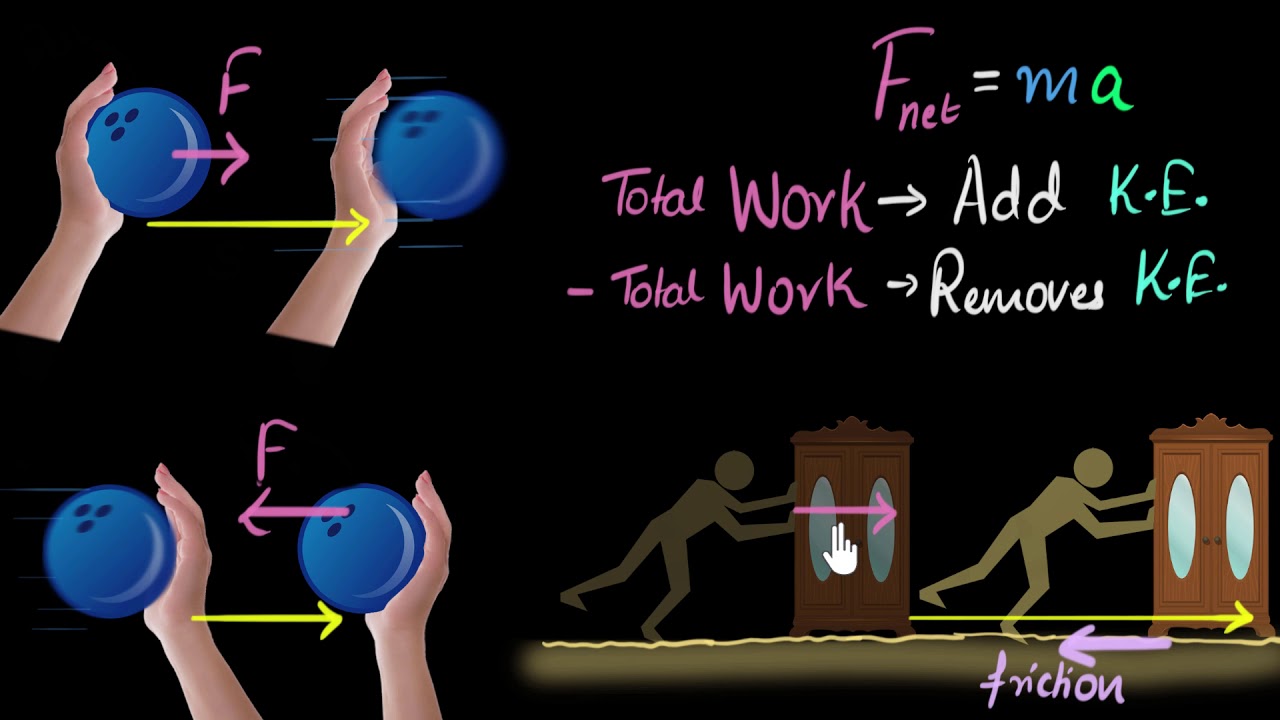
This paragraph introduces the fundamental concepts of kinetic energy and the work-energy theorem. It emphasizes the importance of understanding energy in physics, especially in real-world applications like roller coasters. The script explains kinetic energy (KE) with the formula KE = 1/2 * m * v^2, where m is mass and v is velocity. It also touches on the units of energy (joules) and how they relate to work, hinting at the connection between work done on an object and the change in its kinetic energy.
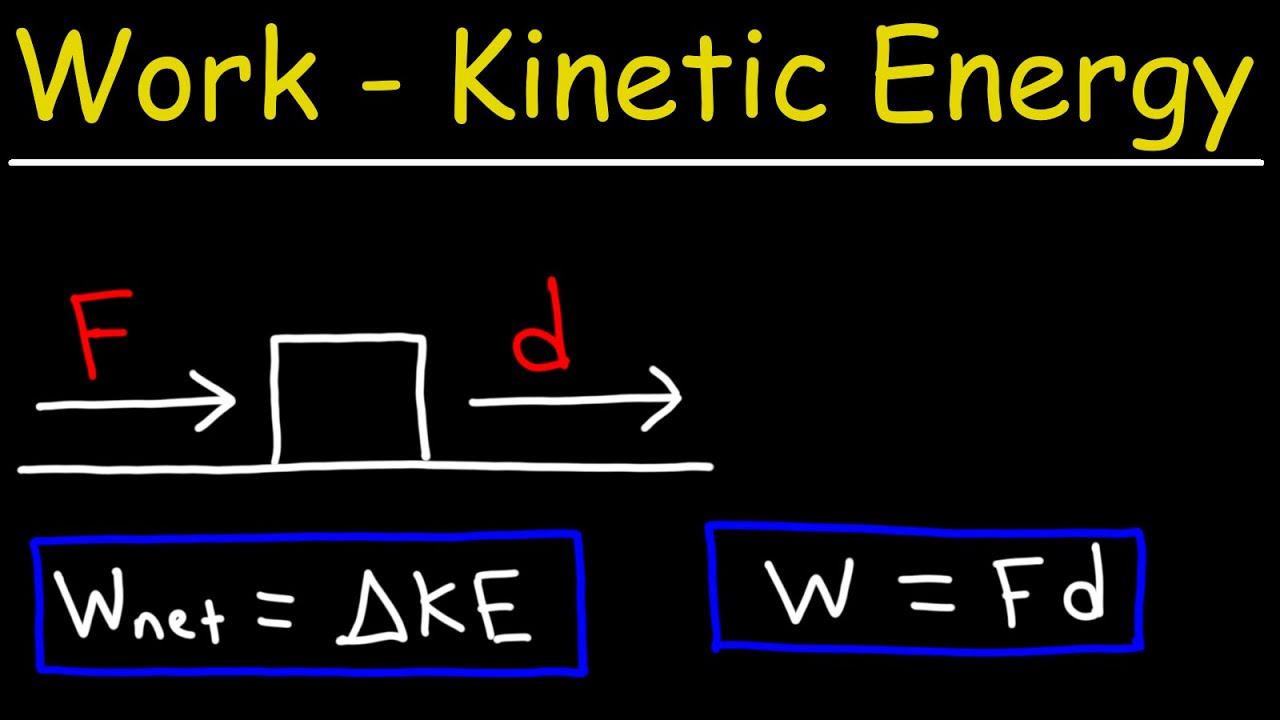
🔧 The Relationship Between Work and Kinetic Energy
The paragraph explores the relationship between the work done on an object and the resulting change in its kinetic energy. It uses the example of pushing a box to explain how force applied over a distance results in work, which in turn causes acceleration and an increase in the object's velocity. The script clarifies that the work done translates directly into an increase in kinetic energy, with the equation work = ΔKE (final KE - initial KE), highlighting the direct correlation between work (in joules) and the change in kinetic energy.
📚 The Work-Energy Theorem and its Applications
This section delves into the work-energy theorem, illustrating how the work done on a system equals the change in its kinetic energy. The script provides an example of a baseball thrown at an angle, calculating its kinetic energy at the highest point of its trajectory by considering only the horizontal component of its velocity. The explanation reinforces the theorem's principle that work done on an object results in an equivalent increase in kinetic energy.
📉 Calculating Kinetic Energy and Work with Variable Velocities
The paragraph presents a problem-solving approach to calculate kinetic energy and the work done on a particle moving from one point to another. It explains how to find the kinetic energy at different points using the kinetic energy formula and how to determine the velocity at a specific point given the kinetic energy. The script also demonstrates the application of the work-energy theorem to find the total work done on a particle without directly knowing the force or distance, emphasizing the theorem's utility in practical scenarios.
🎯 Comparing Kinetic Energies of Different Masses
This section examines the concept of equating the kinetic energies of two objects with vastly different masses—a bowling ball and a ping pong ball. The script guides through the calculation of the kinetic energy for the bowling ball and then sets up an equation to find the velocity of the ping pong ball that would result in the same kinetic energy. The process involves converting mass units and solving for the unknown velocity, revealing the much higher speed required for the lighter ping pong ball to match the kinetic energy of the heavier bowling ball.
🔄 Converting Units and Calculating Velocities for Equal Kinetic Energy
The final paragraph focuses on the unit conversion and the mathematical process of determining the velocity needed for the ping pong ball to have the same kinetic energy as the bowling ball. It emphasizes the importance of using consistent units in calculations and demonstrates the step-by-step procedure to find the required velocity, which turns out to be significantly higher for the ping pong ball due to its lower mass. This paragraph reinforces the understanding of kinetic energy, its dependence on mass and velocity, and the practical application of these concepts.
Mindmap
Keywords
💡Kinetic Energy
💡Work Energy Theorem
💡Work
💡Force
💡Joules
💡Mass
💡Velocity
💡Acceleration
💡Potential Energy
💡Newton's Second Law
Highlights
Introduction to the concept of kinetic energy and its importance in physics.
Explanation of kinetic energy equation, KE = 1/2 * m * v^2.
Discussion on the units of kinetic energy, which are joules, the same as work.
Illustration of the relationship between mass, velocity, and kinetic energy using a thought experiment with a box.
Introduction of the work-energy theorem and its connection to kinetic energy.
The work-energy theorem states that work done on an object translates into a change in its kinetic energy.
Problem-solving approach using the work-energy theorem to find kinetic energy at a baseball's highest point.
Calculation of horizontal velocity and its constancy in projectile motion.
Determination of kinetic energy at the highest point of a projectile's trajectory.
Use of the work-energy theorem to calculate the total work done on a particle without knowing force or distance.
Explanation of how to find the velocity at a second point given the kinetic energy.
Demonstration of calculating kinetic energy for different objects and comparing their speeds to achieve the same energy.
Conversion of mass units from grams to kilograms for consistent calculations in physics.
Concept that a smaller mass object must move faster to have the same kinetic energy as a larger mass object.
Final problem illustrating the application of kinetic energy principles to everyday objects like a bowling ball and a ping pong ball.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: