Work-Energy Theorem | Physics Animation
TLDRIn this educational video, Earthspan introduces the Work-Energy Theorem, explaining the relationship between work done on an object and its change in kinetic energy. The video provides a clear definition of work and energy, and demonstrates the theorem with examples, including calculating work done on a cart and determining its final kinetic energy and velocity. It also challenges viewers with a problem to calculate the work needed to accelerate a cart to a specific velocity, making the concept of work and energy both engaging and accessible.
Takeaways
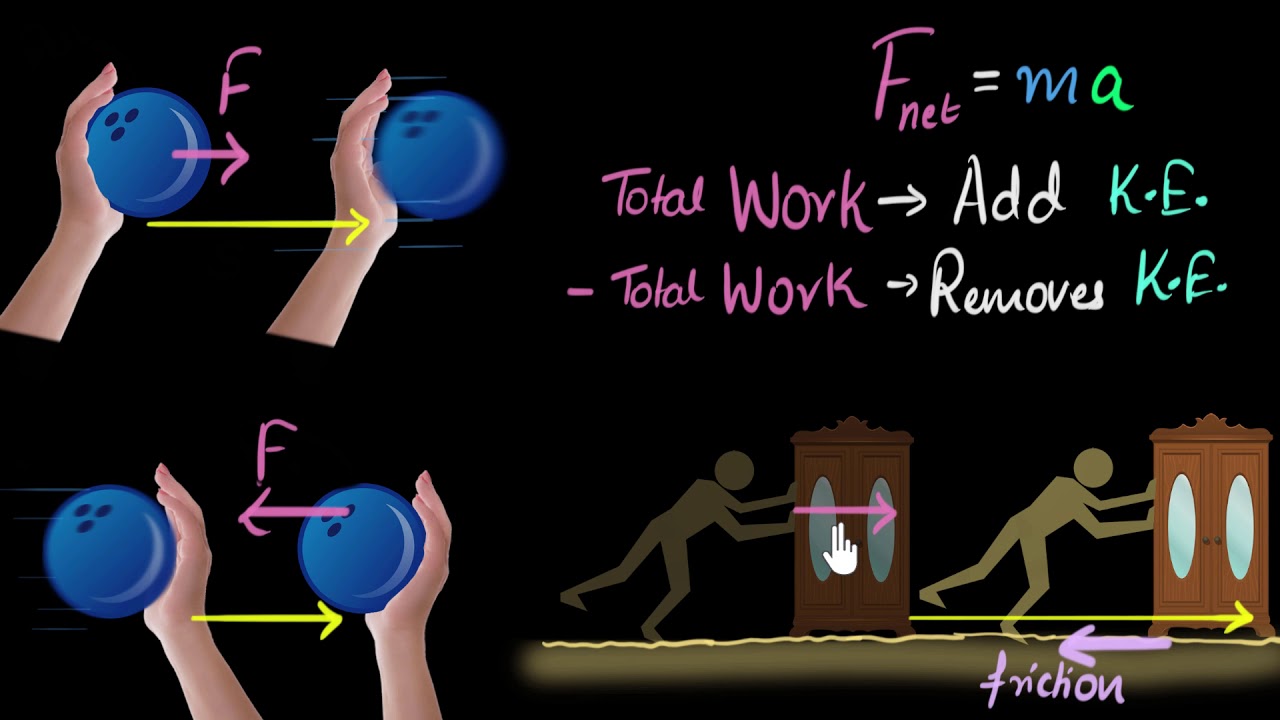
- 😀 The Work-Energy Theorem states that work done on an object results in a change in its kinetic energy.
- 🔍 Work is defined as the energy transferred by a force causing the displacement of an object.
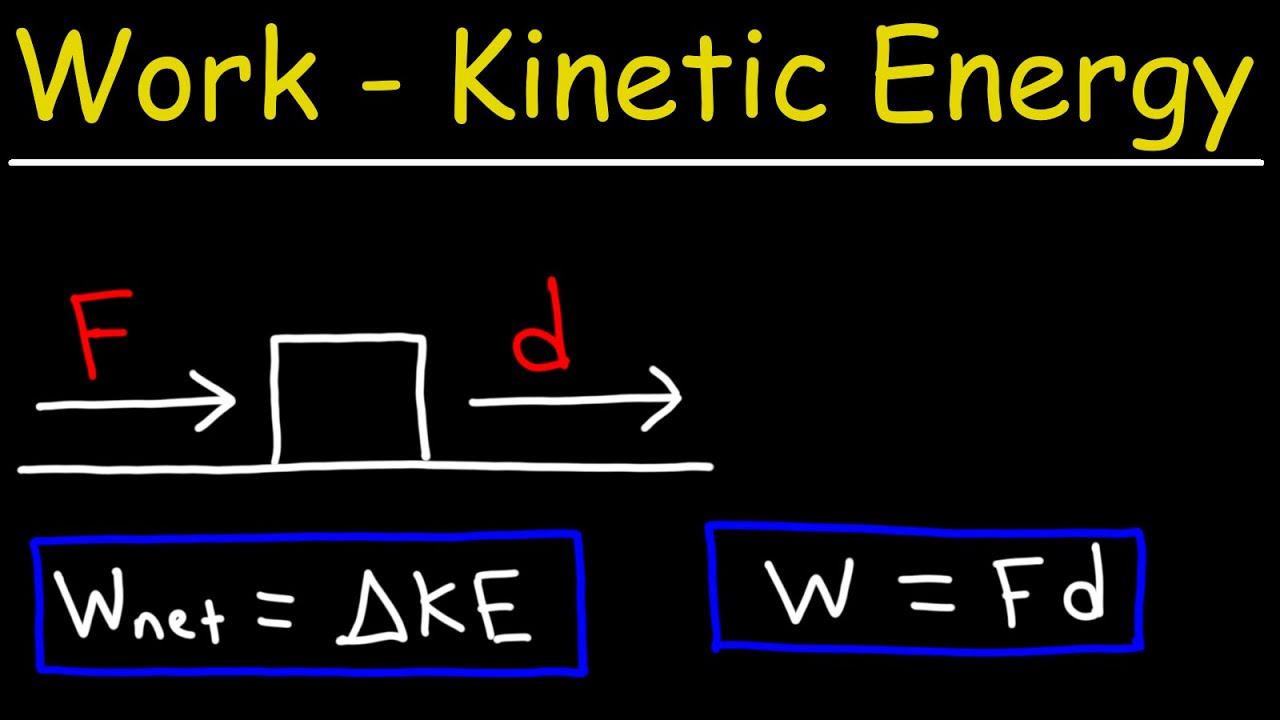
- 🔎 Energy is the capacity to do work, with work calculated as force times distance (W = F * d).
- 🚀 Kinetic energy is the energy of motion, calculated as one-half mass times velocity squared (KE = 0.5 * m * v²).
- 📚 The Work-Energy Theorem formula is Work = Final Kinetic Energy - Initial Kinetic Energy.
- 🛠️ An example in the script illustrates a 50 N force applied to a 20 kg cart, displacing it 150 meters on a frictionless surface.
- 🔢 The work done in the example is calculated to be 7500 joules (W = 50 N * 150 m).
- 🌟 Since the cart starts at rest, the initial kinetic energy is zero, making the final kinetic energy equal to the work done (7500 joules).
- 📉 The speed of the cart is found by rearranging the kinetic energy formula to solve for velocity (v = √(2 * Work / Mass)).
- 🔄 The second problem asks for the work required to accelerate a 20 kg cart from 20 m/s to 50 m/s, using the formula for net work (W_net = 0.5 * m * (v_f² - v_i²)).
- 🎯 The required work for the second problem is calculated to be 21,000 joules, demonstrating the application of the Work-Energy Theorem.
Q & A
What is the definition of work according to the video?
-Work is defined as the energy transferred by a force, which causes the displacement of an object.
How is work calculated in the context of the video?
-Work can be calculated using the formula work equals force times distance.
What is the definition of energy as presented in the video?
-Energy is simply defined as the capacity to do work.
What is the basic idea of the work energy theorem?
-The work energy theorem states that when work is done on an object, there will be a change in that object's kinetic energy.
What is kinetic energy?
-Kinetic energy is the energy of motion, and it is calculated as one-half mass times velocity squared.
In the example given, what is the force applied to the cart?
-A 50 newton force is applied horizontally to a 20 kilogram cart.
How much work is done by the force in the example provided?
-The work done by the force is 7500 joules, calculated as 50 newtons times 150 meters.
What is the final kinetic energy of the cart in the example?
-The final kinetic energy of the cart is 7500 joules, which is the same as the work done on it.
How can we find the speed of the cart after the force is applied?
-We can find the speed of the cart by using the work energy theorem and the formula for kinetic energy, rearranging it to solve for velocity.
In the second problem, what is the initial and final velocity of the cart?
-The initial velocity is 20 meters per second, and the final velocity is 50 meters per second.
How much work is required to accelerate a 20 kg cart from 20 m/s to 50 m/s?
-The required work is 21,000 joules, calculated using the formula for net work as the change in kinetic energy.
Outlines
🔧 Work and Energy Basics
The first paragraph introduces the concept of work and energy, defining work as the energy transferred by a force causing displacement and energy as the capacity to do work. It explains the formula for calculating work (force times distance) and sets the stage for the main topic, the Work-Energy Theorem. This theorem is described as a principle that equates work done on an object to the change in its kinetic energy, which is the energy of motion. A practical example is given involving a 50 Newton force applied to a 20 kg cart, calculating the work done and the final kinetic energy, leading to a discussion on how to determine the cart's speed after the work is done.
🚀 Applying the Work-Energy Theorem
The second paragraph delves into applying the Work-Energy Theorem with a specific problem involving accelerating a 20 kg cart from 20 m/s to 50 m/s. It outlines the process of calculating the required work using the theorem's formula, which involves the mass, initial velocity, and final velocity. The solution is presented, showing that the work needed is 21,000 joules. The paragraph concludes with an invitation for the viewer to engage with the material and a sign-off from the presenter, emphasizing the ease of learning with the channel.
Mindmap
Keywords
💡Work
💡Energy
💡Kinetic Energy
💡Displacement
💡Work-Energy Theorem
💡Force
💡Frictionless Surface
💡Velocity
💡Mass
💡Joules
💡Acceleration
Highlights
Introduction to the topic of the Work-Energy Theorem by EarthBen.
Recap on the definitions of work and energy, where work is the energy transferred by a force and energy is the capacity to do work.
Explanation of the formula for calculating work: Work = Force × Distance.
The Work-Energy Theorem states that work done on an object results in a change in its kinetic energy.
Kinetic energy is defined as one-half mass times velocity squared.
An example problem is introduced to illustrate the Work-Energy Theorem.
A 50 Newton force is applied horizontally to a 20 kg cart at rest on a frictionless surface for 50 meters.
Calculation of work done by the force using the formula: Work = 7500 Joules.
Application of the Work-Energy Theorem to find the final kinetic energy of the cart, which equals the work done.
The cart's initial kinetic energy is zero since it starts at rest.
Determination of the cart's final speed using the kinetic energy formula.
A second problem is presented to calculate the work required to accelerate a 20 kg cart from 20 m/s to 50 m/s.
Use of the formula for net work to calculate the required work: Work_net = 1/2 * mass * (velocity_final^2 - velocity_initial^2).
Calculation of the required work to accelerate the cart, resulting in 21,000 Joules.
Encouragement for viewers to pause the video and attempt the problem before the solution is revealed.
Conclusion of the video with a summary of the Work-Energy Theorem and a sign-off from EarthBen.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: