High School Physics - Coulomb's Law

Dan Fullerton
12 Dec 201108:51
EducationalLearning
32 Likes 10 Comments

TLDRIn this informative lecture, Mr. Fullerton introduces Coulomb's Law, explaining the electrical force between charged particles. He emphasizes the similarities between Coulomb's Law and Newton's Law of Universal Gravitation, highlighting the inverse-square relationship between force and distance. Through practical examples and calculations, he demonstrates how to apply the formula to solve problems involving electrostatic forces, comparing the attractive and repulsive interactions between charged objects. The lecture concludes with an interactive problem-solving segment, reinforcing the concepts discussed.

Takeaways
  • 📚 Coulomb's Law describes the electrostatic force between charged particles, stating that like charges repel and opposite charges attract.
  • 🔋 The magnitude of the electrostatic force depends on the charges of the objects and the distance between them, with a stronger force at closer distances.
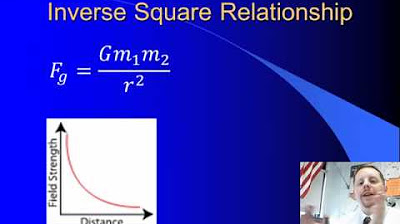
  • 📈 Coulomb's Law follows an inverse-square relationship, similar to the law of gravitation, where the force is proportional to 1/R^2, where R is the distance between the charged objects.
  • 🔧 The formula for electrostatic force (Fe) is given by Fe = k * (Q1 * Q2) / R^2, with k being the electrostatic constant (approximately 9 × 10^9 N m^2/C^2).
  • 🌐 The electrostatic constant (k) is different from the gravitational constant (G), with electricity being able to both attract and repel, whereas gravity only attracts.
  • 🤔 When calculating electrostatic force, the magnitude of the force is often of more concern than whether it's attractive or repulsive, as the nature of the charge (positive or negative) indicates the direction of the force.
  • 📊 Graphing Coulomb's Law shows a curve where the force is inversely proportional to the square of the distance, with the force decreasing rapidly as distance increases.
  • 🔄 The law can be applied to various scenarios, such as calculating the force between charged spheres, electrons in an electric field, and particles with given charges and distances.
  • 🧠 Understanding the relationship between charge, distance, and force is crucial for solving problems related to electrostatics and designing systems that utilize or counteract electrostatic forces.
  • 🔍 The law of gravitation and Coulomb's Law, while similar in form, have different constants and units, and their applications in physics are distinct, with gravity being a universal force and electrostatic force being a particle-specific interaction.
Q & A

  • What is Coulomb's Law and what does it describe?

    -Coulomb's Law describes the electrostatic force between charged particles. It states that like charges repel each other, while opposite charges attract. The magnitude of this force depends on the amount of charge on the objects and the distance between them, following an inverse-square relationship.

  • How does the magnitude of the electrostatic force depend on the charges and the distance between the charged objects?

    -The magnitude of the electrostatic force is directly proportional to the product of the charges (Q1 and Q2) and inversely proportional to the square of the distance (R) between them. This relationship is mathematically expressed as Fe = k * (Q1 * Q2) / R^2, where k is the electrostatic constant.

  • What is the electrostatic constant (k) in Coulomb's Law and what are its units?

    -The electrostatic constant (k) is approximately 9 x 10^9 Newton meter squared per Coulomb squared (N m^2/C^2). Sometimes it is also seen as 8.99 x 10^9 N m^2/C^2, which might be slightly more accurate.

  • How is Coulomb's Law similar to Newton's Law of Universal Gravitation?

    -Both Coulomb's Law and Newton's Law of Universal Gravitation have a similar form, with forces being proportional to the product of two quantities (charges or masses) and inversely proportional to the square of the distance between them. However, gravity only attracts and does not repel, while electrostatic force can both attract and repel.

  • What happens to the electrostatic force when the charge of one of the objects is increased?

    -As the charge of one of the objects increases, the electrostatic force also increases linearly because the force is directly proportional to the charges involved.

  • How does increasing the distance between two charged objects affect the electrostatic force?

    -When the distance between two charged objects is increased, the electrostatic force decreases because it is inversely proportional to the square of the distance. If the distance is tripled, for example, the force becomes one ninth of its original value.

  • What is the result of applying Coulomb's Law to find the force between three photons separated by one micron from a single electron?

    -The electrostatic force between the three photons and the single electron separated by one micron (1 x 10^-6 meters) is approximately -6.9 x 10^-16 Newtons. The negative sign indicates that the force is attractive because the charges are opposite.

  • What is the direction of the electrostatic force exerted on a beam of electrons between two oppositely charged parallel plates?

    -The electrostatic force exerted on the electrons by the field between two oppositely charged parallel plates is directed towards the top plate. This is because the electrons are negatively charged and feel an attractive force towards the positively charged top plate, and a repulsive force away from the negatively charged bottom plate, resulting in a net force towards the top.

  • In a sample problem, what is the electrostatic force between two charged particles with charges of 8 x 10^-19 Coulomb and 4.8 x 10^-19 Coulomb, separated by a distance of 1.2 x 10^-4 meters?

    -The electrostatic force between the two charged particles is approximately 2.4 x 10^-19 Newtons. This is calculated using Coulomb's Law: Fe = k * (Q1 * Q2) / R^2, where k is the electrostatic constant, Q1 and Q2 are the charges, and R is the distance between the particles.

  • How can the relationship between the magnitude of the electrostatic force and the distance between the centers of two charged particles be graphed?

    -The relationship can be graphed with the electrostatic force on the y-axis and the distance between the centers of the particles on the x-axis. Since it follows an inverse-square law, the graph will show a curve that is proportional to 1/R^2, where R is the distance between the particles.

  • What can we infer from the negative electrostatic force calculated in the example with three photons and a single electron?

    -A negative electrostatic force indicates that the force is attractive. This is because the force calculation takes into account the direction of the force as well as its magnitude. In the example, the negative sign indicates that the photons and the electron, having opposite charges, exert an attractive force on each other.

Outlines
00:00
📚 Introduction to Coulomb's Law and Comparison with Gravitational Law

This paragraph introduces the concept of Coulomb's Law, which describes the electrical force between charged particles. It outlines the objectives of the discussion, which include using Coulomb's Law to solve problems related to electrical force, recognizing that charged objects exert forces that can be both attractive and repulsive, and comparing and contrasting Newton's law of universal gravitation with Coulomb's Law. The explanation begins with the basics of Coulomb's Law, stating that like charges repel and opposite charges attract. The force of attraction or repulsion depends on the charge of the objects and the distance between them, with a stronger force as the objects are closer and a weaker force as they are further apart. This relationship is an inverse-square law, similar to the law of gravitation. The formula for electrical force (Fe) is introduced, which includes a constant (K), the charges (Q1 and Q2), and the square of the distance between the charges (R^2). The electrostatic constant (K) is provided, along with its value in Newton meter squared per Coulomb squared. The paragraph also discusses the similarities and differences between the gravitational force formula and the electrostatic force formula, noting that while gravity only attracts, electricity can both attract and repel, and the constants in each formula are different.

05:01
🔧 Applying Coulomb's Law in Calculations and Understanding the Electrostatic Force

This paragraph delves into the application of Coulomb's Law in calculations and the understanding of the electrostatic force. It begins with a practical example of calculating the electrostatic force between three photons and a single electron separated by a distance of one micron. The charges of the particles are given, and the force is calculated using Coulomb's Law. The concept of the magnitude of the force and its implications are discussed, noting that a negative force value indicates attraction due to opposite charges. The paragraph then presents a question about the change in gravitational and electrostatic forces when the distance between two charged spheres is increased to three meters. The explanation highlights the inverse-square law relationship, where tripling the distance results in the forces becoming one-ninth of their original values. Another question involves a beam of electrons in an electric field between two oppositely charged parallel plates, and the direction of the electrostatic force exerted on the electrons is discussed. The paragraph concludes with a sample problem involving the calculation of the electrostatic force between two charged particles and a graph illustrating the relationship between the magnitude of the electrostatic force and the distance between the particles' centers.

Mindmap
Keywords
💡Coulomb's Law
Coulomb's Law is a fundamental principle in physics that describes the electrostatic force between two charged particles. It states that like charges repel each other and opposite charges attract. The magnitude of this force depends on the amount of charge on each particle and the distance between them. In the video, Coulomb's Law is used to solve problems related to electrical forces and to compare it with Newton's law of universal gravitation, highlighting their similarities in inverse-square relationships.
💡Electrical Force
Electrical force is the force experienced by charged objects due to their electric charges. It can be either attractive or repulsive, depending on the nature of the charges involved. In the context of the video, electrical force is a central theme, with detailed discussions on how it can be calculated using Coulomb's Law and how it behaves with changes in charge and distance.
💡Charged Particles
Charged particles are particles that have an electric charge, either positive or negative. The presence of charge on these particles means they can interact with other charged particles through electrical forces. In the video, the concept of charged particles is crucial for understanding the application of Coulomb's Law, as the law is used to calculate the forces between such particles.
💡Inverse-Square Relationship
An inverse-square relationship is a mathematical concept where a physical quantity is proportional to the inverse square of another variable. In the context of the video, this relationship is used to describe how the electrostatic force and gravitational force decrease with the square of the distance between the interacting objects. This means that as the distance doubles, the force becomes one-fourth of the original value.
💡Electrostatic Constant (K)
The electrostatic constant, often denoted as K, is a constant of proportionality that appears in Coulomb's Law. It has a value of 9 x 10^9 N m^2/C^2, which is used to calculate the magnitude of the electrostatic force between two charged particles. The constant is a fundamental part of the law, allowing for the quantitative analysis of electrical forces in physics.
💡Newton's Law of Universal Gravitation
Newton's Law of Universal Gravitation is a fundamental principle that describes the gravitational force between two masses. It states that every point mass attracts every other point mass by a force acting along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them. In the video, this law is compared with Coulomb's Law to highlight the similarities in their mathematical forms and inverse-square relationships, although they describe different types of forces (gravitational vs. electrostatic).
💡Gravitational Force
Gravitational force is the attractive force that acts between all objects with mass. It is described by Newton's Law of Universal Gravitation, which states that the force is proportional to the product of the two masses and inversely proportional to the square of the distance between their centers. Unlike electrical forces, gravitational forces only attract and do not repel.
💡Electrostatic Force
Electrostatic force is the force that results from the interaction between charged objects. It can be either attractive or repulsive, depending on the types of charges involved. The magnitude of this force is governed by Coulomb's Law, which takes into account the charges of the objects and the distance between them.
💡Distance
In the context of the video, distance refers to the spatial separation between two charged particles or objects. The distance is a crucial factor in determining the magnitude of the electrostatic and gravitational forces between them, as both forces are inversely proportional to the square of the distance.
💡Attractive and Repulsive Forces
Attractive and repulsive forces are two types of interactions that can occur between objects or particles. Attractive forces pull objects together, while repulsive forces push them apart. In the video, these concepts are discussed in relation to charged particles, where like charges exert repulsive forces and opposite charges exert attractive forces.
💡Calculations
Calculations in the context of the video refer to the mathematical procedures used to determine the magnitude of electrostatic forces between charged particles. These calculations are based on the values of the charges, the distance between them, and the electrostatic constant, as described by Coulomb's Law.
Highlights

Coulomb's law is discussed as the electrical force between charged particles.

The law helps to solve problems related to electrical force and recognizes that charged objects exert attractive and repulsive forces.

A comparison is made between Newton's law of universal gravitation and Coulomb's law, highlighting their similarities.

Like charges repel and opposite charges attract according to Coulomb's law.

The magnitude of the electrostatic force depends on the charge of the objects and the distance between them.

An inverse-square relationship exists between the force and the distance, similar to the law of gravitation.

The formula for electrical force is given as Fe = k * (Q1 * Q2) / R^2, with k being the electrostatic constant.

The electrostatic constant k is approximately 9 * 10^9 N m^2/C^2.

Graphing Coulomb's law shows the effect of increasing charge and the relationship between force and distance.

Both gravity and electrostatic force follow an inverse-square law, but electricity can both attract and repel, unlike gravity.

The gravitational constant is 7 * 10^-11 N m^2/kg^2, differing in form from the electrostatic constant.

A practical example involves calculating the electrostatic force between three photons separated by a distance of one micron.

The force between two charged spheres is inversely proportional to the square of the distance between them.

A beam of electrons in an electric field between charged parallel plates will experience a net force towards the positive charge.

A sample problem calculates the electrostatic force between two particles with given charges and distance.

A graph of the electrostatic force against the distance between particle centers illustrates the inverse-square law relationship.

The lecture aims to provide a foundational understanding of Coulomb's law and its application to problems involving electrostatic force.

For further questions and help, resources like eight plus physics are recommended.

Transcripts

Browse More Related Video

Introduction to Coulomb's Law or the Electric Force

High School Physics - Newton's Law of Universal Gravitation

Calculating the Electric Force

Coulomb's Law - Net Electric Force & Point Charges

Coulomb's Law | Electrostatics | Electrical engineering | Khan Academy

Electric Charge: Crash Course Physics #25

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Coulomb's LawElectrical ForcesGravitational ComparisonPhysics EducationCharged ParticlesInverse-Square LawElectrostaticsProblem SolvingEducational ContentScientific Concepts