Coulomb's Law - Net Electric Force & Point Charges
TLDRThe video script delves into the fundamental concepts of Coulomb's Law, explaining the interactions between charged particles. It begins by discussing the structure of an atom, highlighting the roles of protons, neutrons, and electrons, and introduces the concept of quantized electric charge. The script then presents Coulomb's Law, detailing how the force between two point charges depends on their magnitudes and the distance between them. Through a series of examples and practice problems, the video illustrates the calculation of electric force and the determination of net electric charge in various scenarios, reinforcing the principles of electrostatics and their applications.
Takeaways
- 🔋 Coulomb's Law describes the electrostatic force between two point charges, with the force being directly proportional to the product of the magnitudes of the charges and inversely proportional to the square of the distance between them.
- ⚛️ The fundamental unit of electric charge is the coulomb, with a proton having a charge of +1.6 × 10^-19 coulombs and an electron having a charge of -1.6 × 10^-19 coulombs.
- 💥 Opposite charges attract while like charges repel; the force between charges can be calculated using Coulomb's Law: F = k * (q1 * q2) / r^2, where k is the electrostatic constant, q1 and q2 are the charges, and r is the distance between the centers of the charges.
- 📈 The electrostatic constant, k, is equal to 9 × 10^9 N m^2 C^-2, which is also equivalent to 1/(4πε₀), where ε₀ is the permittivity of free space (8.85 × 10^-12 F m^-1).
- 🔄 If the magnitude of one of the charges is doubled, the force between the charges also doubles; if the distance between the charges is doubled, the force is reduced to a quarter of its original value.
- 📏 The unit of force is the newton (N), and the unit of electric charge is the coulomb (C). Distance measurements in problems are typically in meters, with conversions from centimeters to meters as necessary.
- 🤔 When an object has a net positive charge, it contains more protons than electrons; if it has a net negative charge, it has more electrons than protons; a neutral object has equal numbers of protons and electrons.
- 📚 To solve problems, it's crucial to understand the direction of the electric force (attraction or repulsion) and to perform calculations with care regarding the sign of charges and the conversion of units.
- 🔧 Practice problems are essential for understanding the application of Coulomb's Law, and they often involve calculating the force between charges, the distance between charges, or the magnitude of charges given certain conditions.
- 🌐 The electric force is a vector quantity, having both magnitude and direction; however, when only the magnitude is needed, the direction can be ignored, as in the case of calculating the net force on a charge.
Q & A
What is the fundamental unit of electric charge, and how is it quantized?
-The fundamental unit of electric charge is the charge of a proton, which is 1.6 times 10 to the negative 19 coulombs. Electric charge is quantized, meaning it exists in discrete amounts, and always is a multiple of this fundamental value.
What are the basic properties of protons, neutrons, and electrons in an atom?
-Protons carry a positive charge, neutrons are neutral (uncharged), and electrons carry a negative charge. The nucleus of an atom contains protons and neutrons, while electrons orbit around the nucleus.
What does Coulomb's Law describe and how is it formulated?
-Coulomb's Law describes the electrostatic force between two point charges. It is formulated as the electric force being equal to the proportionality constant k, times the product of the magnitudes of charges q1 and q2, divided by the square of the distance r between the centers of the two charges.
What is the value of the proportionality constant k in Coulomb's Law and what units are associated with it?
-The proportionality constant k in Coulomb's Law is equal to 9 times 10 to the 9 newtons over square meters times square coulombs. It is also equal to 1 over four pi times the permittivity of free space, epsilon naught, which is approximately 8.85 times 10 to the negative 12 farads per meter.
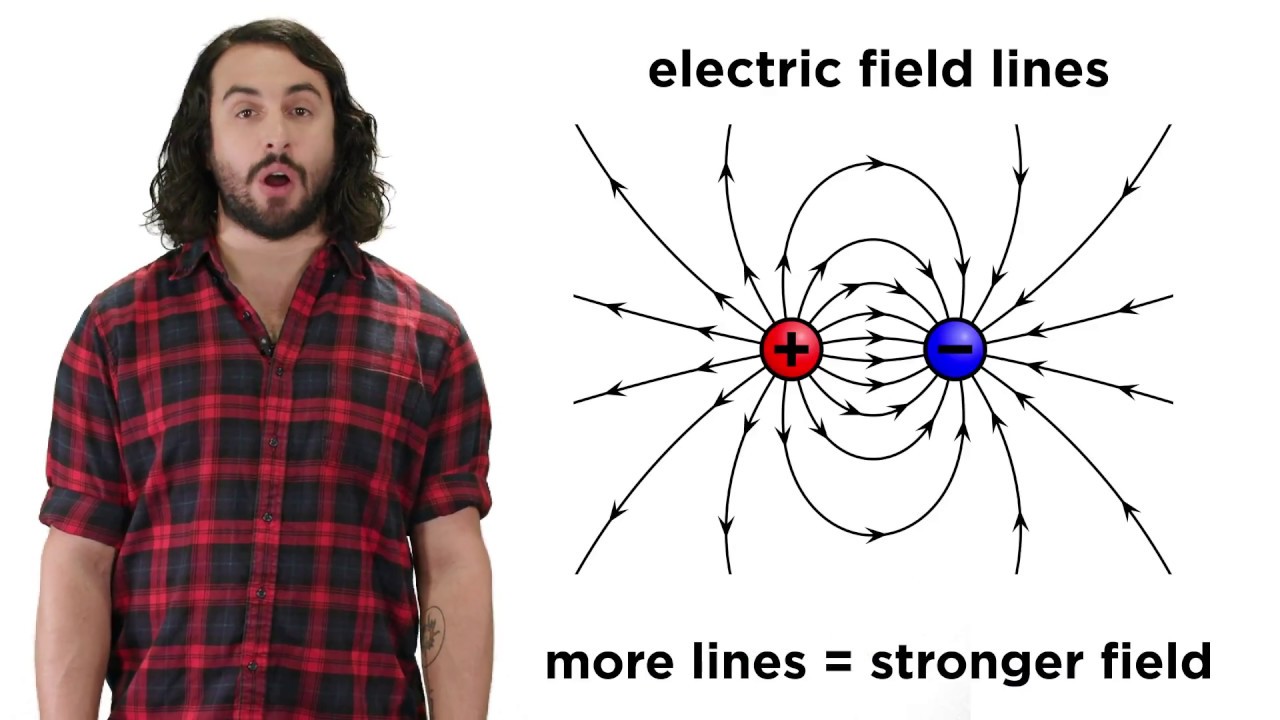
How do like and opposite charges interact according to Coulomb's Law?
-According to Coulomb's Law, like charges repel each other, while opposite charges attract each other. The forces between the charges are equal in magnitude but opposite in direction.
How does the electric force between two charges change if the magnitude of one charge is doubled?
-If the magnitude of one of the charges is doubled, the electric force between them will also double, as the force is directly proportional to the product of the magnitudes of the charges.
What happens to the electric force if the distance between two charges is doubled?
-If the distance between two charges is doubled, the electric force will be reduced to a quarter (one-fourth) of its original value, as the force is inversely proportional to the square of the distance between the charges.
What are the units for the charge in Coulomb's Law and how are they represented?
-The unit for charge in Coulomb's Law is the coulomb. Common subunits include the microcoulomb (1 times 10 to the minus 6 coulombs), milli coulomb (1 times 10 to the negative 3 coulombs), and nanocoulomb (1 times 10 to the negative 9 coulombs).
How can you calculate the net electric force acting on a charge due to multiple other charges?
-To calculate the net electric force on a charge due to multiple others, you calculate the individual forces between the charge in question and each of the other charges, taking into account their direction, and then sum these forces. If the forces are along the same line, you can simply add or subtract them based on their direction to find the net force.
Given a charge of -70 microcoulombs, how many electrons does it represent?
-A charge of -70 microcoulombs represents 4.375 times 10 to the 14 electrons. This is calculated by dividing the charge in coulombs by the charge of a single electron (-1.6 times 10 to the negative 19 coulombs).
What is the net electric charge on a metal sphere with 4.3 times 10 to the 21 protons and 6.8 times 10 to the 21 electrons?
-The net electric charge on the metal sphere is -400 coulombs. This is calculated by taking the difference between the number of electrons and protons, multiplying by the charge of a single proton (1.6 times 10 to the negative 19 coulombs).
Outlines
🔬 Introduction to Coulomb's Law and Atomic Structure
This paragraph introduces the concept of Coulomb's Law and the structure of an atom. It explains that atoms consist of a nucleus containing protons and neutrons, with electrons orbiting around it. Protons carry a positive charge, neutrons are neutral, and electrons carry a negative charge. The fundamental unit of electric charge is quantized and represented by the charge of a proton, which is 1.6 times 10 to the negative 19 coulombs. The paragraph sets the stage for understanding the interactions between charges and how they will be explored through Coulomb's Law.
📐 Mathematical Explanation of Coulomb's Law
This paragraph delves into the mathematical aspect of Coulomb's Law, describing the relationship between electric force, the magnitude of charges, and the distance between them. It explains how increasing the magnitude of a charge affects the electric force and how changing the distance between charges influences this force inversely. The constant 'k' in Coulomb's Law is introduced, with its value and significance in calculations highlighted. The paragraph also covers the units associated with the law, such as newtons for force and coulombs for charge, and the importance of using consistent units in calculations.
🔧 Working with Coulomb's Law: Practice Problems
The paragraph presents a series of practice problems to apply Coulomb's Law. It begins with a scenario involving a positive and a negative charge and explains the attractive force between them. The calculation of the electric force between two point charges of given magnitudes and distances is demonstrated. The concept of like charges repelling each other is also discussed, with an example of positive charges being pushed apart. The paragraph aims to solidify the understanding of how to use Coulomb's Law to calculate the forces between charges.
🧮 Solving Coulomb's Law Problems with Given Quantities
This paragraph continues with the practice problems, focusing on calculating the distance between charges when the force and charge magnitudes are known. It explains the process of isolating the variable of interest in Coulomb's Law equation and using it to find the unknown quantity. The paragraph provides a detailed walkthrough of the calculations, including the necessary unit conversions and the application of the law. It emphasizes the importance of understanding the direction of forces and how to handle like charges in calculations.
🔍 Further Analysis of Charge Quantities and Coulomb's Law
The paragraph explores the representation of charge quantities in terms of electrons and protons, and how to convert between these fundamental particles and electric charge. It presents problems involving the calculation of the number of electrons or protons corresponding to a given charge, and vice versa. The conversion between micro coulombs and fundamental charges, as well as the calculation of net electric charge on objects, are discussed. The paragraph reinforces the understanding of electric charge as a quantized property and its implications in physical scenarios.
📐 Calculating Net Electric Charge and Forces on Multiple Charges
This paragraph discusses the calculation of net electric charge on a metal sphere with an excess of electrons and the determination of the net electric force acting on charges placed at specific positions. It explains how to find the net charge by comparing the number of protons and electrons and how to calculate the force between identical charges. The concept of vector addition is introduced to find the net force when multiple forces act on a single charge. The paragraph provides a comprehensive understanding of how to deal with multiple charges and their interactions in the context of Coulomb's Law.
🌐 Application of Coulomb's Law: Electric Forces in a System of Charges
The final paragraph of the script applies Coulomb's Law to a system of three charges placed at different locations. It explains how to calculate the individual forces acting on each charge and then determine the net force experienced by each charge. The concept of vector addition is used to combine the forces acting in the same direction, and the calculation of net forces acting in opposite directions is demonstrated. The paragraph concludes with the net forces on two charges, providing a clear example of how to analyze and solve complex problems involving multiple charges and their interactions.
Mindmap
Keywords
💡Coulomb's Law
💡Nucleus
💡Protons
💡Electrons
💡Charge Quantization
💡Electric Force
💡Point Charges
💡Proportionality Constant (k)
💡Permittivity of Free Space
💡Net Charge
💡Unit Conversion
Highlights
Coulomb's Law is discussed in detail, providing a fundamental understanding of the electric force between charges.
The structure of an atom is explained, highlighting the roles of protons, neutrons, and electrons in determining electric charge.
Quantization of electric charge is introduced, emphasizing that charge exists in discrete amounts based on the fundamental value of charge.
The concept of point charges is defined, where the size of the charge is irrelevant, and only the magnitude and distance matter.
The equation for Coulomb's Law is presented, detailing the relationship between electric force, magnitude of charges, and the distance between them.
The proportionality constant 'k' in Coulomb's Law is explained, with its value and significance in calculations.
The effect of like and opposite charges on each other is discussed, with examples of attraction and repulsion.
The impact of increasing the magnitude of charges on the electric force is explored, showing a direct relationship.
The effect of increasing the distance between charges on the electric force is examined, highlighting an inverse square relationship.
The units associated with Coulomb's Law are detailed, including newtons for force and coulombs for electric charge.
A practical problem involving the calculation of electric force between two point charges of different signs is solved.
The method for calculating the distance between two point charges when the force and charges are known is demonstrated.
The calculation of the magnitude of two identical point charges given the force and distance is explained.
The conversion of electric charge to the number of electrons is illustrated, providing a link between charge and fundamental particles.
The calculation of electric charge from the number of protons is shown, highlighting the charge quantization.
The determination of net electric charge on a metal sphere with different numbers of protons and electrons is discussed.
A complex problem involving the net electric force on charges placed at different locations is solved.
The calculation of net electric force acting on individual charges in a scenario with multiple charges is demonstrated.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: