High School Physics - Ramps and Inclines
TLDRThe video script provides a comprehensive guide on analyzing scenarios involving objects on ramps or inclines. It emphasizes the importance of drawing and labeling free body diagrams, creating pseudo free body diagrams to align forces with coordinate axes, and applying Newton's laws of motion for problem-solving. The script walks through multiple examples, demonstrating how to calculate forces such as friction and normal forces, and how to determine the magnitude of external forces required to maintain static equilibrium on an inclined plane.
Takeaways
- 📝 The primary objective is to analyze situations involving objects on ramps or inclines using free body diagrams and Newton's laws of motion.
- 🎯 Start by drawing a free body diagram that labels all forces acting on the object at rest on the ramp, including friction, normal force, and weight.
- 🔍 When forces do not align with the axes, create a pseudo free body diagram to break forces into components along the x and y axes using trigonometry.
- 📐 Use the formulas mg sine-theta for the parallel component and mg cos-theta for the perpendicular component to break down the weight force in the pseudo free body diagram.
- 🔄 Newton's second law is applied to analyze the forces in both the x and y directions, considering the net force and the object's acceleration.
- ⚖️ In static equilibrium, where the net force is zero and there is no acceleration, the forces are balanced, allowing for problem-solving using the pseudo free body diagram.
- 🔢 Solve for unknown forces by setting up equations based on the net force in the respective direction and equating it to the mass times the acceleration.
- 🛣️ When dealing with inclined planes, the angle of inclination (theta) is crucial for determining the components of the gravitational force acting on the object.
- 📌 For objects in constant velocity motion (U), the net force is also zero, indicating static equilibrium, which can be used to find the magnitude of forces like pulling force F.
- 📋 The process involves drawing the free body diagram, creating a pseudo free body diagram for non-axial forces, and then applying Newton's second law to find unknown values.
- 🎓 Understanding and applying these concepts systematically helps in solving a variety of problems involving objects on ramps or inclines.
Q & A
What is the primary objective when analyzing situations involving objects on ramps or inclines?
-The primary objective is to draw and label a free body diagram showing all the forces acting on the object, then use Newton's laws of motion to solve problems related to the object's behavior on the ramp.
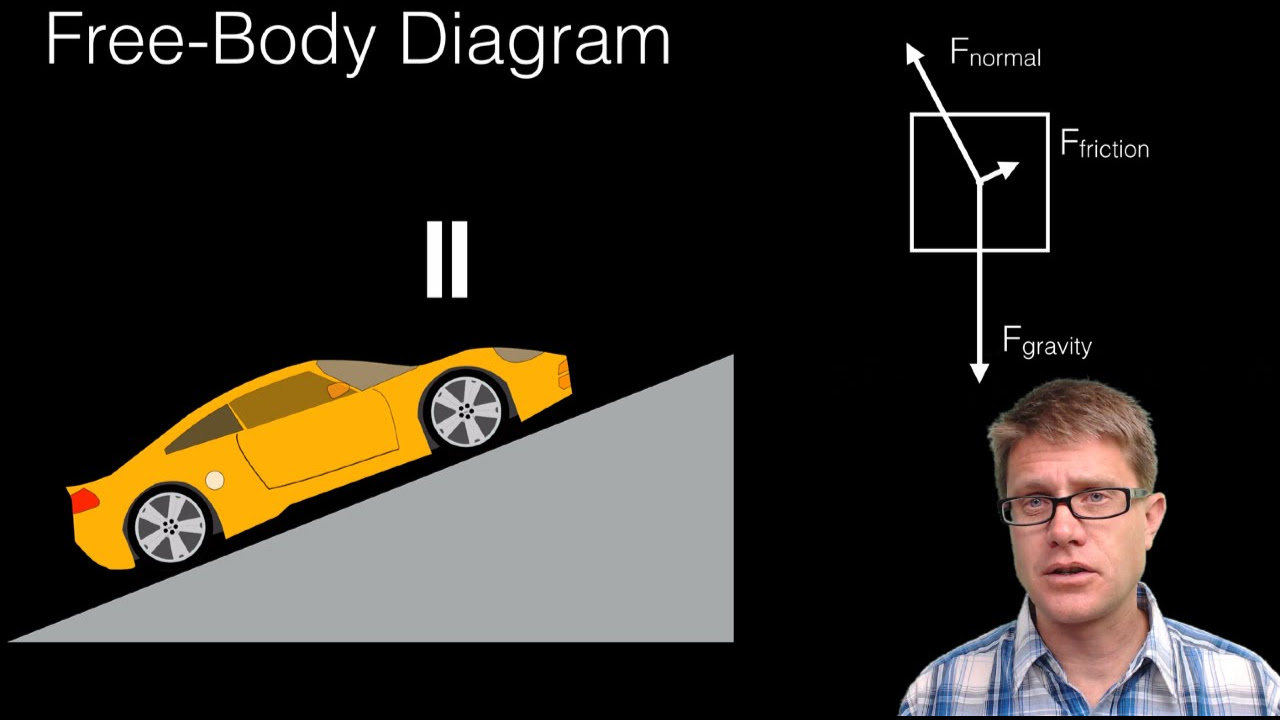
What is a free body diagram?
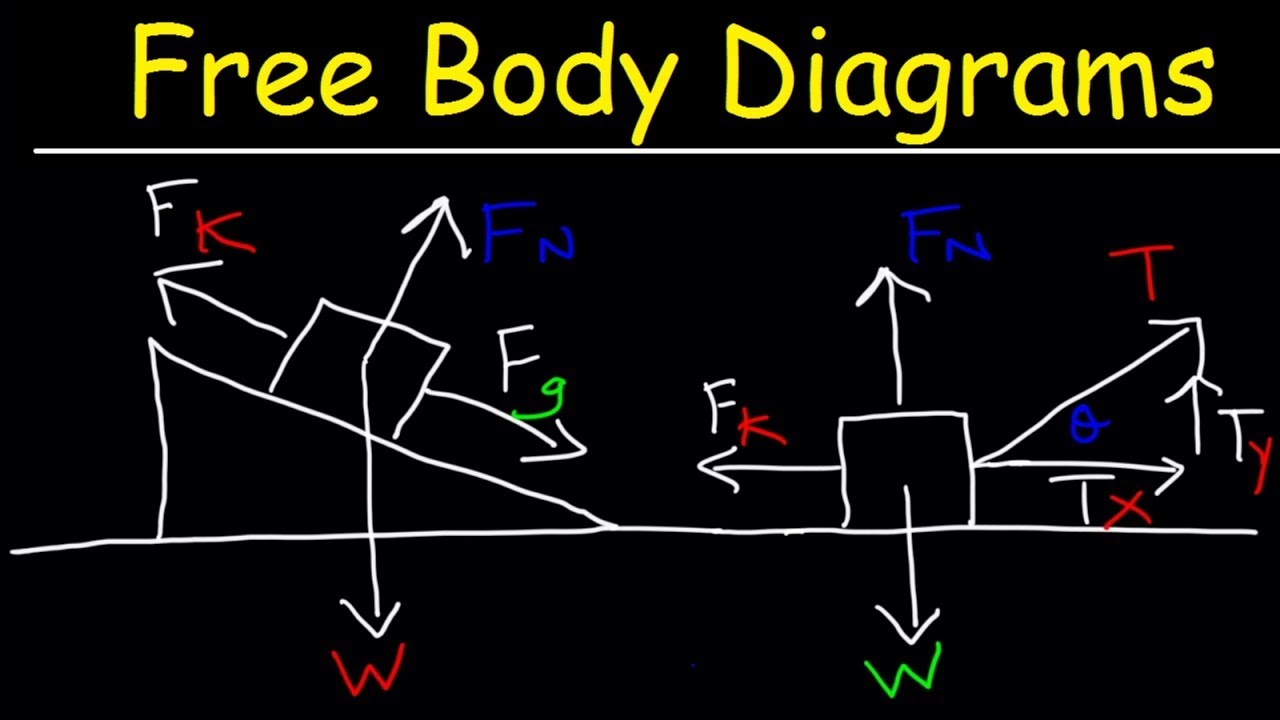
-A free body diagram is a tool used to analyze physical situations by illustrating all the forces acting on a single object and the object itself, which may be represented as a box or a dot.
How is the coordinate system established in a free body diagram?
-The coordinate system is established by choosing the correct direction of the object's motion as one of the positive axes. If the object is not moving, a coordinate axis is chosen based on the context of the problem, such as the direction of the ramp.
What are the three main forces acting on an object at rest on an incline?
-The three main forces are the force of gravity (mg), the normal force (FN) perpendicular to the ramp, and the force of friction (f) acting up the ramp.
What is a pseudo free body diagram and when is it used?
-A pseudo free body diagram is a separate diagram used when the forces do not line up with the coordinate axes. It involves breaking forces into components that align with the axes, simplifying the analysis of the situation.
How are the components of the force of gravity (mg) calculated in a pseudo free body diagram?
-The components are calculated using trigonometry. The parallel component (mg_parallel) is mg * sine(theta), and the perpendicular component (mg_perpendicular) is mg * cosine(theta), where theta is the angle of the incline.
What is Newton's second law and how is it applied to problems involving objects on ramps?
-Newton's second law states that the net force on an object is equal to the mass of the object multiplied by its acceleration (F = ma). It is applied by analyzing the components of forces on the pseudo free body diagram and setting up equations for the net force in each direction, solving for the unknown forces or accelerations.
What is static equilibrium and why is it important in analyzing objects on inclines?
-Static equilibrium occurs when an object is either at rest or moving at a constant velocity, meaning its acceleration is zero. It is important because it indicates that the net force acting on the object is also zero, allowing for the application of balance conditions to solve for unknown forces.
In the example with a 5 kg mass on a frictionless 30-degree incline, how is the force F determined?
-Since the box is in static equilibrium, the net force in the x-direction must be zero. Therefore, force F equals the component of the weight acting down the slope, which is mg * sine(theta). Substituting the given values calculates F to be approximately 24.5 Newtons.
How do you find the component of an object's weight parallel to the hill in a given scenario?
-The component of the object's weight parallel to the hill is found by multiplying the weight of the object (mg) by the sine of the incline angle (theta). This is represented by the formula mg * sine(theta).
In a situation with a block on a ramp with a force F and friction acting on it at constant velocity, how do you determine the magnitude of force F?
-Since the block is moving at constant velocity, it is in static equilibrium, meaning the net force is zero. By applying Newton's second law and setting up an equation for the net force in the x-direction, the magnitude of force F can be determined by balancing the forces acting on the block.
Outlines
📚 Introduction to Analyzing Ramp Scenarios
This paragraph introduces the topic of analyzing physical situations involving objects at rest on inclined planes or ramps. It emphasizes the importance of understanding the forces at play, such as friction, normal force, and weight. The speaker outlines the objectives, which include drawing and labeling a free body diagram, creating a pseudo free body diagram, and using Newton's laws of motion to solve problems related to objects on ramps. The paragraph highlights the interconnected nature of these concepts and encourages reviewing previous lectures for a solid foundation.
🎨 Drawing Free Body Diagrams and Pseudo Free Body Diagrams
In this paragraph, the focus shifts to the practical aspect of drawing free body diagrams and pseudo free body diagrams. The speaker explains the process of representing forces and the object of interest, either as a dot or a box, and labeling all external forces acting on the object. The paragraph delves into the specifics of breaking down forces into components that align with coordinate axes, using trigonometry to determine these components. The speaker provides an example of a box on a ramp and demonstrates how to identify and break down the forces of gravity into parallel and perpendicular components, simplifying the analysis of the situation.
🔍 Applying Newton's Second Law in Ramp Scenarios
This paragraph discusses the application of Newton's second law to analyze objects on inclined planes. The speaker explains how to use the pseudo free body diagram to apply this law in both the x and y directions. The process involves identifying the net force along each axis and setting it equal to the mass times the acceleration, which is zero in cases of static equilibrium. The speaker provides examples of how to calculate the normal force and the force of friction, using the components of the gravitational force and the angle of the ramp. The paragraph emphasizes the systematic approach of using the pseudo free body diagram to derive equations for problem-solving.
📊 Solving Problems with Sample Scenarios
The speaker presents sample problems to illustrate the application of the concepts discussed earlier. These problems involve determining the net force, calculating the normal force, and finding the magnitude of an applied force when a box is at rest on an inclined plane. The paragraph details the steps of identifying forces, drawing free body diagrams, and using trigonometry to find force components along the axes. The speaker shows how to apply Newton's second law to find the magnitude of an unknown force, such as the force holding a box in place on a frictionless ramp. The paragraph reinforces the importance of a methodical approach to problem-solving in physics.
🚀 Final Thoughts on Ramp Analysis
In the concluding paragraph, the speaker reiterates the importance of drawing forces on the object, creating a free body diagram, and using a pseudo free body diagram to simplify the problem. The speaker encourages the application of Newton's second law in both the x and y directions to find the net force and solve for unknowns. The paragraph ends with a reminder to take time and approach each problem systematically, ensuring a clear understanding of the forces at play and the principles of physics involved.
Mindmap
Keywords
💡Free Body Diagram
💡Pseudo Free Body Diagram
💡Newton's Laws of Motion
💡Static Equilibrium
💡Force Components
💡Friction
💡Normal Force
💡Trigonometry
💡Acceleration
💡Coordinate Axes
💡Force Analysis
Highlights
The lecture focuses on analyzing situations involving objects on ramps or inclines, using free body diagrams and Newton's laws of motion.
Free body diagrams are essential tools for analyzing physical situations, showing all forces acting on a single object.
When an object is at rest on an incline, it is subject to the force of gravity, normal force, and frictional force.
The force of gravity acting on an object can be decomposed into components parallel and perpendicular to the incline using trigonometry.
The component of the object's weight parallel to the ramp is given by mg sine-theta, and the perpendicular component by mg cos-theta.
Newton's second law can be applied in both the x and y directions to solve for unknown forces acting on an object on an incline.
In static equilibrium, where an object is at rest, the net force acting on the object is zero, and the acceleration is also zero.
For an object held at rest on a frictionless incline, the force acting up the incline must equal the component of the object's weight parallel to the incline.
In a sample problem, the magnitude of the force holding a 5 kg mass at rest on a 30-degree frictionless incline is calculated using the component of weight.
The lecture demonstrates the systematic approach of identifying forces, drawing free body diagrams, creating pseudo free body diagrams, and applying Newton's laws to find solutions.
A block on an inclined plane with a force acting on it and friction opposing it illustrates the need to calculate the magnitude of the force to maintain constant velocity.
The net force in the x-direction for an object moving at constant velocity on an incline is zero, as the forces acting in the positive direction are balanced by those in the negative.
The magnitude of the force required to maintain constant velocity is found by balancing the frictional force and the component of weight parallel to the incline.
The lecture emphasizes the importance of drawing accurate free body diagrams and pseudo free body diagrams for problem-solving in physics.
The method of applying Newton's second law to find the force acting on an object in equilibrium on an incline is demonstrated through various examples.
The lecture provides a comprehensive guide to analyzing and solving problems involving objects on inclined planes, showcasing the practical application of physical principles.
Transcripts
Browse More Related Video
Free Body Diagrams - Tension, Friction, Inclined Planes, & Net Force

High School Physics - Free Body Diagrams

Free body diagrams: Grade 11 and 12 Physics

2022 Live Review 2 | AP Physics 1 | Understanding Forces and Newton’s Laws

Blocks Sliding Down Ramps, and All That: Physics Help Room
Free-Body Diagrams
5.0 / 5 (0 votes)
Thanks for rating: