MANY ARE STRUGGLING ON THIS WORD PROBLEM

The Math & Geometry Tutor
10 Mar 202406:13
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the presenter simplifies a common word problem involving combined work rates. The scenario presents Eric, who can paint a house in 10 hours, and Aric, who takes 15 hours for the same task. The challenge is to determine how long it would take if both worked together. By establishing that the total work is equivalent to 'one' and using the formula 1/Eric's time + 1/Aric's time = 1/X (where X is the time it takes for both to complete the task together), the video guides viewers to find the least common denominator to solve the fraction problem. The solution reveals that it would take 6 hours for both to paint the house together, emphasizing the importance of understanding the concept of total complete work as 'one' and the effectiveness of the presented formula.

Takeaways
  • 🎨 The problem involves two people, Eric and Aric, painting a house together.
  • ⏰ Eric can paint the house in 10 hours, while Aric takes 15 hours to do the same job.
  • 🤔 The challenge is to find out how long it will take them to paint the house if they work together.
  • 📝 The total work to be done is considered as '1' (one job).
  • 👥 Eric's work rate is 1/10 of the job per hour, and Aric's work rate is 1/15 of the job per hour.
  • 🔢 To solve the problem, we combine their work rates: (1/10) + (1/15)
  • 📈 We find a common denominator, which in this case is 30, to combine the fractions properly.
  • 🧩 After combining, we get the equation: (3/30) + (2/30) = 1/X
  • 📌 By cross-multiplying, we solve for X: 5 * X = 30
  • 🔍 Simplifying the equation, we find that X = 6 hours.
  • 📝 The key formula to remember is: 1/Eric's rate + 1/Aric's rate = 1/Together's rate
  • 🎓 Memorizing this formula allows for easy solving of similar work problems.
Q & A

  • How long does it take for Eric to paint the house alone?

    -It takes Eric 10 hours to paint the house alone.

  • How long does it take for AR to paint the same house alone?

    -AR takes 15 hours to paint the house alone.

  • What is the total complete work considered as in this problem?

    -The total complete work is considered as one in this problem.

  • What is the formula to find the time it takes when two people work together?

    -The formula is 1/Eric's time + 1/AR's time = 1/Together's time (X).

  • How do you find the common denominator for the fractions in this problem?

    -The common denominator is found by identifying the smallest number that is a factor for both 10 and 15, which is 30 in this case.

  • What is the combined fraction representing the work done by Eric and AR together?

    -The combined fraction is (3/30) + (2/30) = 5/30 or 1/6.

  • What is the method used to solve for X in this problem?

    -Cross-multiplication is used to solve for X, by multiplying both sides by the common denominator (30) to isolate X.

  • What is the final answer for how long it takes Eric and AR to paint the house together?

    -If Eric and AR work together, it will take them 6 hours to complete the painting of the house.

  • Why is it important to remember that the total complete work is one?

    -It is important because it simplifies the problem and allows you to apply the formula for solving work problems involving rates.

  • How does the script emphasize the ease of solving such problems?

    -The script emphasizes that these problems are very easy if you follow the taught method and remember the formula.

  • What is the key takeaway from the script for solving similar word problems?

    -The key takeaway is to memorize the formula for combined work rates and apply it to find the time it takes when two or more people work together on a task.

Outlines
00:00
🖌️ Solving a Word Problem: Eric and Aric's Painting Task

This paragraph introduces a word problem involving Eric and Aric painting a house. Eric can paint the house in 10 hours, while Aric takes 15 hours. The problem asks how long it would take if they both painted the house together. The video explains a method to solve this problem by considering the total work as 'one' and using the formula of combined work rates, which is 1/Eric's time plus 1/Aric's time equals 1/X, where X is the time it takes when working together. The explanation includes setting up the fraction equation and finding the common denominator to solve for X.

05:03
🎉 Solution and Conclusion: Eric and Aric's Combined Work Rate

The paragraph concludes the word problem by solving the fraction equation set up in the previous paragraph. By finding the common denominator and setting up the equation (3/30 + 2/30 = 1/X), the video demonstrates how to cross-multiply and solve for X, resulting in X = 6 hours. The summary emphasizes the importance of understanding the concept of total complete work as 'one' and memorizing the formula for combined work rates to solve similar problems. The video ends with a positive note, encouraging viewers to apply this method to other similar word problems.

Mindmap
Keywords
💡word problem
A word problem is a mathematical problem that is presented in a narrative or story-like format, often involving real-world scenarios. In the video, the word problem involves calculating the time it takes for two individuals to paint a house together. The problem requires understanding the rate at which each person can complete the task individually and then combining those rates to find the time it would take for them to complete the task together.
💡solve
To solve in the context of the video means to find the answer or solution to the mathematical word problem presented. It involves applying mathematical concepts and operations to reach a conclusion or an answer. The process of solving the problem in the video involves setting up an equation based on the rates of work and then performing the necessary calculations to find the time it takes for both individuals to paint the house together.
💡Eric
Eric is one of the characters in the word problem presented in the video. He is described as being able to paint a house in 10 hours. His rate of work is a crucial piece of information used to solve the problem of how long it would take for both Eric and Aric to paint the house together.
💡Aric
Aric is the second character in the word problem who is also involved in painting a house. Unlike Eric, Aric takes 15 hours to complete the same task. His rate of work is essential for determining the combined time it would take for both individuals to paint the house together.
💡rate of work
The rate of work refers to the speed at which a task is completed by an individual or a group. In the context of the video, it is the measure of how much of the house each person can paint in an hour. Understanding and calculating the rate of work for both Eric and Aric is key to solving the word problem.
💡combined rate
The combined rate is the total rate at which two or more individuals work together on a task. In the video, it is calculated by adding the individual rates of Eric and Aric to find out how quickly they can paint the house when working together.
💡total complete work
The term 'total complete work' refers to the entire task or job that needs to be done, which is considered as a unit of 'one' in the context of solving work problems. In the video, the total complete work is painting the entire house, and the goal is to find out how long it takes for both Eric and Aric to complete this 'one' task together.
💡fraction problem
A fraction problem is a mathematical problem that involves operations with fractions, which can include addition, subtraction, multiplication, or division of fractions. In the video, the fraction problem is related to determining the combined rate at which Eric and Aric can paint the house and then using that rate to find the total time to complete the task.
💡common denominator
A common denominator is a number that is the denominator for two or more fractions. It is used to express fractions with different denominators on a common basis, allowing for addition or subtraction. In the video, finding a common denominator is a crucial step in solving the fraction problem, as it enables the addition of Eric and Aric's rates to determine their combined rate.
💡cross multiply
Cross multiplying is a technique used in solving equations, particularly with fractions, to eliminate the denominators and make it easier to solve for the unknown variable. In the video, cross multiplying is used to find the value of the unknown time 'X' that represents how long it would take for Eric and Aric to paint the house together.
💡equation
An equation in mathematics is a statement that asserts the equality of two expressions. In the context of the video, the equation is used to represent the relationship between the rates of work of Eric and Aric and the time it would take for them to paint the house together. Solving the equation yields the answer to the word problem.
💡time
In the context of the video, time refers to the duration it takes for Eric and Aric to complete the task of painting a house. The main objective of the word problem is to calculate this time when both individuals work together.
Highlights

The video presents a fun and easy method to solve a word problem involving combined work rates.

Eric paints a house in 10 hours, while Aric takes 15 hours to paint the same house.

The problem asks how long it would take for both to paint the house together.

The total complete work is considered as one unit in the problem-solving approach.

The formula to solve the problem is 1/Eric's time rate + 1/Aric's time rate = 1/X, where X is the time it takes to paint the house together.

To solve the fraction problem, find a common denominator, which in this case is 30.

The numerators become 3 (from 1/10) and 2 (from 1/15) when the denominators are made to be 30.

The equation becomes 3/30 + 2/30 = 5/30, which simplifies to 1/X = 5/30.

By cross-multiplying, we get 5X = 30, which leads to X = 6 hours.

The method can be applied to solve similar word problems involving combined work rates.

Memorizing the formula 1/Eric's rate + 1/Aric's rate = 1/X is key to solving these problems.

The video emphasizes the importance of understanding the concept of the total complete work as one unit.

The presenter expresses enjoyment in teaching this method and hopes the viewers find it helpful.

The video concludes with a positive note, encouraging viewers to apply the learned method to similar problems.

Transcripts

Browse More Related Video

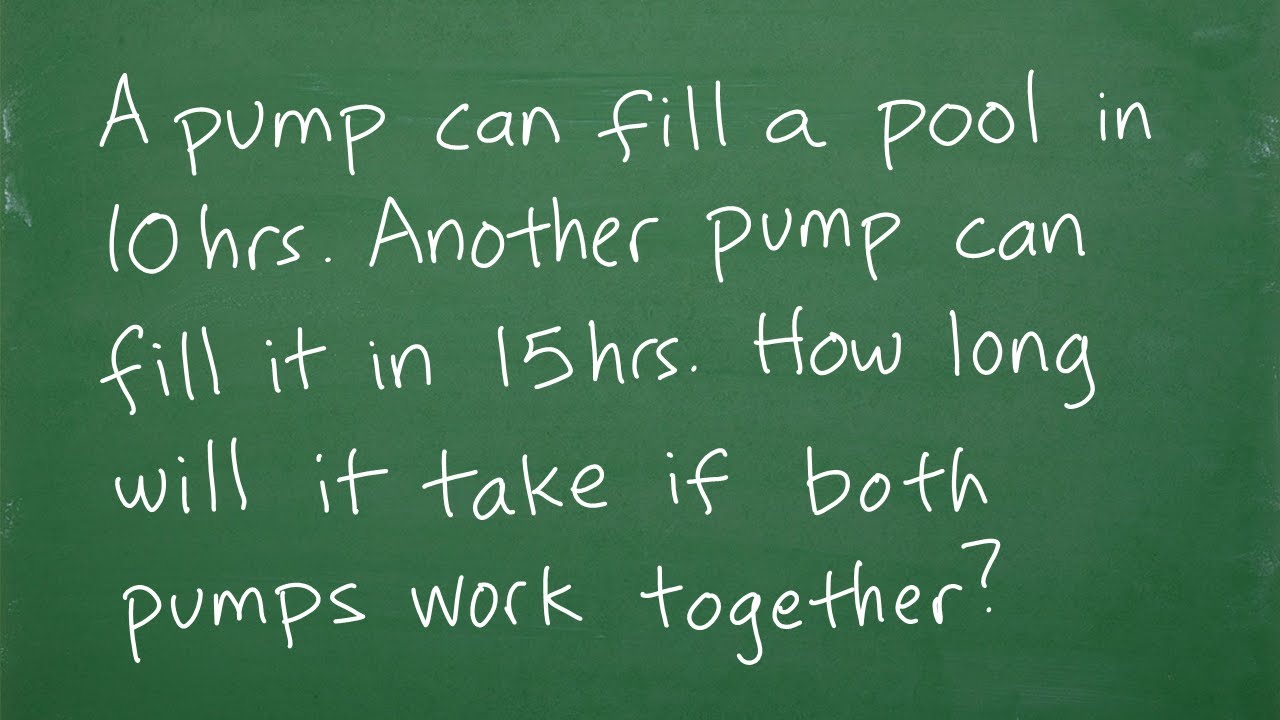
A pump can fill a pool in 10hrs. Another pump can fill it in 15hrs. Both pumps together will take?

Dan can dig a hole in 50min, Jon can do it in 40min, how long will it take if they work together?

Compound Interest & Population Growth Word Problems - Logarithms

An "unsolvable" logic puzzle

Power series of ln(1+x_) | Series | AP Calculus BC | Khan Academy

Exponential Growth and Decay Word Problems & Functions - Algebra & Precalculus

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathSolutionsCollaborativeEffortProblemSolvingTimeManagementEducationalContentFunLearningMathTricksEfficiencyTeamwork