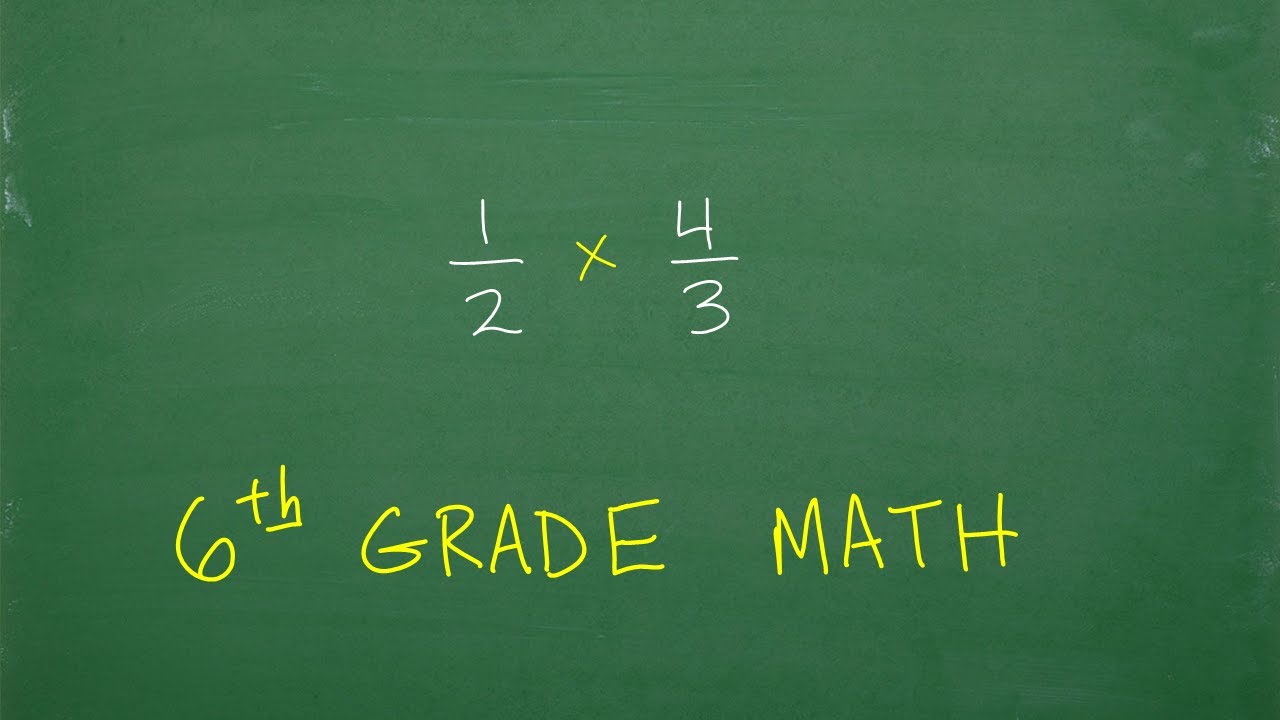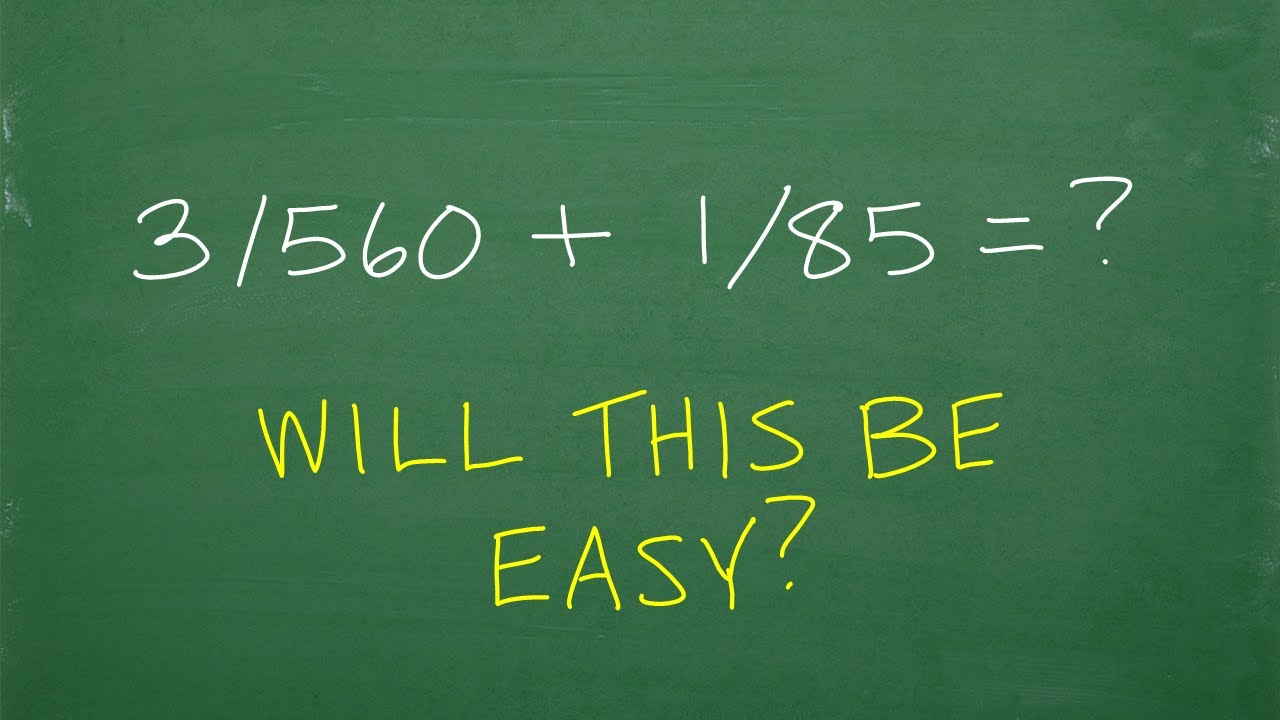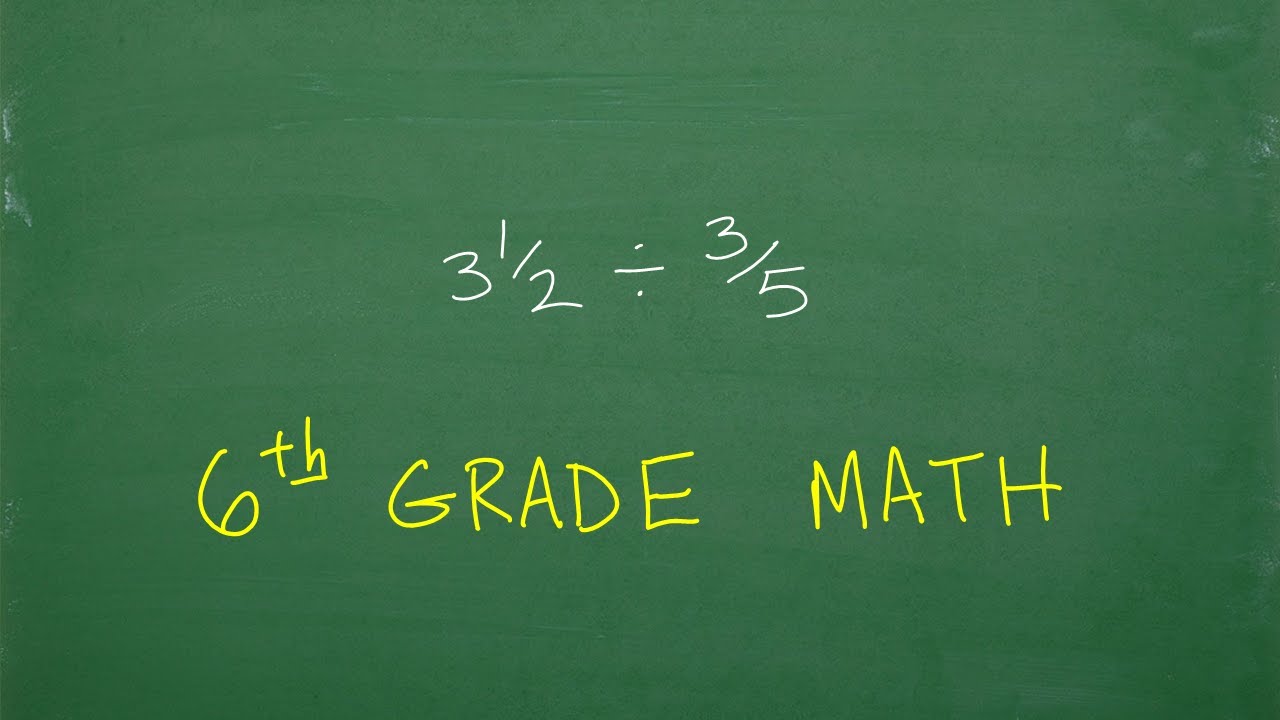(2 and 3/4) plus 1/2 times 5/3 = ? What’s the first thing you should be thinking in this problem?
TLDRIn this instructional video, math teacher John guides viewers through solving a complex fraction problem without a calculator. He emphasizes the importance of understanding the order of operations (PEMDAS) and mastering fraction manipulation techniques. John demonstrates how to multiply fractions, convert mixed numbers to improper fractions, find a common denominator, and add fractions. He also shares tips on avoiding common mistakes, such as unnecessary conversion to mixed numbers, and introduces the 'bow tie' method as a shortcut for adding fractions. The video aims to build confidence in viewers' mathematical abilities and encourages them to practice and master these foundational skills.
Takeaways
- 📝 The problem involves performing operations with fractions, specifically adding 2 and 3/4 to the result of multiplying 1/2 by 5/3 without a calculator.
- 👨🏫 Instructor John emphasizes the importance of focus and careful calculation to avoid errors in fraction problems.
- 🧠 The human brain's ability to compute mathematical problems without a calculator is highlighted as a valuable skill.
- 🔢 The correct answer to the problem is 43/12, which is an improper fraction.
- 📈 Proper fractions have a smaller numerator than the denominator, while improper fractions have a larger numerator.
- 📌 PEMDAS is a mnemonic for remembering the order of operations in mathematics: Parentheses/Brackets, Exponents/Orders, Multiplication-Division (left to right), and Addition-Subtraction (left to right).
- 🤔 The order of operations is crucial in determining the correct result of a mathematical expression.
- 🧩 To add fractions, they must have a common denominator, which is found by identifying the least common multiple of the denominators.
- 🔄 Fractions can be rewritten as equivalent fractions with different denominators by multiplying both the numerator and denominator by the same number.
- 📊 The instructor provides a mini course recommendation for mastering foundational math skills, including fractions.
- 🚫 Avoid unnecessary steps when solving math problems, such as converting an improper fraction to a mixed number if it's not required.
Q & A
What is the main topic of the video?
-The main topic of the video is practicing math skills, specifically working with fractions without the use of a calculator.
What is the problem presented in the video?
-The problem presented is to calculate the result of two and three fourths plus one-half times five thirds.
What is the correct answer to the math problem?
-The correct answer to the math problem is 43 over 12, which is an improper fraction.
What is the significance of the acronym PEMDAS in math?
-PEMDAS stands for Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). It is a mnemonic to help remember the order of operations in math.
How does the video emphasize the importance of order in math operations?
-The video emphasizes that the order in which you perform math operations can significantly affect the result, and following the correct order, such as the one dictated by PEMDAS, is crucial for accurate problem-solving.
What is the first step in solving the given math problem?
-The first step in solving the problem is to identify the correct order of operations, which in this case starts with multiplication, as it takes precedence over addition.
How does the video suggest handling mixed number fractions when adding or subtracting?
-The video suggests converting mixed number fractions to improper fractions before attempting to add or subtract them, especially when dealing with different denominators.
What is the process of finding the lowest common denominator (LCD)?
-To find the LCD, you write the denominators as prime factors, and then include each unique prime factor the greatest number of times it appears in any of the denominators. The product of these prime factors is the LCD.
What is the significance of reducing fractions?
-Reducing fractions simplifies them by dividing both the numerator and the denominator by their greatest common divisor (GCD), making the fraction easier to work with and understand.
What advice does the video give about converting improper fractions to mixed numbers?
-The video advises against unnecessarily converting improper fractions to mixed numbers when the problem can be correctly answered with the improper fraction form, as this can lead to errors and unnecessary work.
What is the bow tie method mentioned in the video, and how is it used?
-The bow tie method is a shortcut technique for adding and subtracting fractions. It involves multiplying the numerators across and the denominators across, then adding or subtracting those products. However, the video notes that this method may not always yield the simplest form of the fraction.
Outlines
📚 Introduction to Fractions and Problem Overview
The video begins with an introduction to working with fractions, emphasizing the importance of focus and avoiding calculators to utilize mental math skills. The problem presented involves calculating the sum of 2 and three-fourths plus one-half times five-thirds. The speaker, John, a math teacher with decades of experience, warns viewers about the potential for errors and encourages them to solve the problem in the comments. He then provides the correct answer, 43 over 12, and explains that this is an improper fraction. John also introduces himself and promotes his math help program, encouraging viewers to like and subscribe for more content.
📝 Understanding the Order of Operations (PEMDAS)
John explains the importance of the order of operations, or PEMDAS, in solving math problems. He describes the acronym PEMDAS, which stands for Parentheses, Exponents (Powers), Multiplication and Division (from left to right), and Addition and Subtraction (from left to right). He clarifies common misunderstandings about the order, particularly the fact that multiplication and division should be performed from left to right, regardless of their order in the expression. John emphasizes the need to apply this order to the given problem, which involves both addition and multiplication.
🧮 Multiplying Fractions and Simplifying
The speaker demonstrates how to multiply fractions, using the example of one-half times five-thirds. He explains that to multiply fractions, you multiply the numerators together and the denominators together. After performing the multiplication, John shows that the result is 5/6. He then transitions to discussing the next step of the problem, which involves adding fractions. John also mentions his Math Foundations course for those needing a refresher on basic math concepts, including fractions.
🔢 Converting Mixed Numbers to Improper Fractions and Finding a Common Denominator
John explains how to convert a mixed number, such as two and three-fourths, into an improper fraction. He shows the process of multiplying the whole number by the denominator and adding the numerator to get the new numerator, resulting in 11/4. He then addresses the need to find a common denominator for the fractions involved in the problem, identifying 12 as the lowest common denominator (LCD). John provides a detailed explanation of how to find the LCD by using prime factorization and emphasizes the importance of using the LCD to add or subtract fractions with different denominators.
🎓 Final Steps: Adding Fractions and Reducing the Result
In the final part of the video script, John demonstrates how to add the fractions once they have been converted to have the common denominator of 12. He shows that 11/4 (converted to 33/12) plus 5/6 (converted to 10/12) equals 43/12. John emphasizes that the final answer should not be unnecessarily converted to a mixed number, as this can lead to errors. He also introduces a shortcut method for adding fractions called the 'bow tie' method, which involves multiplying across the numerators and denominators in a specific order. John concludes by encouraging viewers to practice their math skills and promising more content to help them improve.
Mindmap
Keywords
💡fractions
💡mixed numbers
💡improper fractions
💡order of operations
💡common denominator
💡math foundations
💡divisibility rules
💡simplifying fractions
💡mathematical operators
💡prime factors
Highlights
The importance of focusing and avoiding errors when working with fractions is emphasized.
The problem involves adding two and three fourths to one-half times five thirds without a calculator.
John, the instructor, has decades of experience teaching math and aims to make learning math as easy as possible.
The correct answer to the problem is 43 over 12, which is an improper fraction.
A quick power lesson explains the difference between proper and improper fractions.
The order of operations (PEMDAS) is introduced as a crucial concept for solving the problem correctly.
Multiplication and division should be performed from left to right, regardless of their order in the expression.
The process of multiplying fractions is explained, where you multiply the numerators and denominators respectively.
One-half times five thirds equals five sixths, demonstrated through the multiplication of fractions.
The concept of converting a mixed number to an improper fraction is discussed for easier calculations.
The method of finding the lowest common denominator (LCD) is introduced for adding fractions with different denominators.
The process of converting fractions to have the same denominator using the LCD is demonstrated.
The final step of adding the numerators of fractions with the same denominator is explained.
The importance of not overworking the problem by unnecessarily converting improper fractions to mixed numbers is stressed.
A shortcut method for adding fractions, known as the bow tie method, is briefly introduced.
The video aims to inspire confidence in viewers to improve their math skills and provides resources for further learning.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: