AP Physics Workbook 3.J Centripetal vs Linear Acceleration
TLDRThe video script discusses two scenarios involving circular motion and gravitation in physics. In the first case, an object slides down a cone, accelerating due to gravity, resulting in a normal force dependent on the cosine of the angle. In the second, the object moves at a constant speed in a circular path, leading to a larger normal force due to the centripetal acceleration. The script provides detailed explanations and mathematical derivations for the forces involved, emphasizing the role of trigonometric functions in determining the normal force in both scenarios.
Takeaways
- 📚 The script discusses unit three of AP Physics, focusing on circular motion and gravitation, specifically section three J which compares linear acceleration to circular motion.
- 🔄 In scenario one, an object slides down a cone-shaped ramp due to gravitational force, experiencing linear acceleration towards the bottom.
- 🔄 In scenario two, the object is released to travel at a constant speed in a circular path around a dot, experiencing a change in angular velocity and thus angular acceleration towards the center of rotation.
- 📈 The concept of acceleration is central to understanding both scenarios, with the object accelerating down the cone in the first case and having angular acceleration in the second case.
- 🌐 The force of gravity (mg) acts on the object in both cases, but its effect differs based on whether the motion is linear or circular.
- 📊 The normal force experienced by the object is a result of the gravitational force and is dependent on the angle of inclination (theta) in both scenarios.
- 🔢 For the first case, the normal force can be derived using Newton's second law, with the equation FN = mg*cosine(theta) when there's no vertical motion.
- 🔢 In the second case, the normal force is still calculated using the equation FN = mg*cosine(theta), but the context is different due to the circular motion.
- 📌 As the angle theta approaches 90 degrees, the cosine of theta decreases, affecting the magnitude of the normal force in both scenarios.
- 🔄 The normal force is greater in the second scenario (circular motion) than in the first scenario (linear motion) due to the cosine of theta being in the denominator, causing an increase as theta decreases.
- 📐 The script emphasizes the importance of understanding both the physics and trigonometry involved in these problems to correctly analyze and compare the normal forces in the two scenarios.
Q & A
What is the main topic of the transcript?
-The main topic of the transcript is the comparison of linear acceleration in a scenario where an object slides down a ramp and circular motion where the object travels at a constant speed around a circular path.
What is the significance of the object sliding down the cone in the first case?
-In the first case, the object sliding down the cone represents a scenario of linear acceleration due to the force of gravity. This is equivalent to an object sliding down a ramp, which results in a change in velocity over time.
How does the force of gravity affect the object in both cases?
-In both cases, the force of gravity (mg) acts on the object. In the first case, it causes a linear acceleration as the object slides down, while in the second case, it contributes to the centripetal force necessary for maintaining the object's circular motion.
What is the role of the normal force in the two scenarios?
-The normal force plays a crucial role in both scenarios. In the first case, it balances part of the gravitational force to allow the object to slide down without leaving the surface. In the second case, it provides the necessary centripetal force for the object's circular motion.
What is the relationship between the angle of the cone and the normal force?
-The normal force is dependent on the cosine of the angle (theta) of the cone. As the angle approaches 90 degrees, the cosine value decreases, which in turn affects the magnitude of the normal force in both scenarios.
How does the normal force change as the angle of the cone increases?
-As the angle of the cone increases, the cosine value decreases, leading to a decrease in the normal force in the first case (linear acceleration). Conversely, in the second case (circular motion), the normal force increases because the cosine is in the denominator, and the force normal is inversely proportional to the cosine value.
What is the significance of the angular acceleration in the second case?
-The angular acceleration in the second case is significant because it indicates that the object is not only moving in a circle but also changing its speed (or angular velocity). This change in velocity is directed towards the center of the rotation, which is a result of the object's circular motion.
How does the object's motion in the second case differ from the first case?
-In the second case, the object is in circular motion at a constant speed, which involves a change in direction and thus a change in angular velocity. This is different from the first case, where the object undergoes linear acceleration in a straight line due to gravity.
What is the difference in the normal force between the two cases?
-The normal force is smaller in the first case (linear acceleration) as the angle of the cone increases, due to the decrease in the cosine value. In contrast, the normal force is larger in the second case (circular motion) as the cosine value decreases, because the cosine is in the denominator, leading to a larger force.
What is the mathematical expression derived for the magnitude of the normal force?
-The mathematical expression derived for the magnitude of the normal force is FN = mg * cos(theta). This equation shows that the normal force is directly proportional to the cosine of the angle and the gravitational force acting on the object.
Why is understanding the trigonometric relationship important in this context?
-Understanding the trigonometric relationship is important because it allows us to accurately calculate the normal force and understand how it changes with the angle in both linear and circular motion scenarios. It's crucial for solving problems involving forces on inclined planes and in circular motion.
Outlines
📘 Introduction to Circular Motion and Gravitation
This paragraph introduces the topic of circular motion and gravitation from an AP Physics workbook. It presents two scenarios involving a cone-like object, such as an ice cream cone, with an object either sliding down (case one) or moving in a circular motion at a constant speed (case two). The paragraph discusses the concepts of linear acceleration and angular acceleration, explaining how the force of gravity causes the object to accelerate in case one, and how angular acceleration towards the center of rotation is present in case two due to the object's circular motion. The paragraph also touches on the importance of understanding Newton's second law and the role of force components in these scenarios.
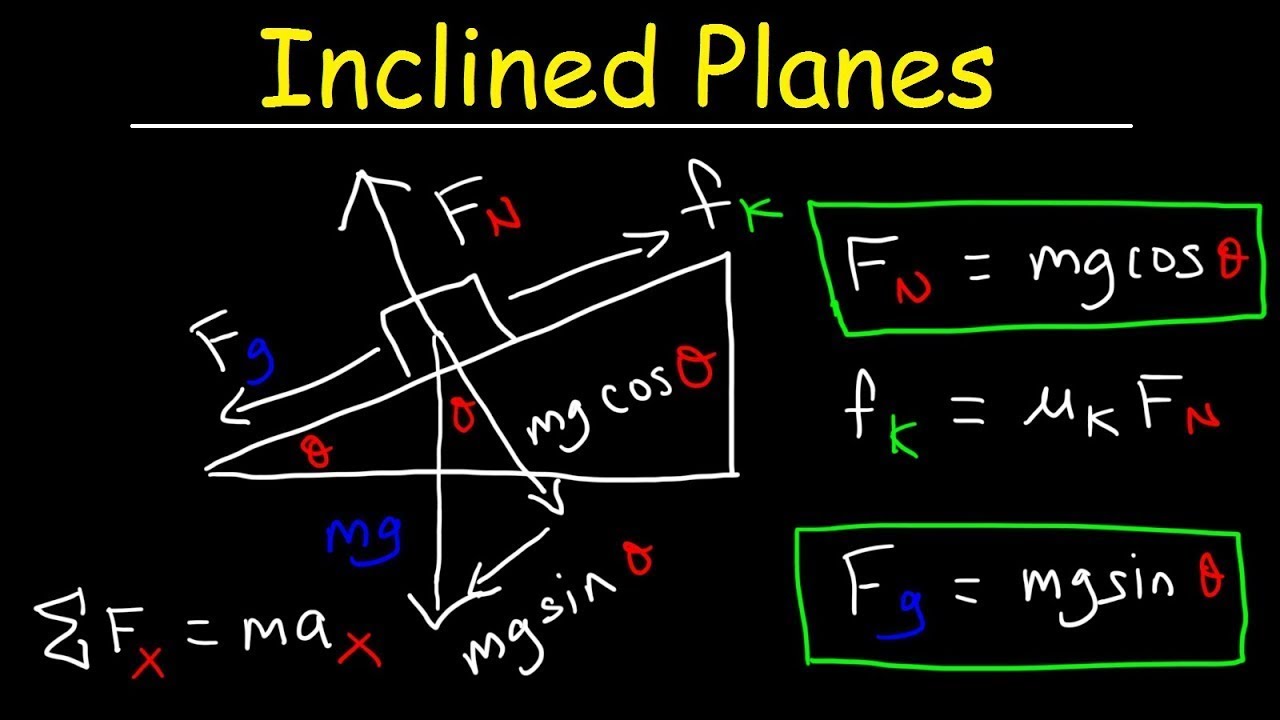
📐 Analysis of Forces in Sliding Motion
This paragraph delves into the analysis of forces acting on an object sliding down a ramp, focusing on the force components. It describes the gravitational force acting on the object and how it can be decomposed into normal and parallel components. The paragraph emphasizes the need to draw accurate diagrams to visualize these forces. It also introduces a problem involving a skier sliding down a ramp, explaining how to label the components of the force and the importance of the normal force in the diagram. The paragraph concludes with an explanation of deriving an expression for the magnitude of the normal force using Newton's second law.
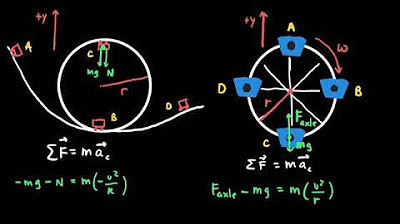
🔄 Centripetal Acceleration and Its Effects
This paragraph discusses the concept of centripetal acceleration in the context of an object revolving around a circular track. It explains how the normal force exerted by the road is perpendicular to the surface and how this force changes when the object is in circular motion. The paragraph clarifies that centripetal acceleration is horizontal and not perpendicular to the slope, which is a key difference from the previous scenario of sliding down a ramp. It also presents an equation for the normal force in the context of circular motion, highlighting the role of cosine theta in determining the magnitude of the normal force.
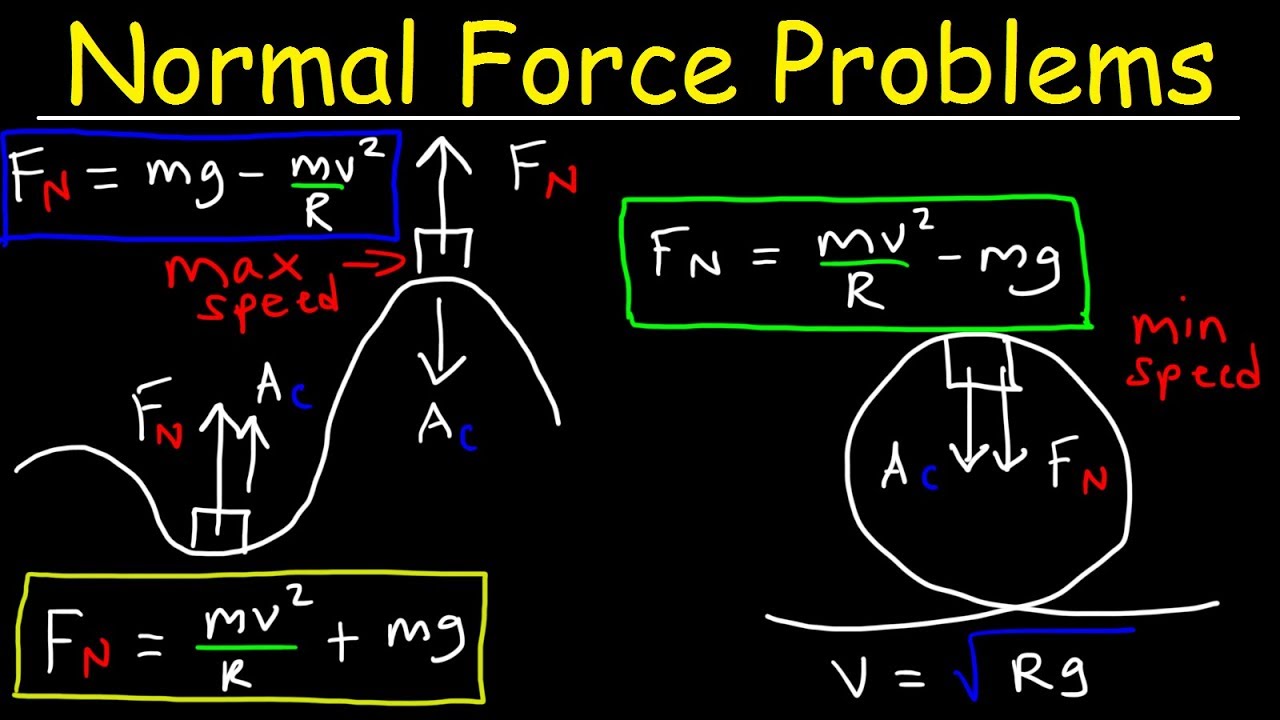
📉 Comparison of Normal Force in Different Scenarios
This paragraph compares the normal force in the two scenarios presented earlier: sliding down a ramp and revolving around a circular track. It uses trigonometric principles to explain how the value of cosine theta affects the normal force in each case. As theta approaches 90 degrees, the cosine value decreases, leading to a smaller normal force in the first scenario (sliding down). Conversely, in the second scenario (circular motion), the decrease in cosine value results in a larger normal force because cosine theta is in the denominator of the equation. The paragraph concludes by emphasizing the importance of understanding these differences to correctly solve physics problems involving circular motion and gravitation.
Mindmap
Keywords
💡Circular Motion
💡Gravitation
💡Acceleration
💡Linear Acceleration
💡Angular Acceleration
💡Normal Force
💡Centripetal Force
💡Trigonometry
💡Newton's Second Law
💡Components of Forces
Highlights
The scenario involves a cone-like structure with an object sliding down towards the bottom.
In the first case, the object slides down from rest, which is equivalent to an object sliding down a ramp, resulting in linear acceleration.
The force of gravity acts on the object, causing it to accelerate down the cone parallel to its surface.
In the second case, the object is released and travels at a constant speed in a circular motion around the cone.
An object in circular motion experiences a change in velocity or angular velocity, leading to angular acceleration.
The angular acceleration is directed towards the center of rotation and is caused by the object's circular motion.
The notes provide a straightforward explanation of labeling the components for case one, involving a skier sliding down a slope.
The force of gravity can be decomposed into two vector components: one in the x-direction (mg sinθ) and one in the y-direction (-mg cosθ).
For the first case, Newton's second law is applied to derive an expression for the magnitude of the normal force.
In the second case, the normal force is perpendicular to the surface of the cone, and its magnitude is determined by the centripetal acceleration.
The normal force is greater in the second case (circular motion) compared to the first case (linear motion) due to the cosine of the angle's role in the equations.
As the angle approaches 90 degrees, the cosine value decreases, affecting the normal force in both cases differently due to its position in the equations.
The cosine of the angle is in the denominator for the second case, causing the normal force to increase as the cosine value decreases.
The explanation demonstrates the relationship between the normal force and the angle of inclination in both linear and circular motion scenarios.
The problem-solving approach involves both algebraic manipulation and trigonometric functions to arrive at the final expressions for the normal force.
The analysis is particularly useful for understanding the physical behavior of objects in different types of motion, such as sliding down a ramp versus moving in a circular path.
The transcript serves as a comprehensive guide for solving physics problems involving circular motion and gravitation, providing both theoretical insights and practical problem-solving steps.
The detailed breakdown of the problem helps in understanding the fundamental principles of physics, emphasizing the importance of accurate calculations and the application of mathematical concepts.
The transcript's content is valuable for AP Physics students, offering a clear and methodical approach to tackle complex problems with confidence.
Transcripts
Browse More Related Video

Dynamics of Uniform Circular Motion

AP Physics Workbook 3.E Maximum speed over the top
Introduction to Inclined Planes
AP Physics 1 Circular Motion and Gravitation Review
Normal Force on a Hill, Centripetal Force, Roller Coaster Problem, Vertical Circular Motion, Physics

College Physics 1: Lecture 22 - Apparent Forces, Orbits, and Gravity
5.0 / 5 (0 votes)
Thanks for rating: