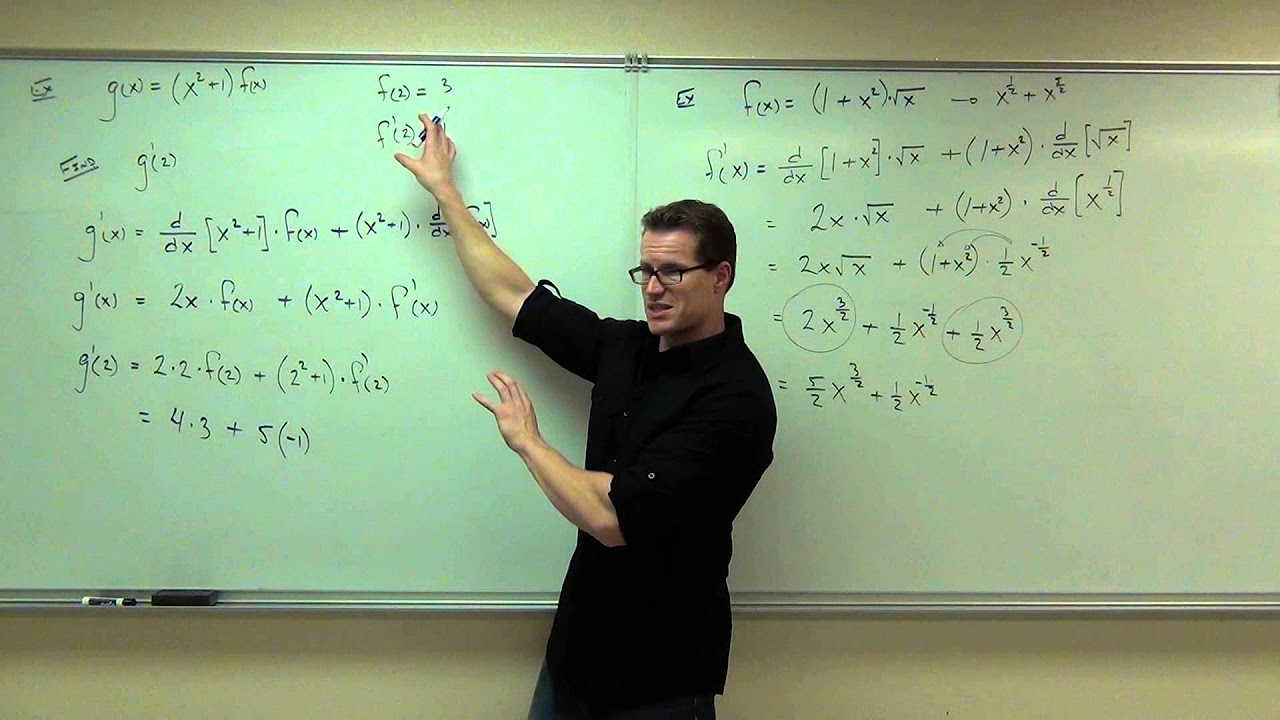How to take Derivatives in Calculus - Differentiation Formulas - [1-3]
TLDRThis transcript delves into the fundamental concepts and formulas of differentiation in calculus. The instructor explains the derivative as the slope of a curve and introduces various rules for calculating derivatives, such as the power rule, product rule, quotient rule, and chain rule. The session emphasizes the importance of understanding these basic principles to solve more complex calculus problems, and encourages practice to master these techniques.
Takeaways
- 📚 The derivative of a function represents the slope of the tangent line to the curve at a specific point, which is essentially the rate of change.
- 🔢 The derivative of a constant is always zero since a constant does not change with respect to the variable.
- 📈 For a function of the form f(x) = c*x^n, the derivative is c*n*x^(n-1), where c is a constant and n is the exponent.
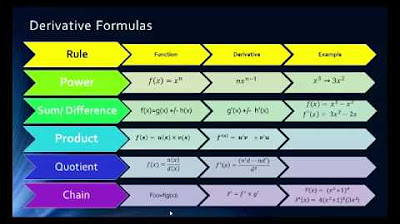
- 🌟 The power rule states that the derivative of x^n is n*x^(n-1), which is used frequently in calculus for polynomial functions.
- 🔥 When adding or subtracting functions, the derivative of the sum or difference is the sum or difference of the derivatives of the individual functions.
- 💡 The product rule for derivatives states that the derivative of a product of two functions is the first function times the derivative of the second plus the second function times the derivative of the first.
- 🌐 For dividing functions, the derivative is more complex and involves the bottom function times the derivative of the top minus the top function times the derivative of the bottom, all over the bottom function squared.
- 📊 When working with radicals and exponents, try to simplify the expression into a form that allows for the application of basic derivative rules.
- 🎯 Always be careful with signs and parentheses when performing derivative calculations to avoid errors.
- 👉 Practice is key in mastering derivative rules and their application to various functions, including polynomials and rational expressions.
Q & A
What is the basic concept of differentiation discussed in the transcript?
-The basic concept of differentiation discussed in the transcript is finding the derivative of a function, which represents the slope of the line tangent to a curve at a specific point. This slope can be thought of as the rate of change of the function with respect to its variable.
How is the derivative of a function denoted in the transcript?
-The derivative of a function is denoted by the prime symbol (') next to the function's name or by using the notation d(f)/dx, which indicates the derivative of the function f with respect to x.
What is the derivative of a constant, according to the rules explained in the transcript?
-The derivative of a constant is zero. This is because a constant does not change with respect to the variable, and thus its slope is zero.
How does the transcript describe the process of taking the derivative of a function that is a constant times another function?
-The transcript explains that the derivative of a function that is a constant times another function can be found by taking the constant out of the function and then taking the derivative of the remaining function. The constant then multiplies the result of this operation.
What is the rule for taking the derivative of a function that is a sum or difference of two other functions?
-The rule for taking the derivative of a function that is a sum or difference of two other functions is to take the derivative of each function separately and then add or subtract the results accordingly.
What is the power rule for differentiation discussed in the transcript?
-The power rule for differentiation discussed in the transcript states that if you have a function of the form x^n, where n is a constant, the derivative of that function is n*x^(n-1).
How does the transcript explain the process of taking the derivative of a product of two functions?
-The transcript explains that to take the derivative of a product of two functions, you multiply the first function by the derivative of the second function and add it to the second function multiplied by the derivative of the first function.
What is the quotient rule for derivatives as described in the transcript?
-The quotient rule for derivatives described in the transcript states that if you have a function that is the quotient of two other functions, the derivative is found by multiplying the derivative of the numerator by the denominator and subtracting the numerator multiplied by the derivative of the denominator, all divided by the denominator squared.
What advice does the speaker give for successfully calculating derivatives?
-The speaker advises taking time, writing down everything with parentheses, keeping signs consistent, not skipping steps, and not trying to do too much in one's head to avoid sign errors, which can lead to incorrect results.
How does the transcript illustrate the application of derivative rules to more complex functions?
-The transcript illustrates the application of derivative rules to more complex functions by walking through examples of functions with various forms, such as sums, products, quotients, and powers, and showing how to apply the rules step by step to find the derivatives.
What is the importance of understanding the derivative properties and rules discussed in the transcript?
-Understanding the derivative properties and rules discussed in the transcript is crucial for being able to take derivatives of various functions, which is at the core of calculus. These rules allow for the analysis of functions' rates of change and slopes at different points, which are fundamental concepts in many areas of mathematics and its applications.
Outlines
📚 Introduction to Differentiation Formulas
This paragraph introduces the concept of differentiation formulas, building upon the previous discussion on the derivative and its significance. The focus is on understanding how to calculate the derivative of a function, which represents the slope of the tangent line to a curve. The explanation emphasizes the importance of the derivative in determining the rate of change and touches on the basic properties of derivatives, such as the derivative of a constant being zero. The paragraph sets the stage for a deeper exploration of calculus through examples and problem-solving.
📈 Power Rule and Derivatives of Monomials
The paragraph delves into the power rule, a fundamental principle in calculus for finding the derivatives of monomials. It explains how to differentiate a function where X is raised to a constant power, n, and highlights the process of bringing the exponent down and adjusting the power accordingly. The explanation is supported by examples, such as differentiating x^2 and x^(-3), to illustrate the application of the power rule. This section is crucial for understanding the derivatives of polynomials and is emphasized as a frequently used method in the course.
🔢 Sum and Difference of Functions' Derivatives
This part of the script discusses the properties of derivatives when dealing with the sum or difference of two functions. It explains that the derivative of a sum (or difference) of functions is equal to the sum (or difference) of their derivatives. The explanation includes a practical example of differentiating a polynomial function, x^2 - 10x + 100, to demonstrate how to apply these properties. The paragraph emphasizes the usefulness of these properties for solving more complex polynomial derivatives.
📊 Derivatives of Products and Quotients
The paragraph introduces the rules for differentiating products and quotients of functions. It explains the product rule, which states that the derivative of a function times another function is the first function times the derivative of the second plus the second function times the derivative of the first. The quotient rule is also discussed, which involves the bottom function times the derivative of the top minus the top function times the derivative of the bottom, all over the bottom function squared. The paragraph provides examples to illustrate these concepts and emphasizes their importance in advanced calculus.
🌐 Solving Complex Derivatives
This section tackles the differentiation of more complex functions, including those involving roots and exponents. The explanation demonstrates how to simplify complex expressions into a form that allows the application of previously learned differentiation rules. Examples given include differentiating a function that includes a fifth root and a squared term, as well as a function with a square root and a term involving division by a squared term. The paragraph emphasizes the importance of practice and careful calculation in mastering these techniques.
🎓 Summary of Derivative Rules
The final paragraph summarizes the key rules and concepts discussed in the video script. It reiterates the importance of understanding the basic definition of a derivative as the slope of the tangent line to a curve at a specific point. The paragraph highlights the core rules for derivatives, including the power rule, sum and difference properties, and the product and quotient rules. The summary serves as a recap of the essential concepts of differentiation, emphasizing their significance in the broader context of calculus.
Mindmap
Keywords
💡Power Rule
Highlights
The class focuses on differentiation formulas and basic calculus concepts.
Derivative is the slope of the line tangent to a curve at a specific point.
The derivative of a function is denoted by a prime symbol or 'df/dx'.
The derivative of a constant is always zero since a constant has no slope.
The derivative of a constant times a function is the constant times the derivative of the function.
The power rule for derivatives states that the derivative of x^n is n*x^(n-1).
The derivative of a sum or difference of functions is the sum or difference of their derivatives.
The derivative of a product of functions requires the use of the product rule.
The derivative of a quotient of functions involves the quotient rule, which is more complex.
When differentiating polynomials, you apply the power rule to each term individually.
The derivative of a function can be found by applying the basic rules of calculus learned in the class.
Understanding the core concepts of derivatives is essential for success in calculus.
The class provides practical examples to illustrate the application of derivative rules.
The power rule is the most commonly used method for taking derivatives.
The class emphasizes the importance of accuracy and attention to detail when working with derivatives.
The rules for derivatives are fundamental for solving more complex calculus problems.
The class introduces methods for differentiating more complex functions, such as those involving roots and exponents.
The process of differentiating functions often involves simplifying them into a form that can be easily worked with.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: