1.4 - Differentiation Using Limits of Difference Quotients
TLDRThe video script delves into the concept of rates of change, transitioning from average rates of change to instantaneous rates at a single point. It introduces the idea of tangent lines, which touch a curve at exactly one point, differing from secant lines that intersect a curve at two points. The script explains how the slope of a tangent line represents the instantaneous rate of change at a specific point on a curve, and how this is calculated using the derivative. The process of finding the derivative involves simplifying the difference quotient and evaluating the limit as 'h' approaches zero. The video also explores the conditions under which a function is not differentiable, such as at discontinuities, sharp corners, or vertical tangent lines. It concludes with a discussion on the importance of derivatives in calculus and hints at future topics on derivative rules for more efficient calculations.
Takeaways
- 📈 The concept of a derivative, or the slope of the tangent line to a curve at a given point, is central to calculus and represents the instantaneous rate of change.
- 🔶 A secant line passes through two points on a curve, while a tangent line touches the curve at a single point, representing the instantaneous change at that point.
- 🔵 The process of finding the derivative involves starting with a difference quotient, simplifying it, and then taking the limit as the interval (h) approaches zero.
- 🚫 At certain points on a function, such as discontinuities, sharp corners, or vertical tangents, the derivative does not exist, and the function is not differentiable at those points.
- 📐 The point-slope form of a line is used to find the equation of the tangent line, requiring both the slope (from the derivative) and a point on the curve.
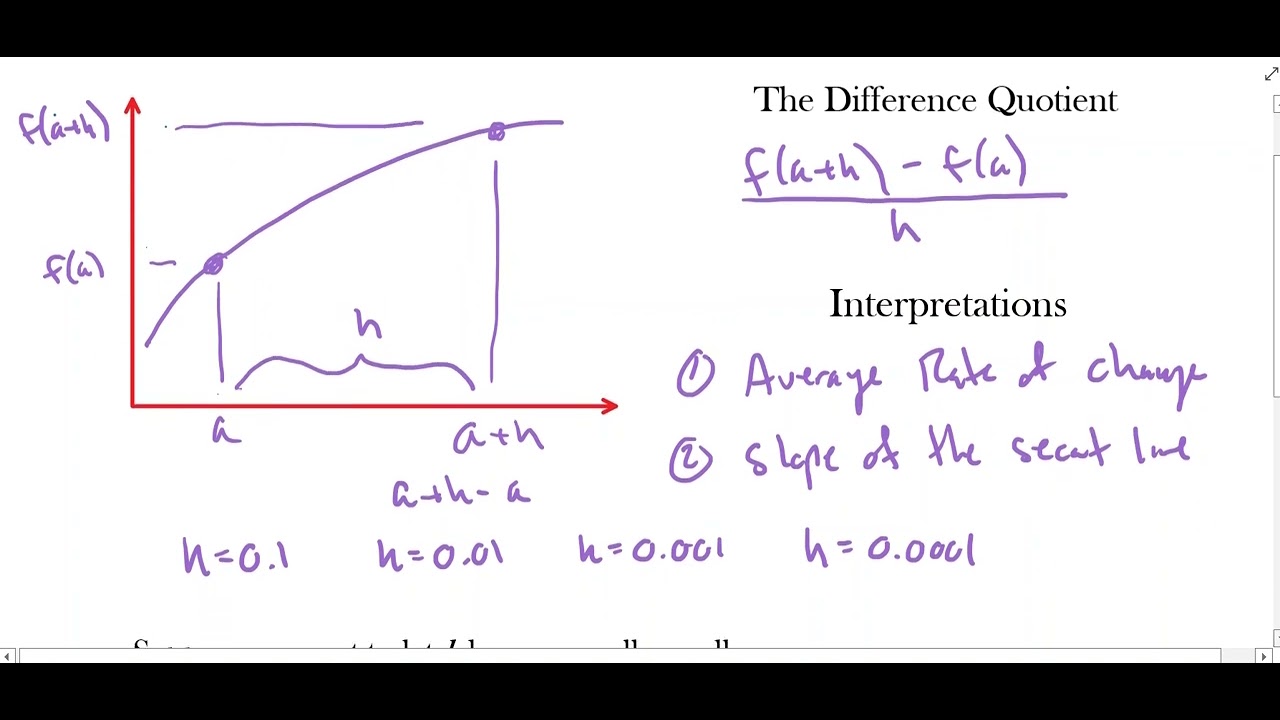
- 🤔 The difference quotient is a key expression for finding the average rate of change between two points, which approximates the slope of the tangent line as the points get infinitely close.
- 📉 For linear functions, the slope of the tangent line is constant and equal to the slope of the function itself, since the tangent line coincides with the graph of the function.
- 🧮 The derivative of a function at a specific point gives the slope of the tangent line at that point, which can be used to find the equation of the tangent line.
- ➗ A common approach to evaluating the limit as h approaches zero is to simplify the difference quotient to cancel out the h in the denominator, avoiding division by zero.
- 🛑 If the limit of the difference quotient as h approaches zero is undefined, it indicates the function is not differentiable at that point, such as at vertical asymptotes or sharp corners.
- ✅ The ability to calculate the derivative exists for most points on a function, provided there are no discontinuities, corners, or vertical tangents at that point.
Q & A
What is the concept of a tangent line in the context of rates of change?
-A tangent line is a line that touches a curve at a single point without crossing it. It represents the instantaneous rate of change at that specific point, as opposed to a secant line, which represents the average rate of change over an interval.
How does the concept of a secant line relate to the average rate of change?
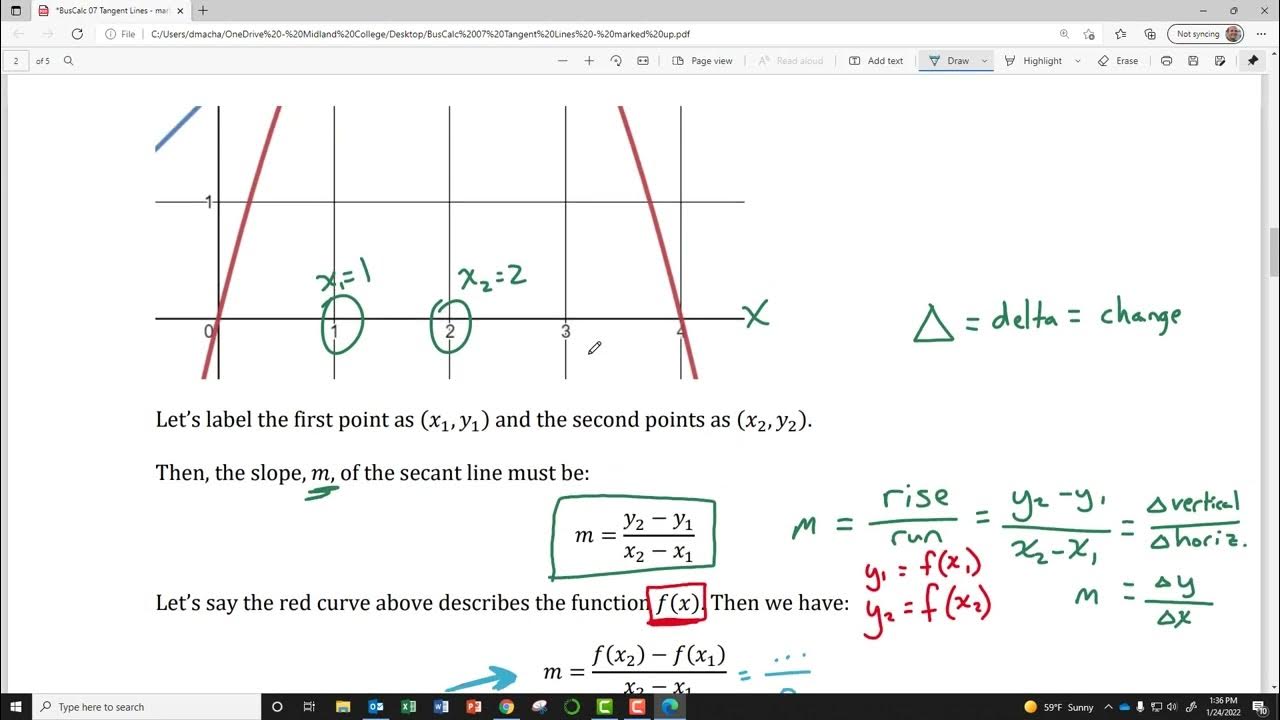
-A secant line connects two points on a curve and represents the average rate of change between those points. It's calculated by finding the difference in y-values over the difference in x-values between the two points.
Why is it necessary to discuss limits when finding the slope of a tangent line?
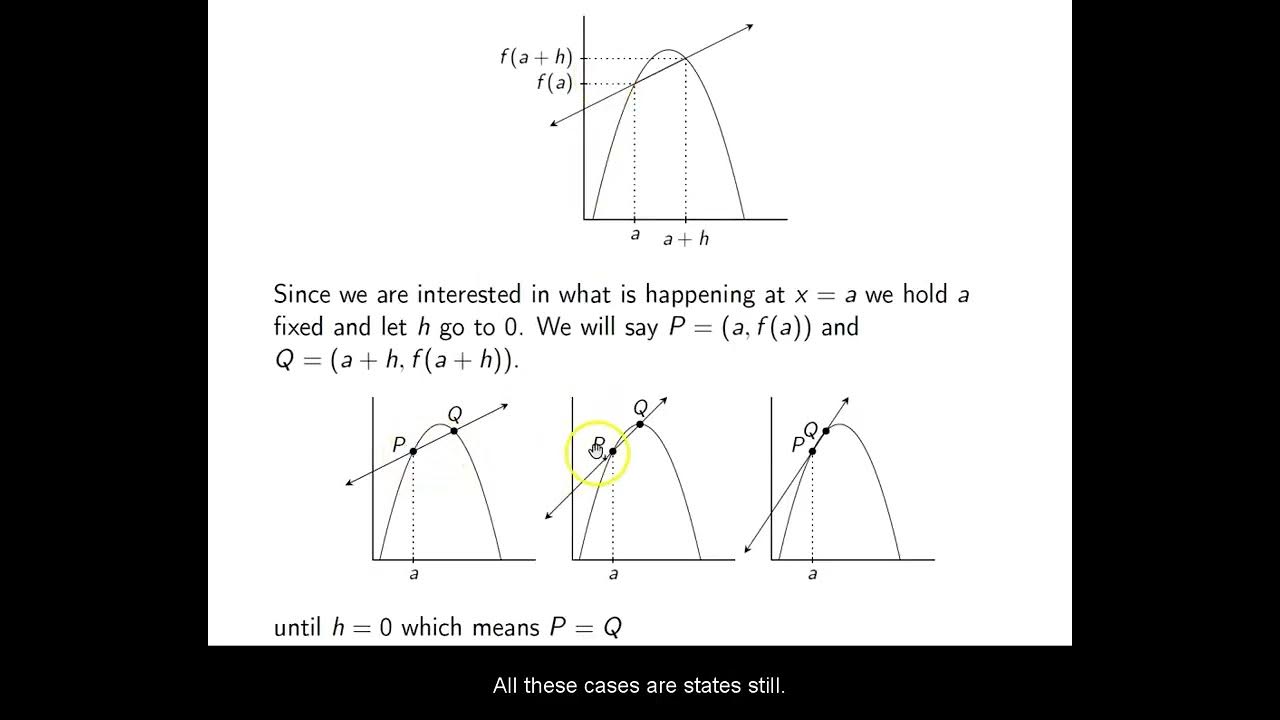
-Limits are necessary because to find the slope of a tangent line, we need to consider what happens as we take an additional point on the curve and move it infinitesimally closer to the point of interest. The concept of a limit allows us to evaluate the behavior of the function as this point approaches the specific point on the curve.
What is the difference quotient formula?
-The difference quotient formula is an expression used to calculate the average rate of change of a function over an interval. It is given by (f(x + h) - f(x)) / h, where f(x) is the function, x is a point on the function, and h is the interval.
How does the slope of the secant line relate to the slope of the tangent line?
-The slope of the secant line approximates the slope of the tangent line as the interval between the two points on the curve becomes smaller. As the interval approaches zero (the two points become infinitesimally close), the slope of the secant line converges to the slope of the tangent line at the point of tangency.
What is the derivative of a function, and how is it related to the slope of the tangent line?
-The derivative of a function at a particular point is the instantaneous rate of change at that point, which is also the slope of the tangent line to the function at that point. It is found by taking the limit of the difference quotient as h approaches zero.
How can you determine if a function is differentiable at a certain point?
-A function is differentiable at a certain point if the limit of the difference quotient exists as h approaches zero. If the limit exists, the function has a derivative at that point, and there is a unique slope for the tangent line.
What are the conditions under which a function is not differentiable?
-A function is not differentiable at a point if there is a discontinuity, a sharp corner, or a vertical tangent line at that point. These conditions prevent the existence of a unique tangent line and, consequently, a well-defined derivative.
What is the point-slope form of a line, and how is it used to find the equation of a tangent line?
-The point-slope form of a line is given by y - y1 = m(x - x1), where m is the slope and (x1, y1) is a point on the line. To find the equation of a tangent line, you use the slope of the tangent line (the derivative of the function at the point) and a point on the curve (the coordinates at which the tangent line touches the curve).
How does the process of finding the derivative of a function relate to the concept of instantaneous change?
-Finding the derivative of a function is directly related to the concept of instantaneous change. The derivative at a point represents the rate of change of the function at that specific instant, which is the same as the slope of the tangent line at that point. It is the limit of the average rate of change as the interval length approaches zero.
What is the role of the difference quotient in finding the derivative of a function?
-The difference quotient is an expression that represents the average rate of change of a function over an interval. By evaluating the limit of the difference quotient as the interval length approaches zero, we find the derivative of the function, which is the instantaneous rate of change at a point.
Outlines
🔍 Introduction to Instantaneous Change and Tangent Lines
The video begins by transitioning from the concept of average rate of change to instantaneous change, focusing on change at a single point rather than over an interval. It introduces the idea of tangent lines, which relate to instantaneous change, as opposed to secant lines which represent average change. The tangent line is described as touching the curve at a single point and being parallel to the curve at that point, symbolizing the instantaneous rate of change. The necessity to discuss the slope of the tangent line and its equation is also highlighted.
📐 Secant Lines and the Generation of Tangent Lines
The paragraph delves into the relationship between secant lines and tangent lines. It explains how a secant line, passing through two points on a curve, can be used to approximate the tangent line by moving the additional point closer to the point of interest (point 'p'). As this point approaches 'p', the secant line more closely resembles the tangent line, allowing for the calculation of the tangent's slope at the specific point.
🎢 The Process of Shrinking 'h' to Define Tangent Lines
This section describes the mathematical process of shrinking the distance 'h' between two points on a curve to define the tangent line. It emphasizes that as 'h' approaches zero, the secant line becomes effectively the same as the tangent line, allowing for the calculation of the instantaneous rate of change. The concept of limits is introduced as a fundamental tool in this process, with the difference quotient being a key formula for these calculations.
🧮 The Derivative as the Instantaneous Rate of Change
The video explains that the derivative of a function at a given point is the instantaneous rate of change at that point, which is found by taking the limit of the difference quotient as 'h' approaches zero. The concept of the derivative is presented as a function itself, denoted by f'(x), and the process of finding the derivative involves simplifying the difference quotient and evaluating the limit as 'h' approaches zero.
📉 Differentiability and the Conditions for a Function to Have a Derivative
The paragraph discusses the conditions under which a function is differentiable, meaning it has a derivative. It outlines that a function is not differentiable at points of discontinuity, sharp corners, or where the tangent line would be vertical (undefined slope). The concept of the derivative representing the slope of the tangent line is used to explain why these conditions prevent differentiability. The importance of differentiability in calculus is emphasized, as it is a fundamental concept in both differential and integral calculus.
📚 Strategies for Calculating Derivatives
The final paragraph of the script hints at future discussions on alternative strategies for calculating derivatives, beyond the direct evaluation and simplification of the difference quotient. It suggests that as functions become more complex, the need for derivative rules arises to make the process more efficient and manageable. These rules will be introduced to facilitate the calculation of derivatives in a more time-saving manner.
Mindmap
Keywords
💡Rates of Change
💡Tangent Lines
💡Secant Lines
💡Instantaneous Change
💡Derivative
💡Difference Quotient
💡Limit
💡Slope
💡Continuous Function
💡Discontinuity
💡Point-Slope Form
Highlights
The concept of instantaneous change is introduced as a shift from average rate of change, focusing on change at a single point rather than over an interval.
Tangent lines are described as touching a curve at a single point, contrasting with secant lines that intersect a curve at two points.
The slope of a tangent line represents the instantaneous rate of change at a specific point on a curve.
The process of finding the slope of a tangent line involves using a secant line that passes through a specific point and a neighboring point, then moving the neighboring point closer to the point of interest.
The difference quotient is a formula used to calculate the slope of a secant line, which can be used to approximate the slope of a tangent line as the points get infinitely close.
The limit of the difference quotient as the distance between two points (h) approaches zero gives the instantaneous rate of change or the slope of the tangent line.
The derivative of a function at a particular point is defined as the limit of the difference quotient as h approaches zero, which is also known as the instantaneous rate of change at that point.
The derivative can be notated as f'(x), where f is the original function and x is the point at which the derivative is taken.
If the limit of the difference quotient exists, the function is considered differentiable at that point.
The process of finding the derivative involves writing the difference quotient, simplifying it, and then evaluating the limit as h approaches zero.
For linear functions, the slope of the tangent line is constant and equal to the slope of the function itself.
For more complex functions, the derivative provides a formula for calculating the slope of the tangent line at any point on the curve.
The point-slope form of a line is used to find the equation of the tangent line at a specific point on a curve.
Functions are not differentiable at points of discontinuity, sharp corners, or where the tangent line is vertical due to an undefined slope.
The concept of differentiability is important for understanding the behavior of a function and its graph, including where it is smooth and where it has unique properties.
Derivative rules will be introduced to simplify the process of finding derivatives for more complex functions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: