AP Calculus AB: Lesson 2.1: The Difference Quotient
TLDRIn this lesson, Michelle Kremmel delves into the concept of the derivative, illustrating it as the limit of the difference quotient. She reviews the average rate of change formula, connects it to the slope of a secant line, and introduces the derivative as the instantaneous rate of change. Kremmel explains the derivative's role in determining the slope of a tangent line to a curve at a specific point and its significance in various mathematical contexts, such as differentiability and units of measure. The lesson also covers the process of finding the derivative using the limit definition and applies it to linear and non-linear functions, highlighting the constant slope in linear functions and varying slopes in curves.
Takeaways
- 📚 The lesson focuses on understanding the difference quotient and its relation to the derivative of a function, which is defined as the limit of the difference quotient.
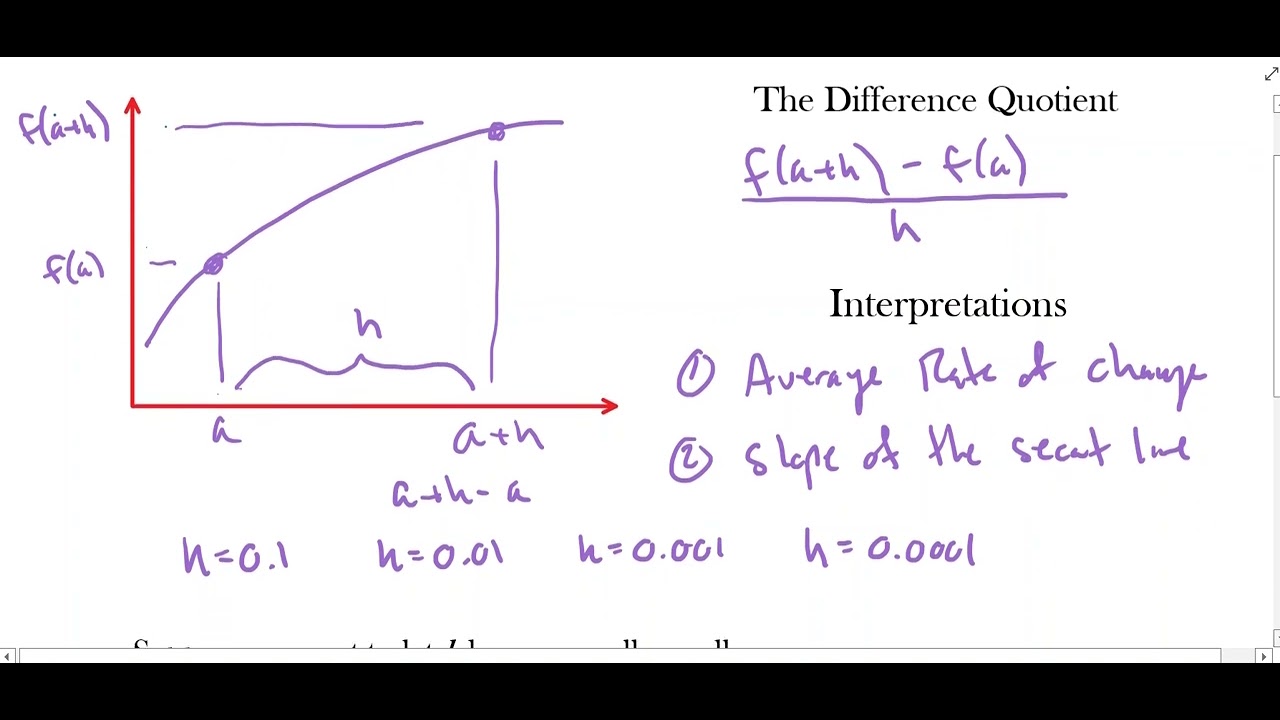
- 📈 The average rate of change formula is reviewed, highlighting its application in calculating the slope of a line segment between two points on a graph.
- 🔍 The concept of the slope of a secant line is introduced, which is the average rate of change between two points and is crucial for understanding the derivative.
- 📉 The derivative, denoted as f'(a), is formally defined as the limit of the difference quotient as h approaches zero, representing the instantaneous rate of change of a function at a specific point.
- 🔑 The term 'differentiable' is explained, indicating that a function is differentiable at a point if its derivative exists at that point.
- 📝 The process of 'differentiation' is introduced as the act of finding the derivative of a function at a given point.
- 📐 The derivative is related to the slope of the tangent line to the function at a specific point, emphasizing its importance in calculus.
- 📈 The units of the derivative are discussed, showing that it represents the rate of change per unit of the independent variable.
- 📉 The difference between average and instantaneous rate of change is clarified, with the derivative representing the instantaneous rate of change.
- 📝 The equation of the tangent line to a function at a point is provided, using the point-slope form of a line equation and highlighting its significance in approximating function values.
Q & A
What is the average rate of change of a function on a closed interval from a to b?
-The average rate of change of a function f on a closed interval from a to b is given by the formula (f(b) - f(a)) / (b - a), which represents the change in the function's value over the interval divided by the change in the x-values over the same interval.
How can the average rate of change be thought of in terms of geometry?
-The average rate of change can be thought of as the slope of a line segment connecting two points on the graph of the function, where the y-coordinates of the points are f(a) and f(b), and the x-coordinates are a and b, respectively.
What is the difference between the average rate of change and the derivative of a function?
-The average rate of change is the ratio of the change in the function's value to the change in the independent variable over an interval, while the derivative is the instantaneous rate of change at a specific point, found by taking the limit of the average rate of change as the interval approaches zero.
What is the definition of the derivative of a function f with respect to x at a point x=a?
-The derivative of a function f with respect to x at a point x=a, denoted as f'(a), is defined as the limit of (f(a+h) - f(a)) / h as h approaches zero, provided this limit exists.
How does the derivative relate to the slope of a curve?
-The derivative of a function at a given point represents the slope of the tangent line to the curve at that point, which is also referred to as the instantaneous rate of change of the function at that point.
What is the point-slope form of the equation of a line, and how is it used in calculus?
-The point-slope form of the equation of a line is y - y1 = m(x - x1), where m is the slope and (x1, y1) is a point on the line. In calculus, it is used to write the equation of the tangent line to a function at a specific point, using the derivative as the slope (m) and the function's value at that point as (x1, y1).
How can the derivative be used to estimate the value of a function at a point close to another point where the function's value and derivative are known?
-The derivative can be used to estimate the value of a function at a nearby point by using the tangent line equation, which is derived from the point-slope form, with the known point and the slope given by the derivative at that point.
What does it mean for a function to be differentiable at a point x=a?
-A function is said to be differentiable at a point x=a if the derivative exists at that point, meaning the limit used to define the derivative does not result in an indeterminate form and exists as a real number.
How does the derivative relate to the units of measure of a function?
-The derivative f'(a) is measured in units of the function's output per unit of the input variable. For example, if the function represents cost in dollars and the input variable is time in seconds, the derivative would be measured in dollars per second.
Can you provide an example of how to compute the derivative of a function using the limit definition?
-Sure. For the function f(x) = x - x^2, to compute the derivative f'(2), you would use the limit definition: f'(2) = lim(h->0) [f(2+h) - f(2)] / h. After substituting and simplifying, you would find that f'(2) = -3.
Outlines
📚 Introduction to Derivatives and Average Rate of Change
In this lesson, Michelle Kremmel introduces the concept of derivatives as the limit of a difference quotient, which is the instantaneous rate of change of a function. The average rate of change is reviewed first, defined as the change in the function's value over an interval divided by the change in the independent variable. This concept is related to the slope of a line and is generalized from the idea of average velocity. The lesson sets the stage for understanding derivatives by using the average rate of change formula and visualizing it on a graph, where the slope of the secant line between two points on the function represents the average rate of change.
🔍 Derivative Definition and Instantaneous Rate of Change
The lesson continues by formally defining the derivative as the limit of the average rate of change as the interval width approaches zero, thus becoming the instantaneous rate of change. This is illustrated with the difference quotient, which is the formula for the derivative. The derivative is denoted as f'(a) and represents the slope of the tangent line to the function at a specific point x=a. The importance of the limit in this definition is emphasized, as it distinguishes the derivative from the average rate of change. The derivative's existence, indicated by the limit, is also discussed, noting that it may not always exist at certain points.
📈 Derivative as Slope and Differentiability
This section delves deeper into the derivative's interpretation as the slope of the curve or the tangent line at a point. The concept of differentiability is introduced, stating that if the derivative exists at x=a, the function is differentiable at that point. The derivative's role in determining the instantaneous rate of change is reiterated, and the difference between average and instantaneous rates of change is highlighted. The vocabulary of differentiation is also introduced, including terms like 'differentiable,' 'differentiate,' and 'differentiation.'
📐 Units of Measure and the Slope of the Tangent Line
The lesson explains that the derivative, or the instantaneous rate of change, has units of the dependent variable per unit of the independent variable. This is illustrated with an example where the cost function is measured in dollars and the quantity in bracelets, resulting in the derivative being measured in dollars per bracelet. The derivative's geometric interpretation as the slope of the tangent line to the curve at a point is also discussed, emphasizing the difference between the constant slope of a line and the varying slope of a curve.
📘 Equation of the Tangent Line and Its Importance
The point-slope form of the equation of a line is introduced as the method for writing the equation of the tangent line to a function at a specific point. The importance of memorizing this equation is stressed, as it is central to calculus. The relationship between the derivative, the slope of the tangent line, and the curve's slope at a point is reiterated. The lesson also poses potential questions that might be asked regarding the tangent line, such as finding the slope of the tangent line at a specific x-value or approximating function values using tangent lines.
📉 Visualizing the Derivative with Graphs
The script uses a series of graphs to visually demonstrate the concept of the derivative. As the interval width (h) approaches zero, the secant lines between points on the function become closer and closer to the tangent line at a point, illustrating the transition from the average rate of change to the instantaneous rate of change. The importance of the limit in the definition of the derivative is emphasized through this visual progression.
📝 Calculating Derivatives Using the Difference Quotient
An example is provided to demonstrate the calculation of the derivative using the difference quotient. The function f(x) = x - x^2 is used to find the derivative at x=2. The process involves algebraic manipulation to simplify the expression and then taking the limit as h approaches zero, resulting in the derivative value. The significance of the limit in obtaining the instantaneous rate of change is highlighted.
🔢 Linear Functions and Constant Slope
The properties of linear functions are discussed, emphasizing that the slope is constant across the entire function. This is contrasted with the varying slope of a curve at different points. The average rate of change for a linear function is shown to be constant, regardless of the interval chosen, and the derivative of a linear function is computed to demonstrate that it is constant, as expected.
🎈 Application of Derivatives in Real-World Problems
The derivative is applied to a real-world problem involving the volume of a balloon changing as it is filled with air. The volume function V(r) = (4/3)πr^3 is given, and the average rate of change of volume with respect to the radius is calculated for different intervals. The derivative is used to find the instantaneous rate of change at specific points, highlighting the application of derivatives in understanding how quantities change in real situations.
📉 Estimating Function Values Using Tangent Lines
The lesson concludes with an example of estimating the value of a function at a point using the tangent line. Given a function with a known value and derivative at x=2, the tangent line equation is used to estimate the function value at x=2.5. This demonstrates the practical use of derivatives in approximating function values and understanding the local behavior of functions.
Mindmap
Keywords
💡Derivative
💡Difference Quotient
💡Average Rate of Change
💡Limit
💡Instantaneous Rate of Change
💡Slope
💡Tangent Line
💡Linear Function
💡Differentiable
💡Units of Measure
Highlights
Introduction to the concept of the difference quotient.
Review of the formula for the average rate of change: f(b) - f(a) / (b - a).
Explanation of average rate of change as a slope calculation.
Generalization of the average rate of change formula to the interval [a, a + h].
Visual representation of points a and a + h on a graph.
Construction and labeling of a right triangle to calculate slopes.
Identification of the slope of the secant line as f(a + h) - f(a) / h.
Definition of the derivative of a function at x = a using limits.
Explanation of instantaneous rate of change as the limit of the average rate of change.
Introduction to the concept of differentiability.
Explanation of the relationship between differentiability and the existence of derivatives.
Explanation of the difference between average rate of change and instantaneous rate of change.
Use of the limit definition of the derivative to compute derivatives at specific points.
Graphical representation and interpretation of the derivative as the slope of the tangent line.
Application of the tangent line equation to find approximate values of a function at specific points.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: