AP Calculus AB: Lesson 6.2 Part 2 (Limit Definition of Definite Integral)

Michelle Krummel

22 Feb 202140:04

EducationalLearning

32 Likes 10 Comments

TLDRIn this lesson, Michelle Krummel explores the concept of the limiting value of the Riemann sum, which serves as the foundation for defining the definite integral. She explains the notation and process of breaking an interval into sub-intervals, calculating the width and height of rectangles under a curve, and summing these areas to approximate the area under the curve. Michelle then demonstrates how to use the Riemann sum to find the exact area under the curve as the number of rectangles approaches infinity, transitioning from summation to integral notation. She also covers properties of summation and applies them to evaluate definite integrals, providing step-by-step examples and suggesting the use of a graphing calculator for verification.

Takeaways

📚 The lesson focuses on the concept of the limiting value of the Riemann sum and its use in defining the definite integral.
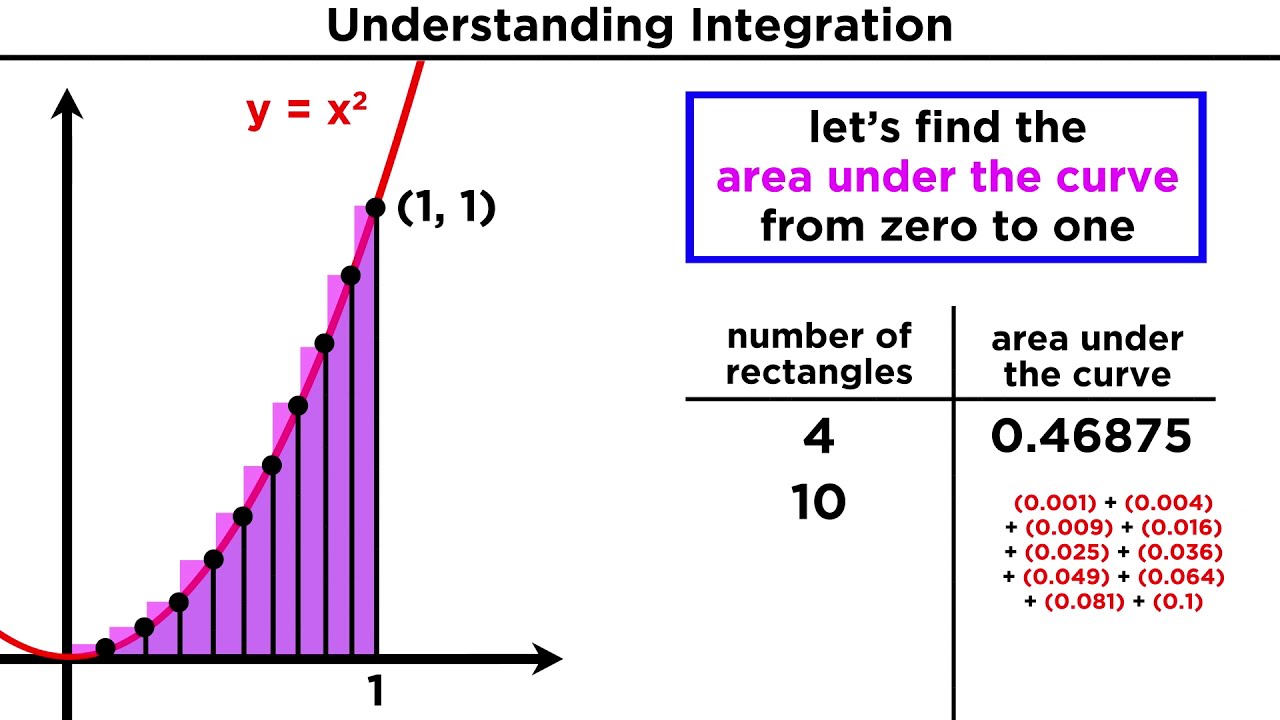
📈 The Riemann sum is introduced as a method to approximate the area under a curve by summing rectangles, which becomes the definite integral as the number of rectangles approaches infinity.
🔢 Notation is discussed for the number of rectangles (n), the width of each rectangle (Δx), and the height (f(x_sub_k)) in the context of the Riemann sum.
📐 The width of each rectangle is uniform and can be expressed as Δx or (b - a) / n, where a and b are the interval endpoints.
📉 The height of each rectangle varies and is determined by the function value at the right endpoint of each sub-interval, f(x_sub_k).
📝 An expression for the area of each rectangle is given as the product of its width (Δx) and height (f(x_sub_k)).
🌟 The total area under the curve is represented by the summation (sigma notation) of the areas of all rectangles, which simplifies to the integral notation as n approaches infinity.
🔍 The properties of summation are explored, including how constants and constant multiples are handled within summations, and the ability to split summations into multiple parts.
📉 The summation formulas for the sum of the first n natural numbers, the sum of the squares of the first n natural numbers, and the sum of the cubes are provided and used to evaluate definite integrals.
📝 Examples are worked through to demonstrate the translation from integral notation to Riemann sum notation and the application of summation properties to evaluate definite integrals.
🛠 The use of a graphing calculator to verify the results of definite integrals is suggested, highlighting the practical application of the theoretical concepts discussed.

Q & A

What is the main topic of the lesson presented by Michelle Krummel?
-The main topic of the lesson is the limiting value of the Riemann sum and its use in defining the definite integral.
What is the purpose of breaking the interval from 'a' to 'b' into sub-intervals?
-The purpose of breaking the interval into sub-intervals is to approximate the area under the curve of a function using rectangles, which is part of the process of calculating the definite integral.
How is the width of each rectangle in a Riemann sum expressed?
-The width of each rectangle is expressed as 'delta x', which is the same for all rectangles when the intervals are of equal width.
What is the expression for the height of the k-th rectangle in a Riemann sum?
-The height of the k-th rectangle is given by the function evaluated at the right endpoint of the sub-interval, which is f(x_sub_k).
How is the area of each rectangle in a Riemann sum calculated?
-The area of each rectangle is calculated by multiplying the width of the sub-interval (delta x) by the height of the rectangle (f(x_sub_k)).
What is the sigma notation used for in the context of Riemann sums?
-The sigma notation is used to represent the summation of the areas of all the rectangles in the Riemann sum.
What is the significance of taking the limit as n approaches infinity in the Riemann sum?
-Taking the limit as n approaches infinity allows the width of each sub-interval to approach zero, which minimizes the error in the Riemann sum and leads to the exact area under the curve.
What does the integral symbol ∫ represent in calculus?
-The integral symbol ∫ represents the definite integral, which is the limit of the Riemann sum as the number of rectangles approaches infinity.
How is the definite integral notation connected to the Riemann sum notation?
-The definite integral notation is a simplified form of the Riemann sum notation, where the summation symbol, the limits of integration, and the function are combined to represent the exact area under the curve.
What are some properties of summation that are discussed in the script?
-Some properties of summation discussed include summing a constant (c times n), factoring out a constant multiple, and splitting a single summation into multiple summations.
How are summation formulas used to evaluate definite integrals?
-Summation formulas, such as the sum of the first n integers and the sum of the squares of the first n integers, are used to simplify the expressions obtained from translating a definite integral into a Riemann sum, facilitating the evaluation of the integral.
What is the purpose of using a graphing calculator to verify the results of a definite integral?
-Using a graphing calculator to verify the results of a definite integral provides a quick and accurate check of the work done by hand, ensuring the correctness of the solution.
What does the 'dx' in an integral represent?
-The 'dx' in an integral represents the differential element, which corresponds to the width of the rectangles in the Riemann sum as the number of rectangles approaches infinity.

Outlines

00:00

📚 Introduction to Riemann Sums and Definite Integrals

Michelle Krummel introduces the concept of the limiting value of Riemann sums and their connection to definite integrals. She explains the notation and setup for a right Riemann sum, including the function f(x), interval [a, b], and the division of the interval into sub-intervals. The explanation includes how to count the number of rectangles, calculate the width of each rectangle (Δx), and determine the height (f(x_sub_k)) for the right endpoint of each sub-interval. The area of each rectangle is then expressed as width times height, setting the stage for the summation of these areas to find the total area under the curve.

05:02

📈 Summation Notation and Total Area Calculation

The script delves into the summation notation, represented by the Greek letter sigma, to calculate the total area under the curve by adding the areas of all rectangles. It explains how to express the x values as a function of the sub-intervals and how to define the limit of the Riemann sum as the number of rectangles (n) approaches infinity, which leads to the exact area under the curve. The process of translating the Riemann sum into integral notation is also discussed, with the introduction of the elongated 'S' symbol for summation and the dx representing the width of each rectangle.

10:03

🔍 Detailed Explanation of Integral Notation and Examples

The video script provides a detailed explanation of integral notation, showing how to replace the Riemann sum components with their integral counterparts, such as replacing Δx with dx and expressing the function at the kth rectangle as f(x). An example with the function f(x) = x^2 + 2 is used to demonstrate the process of setting up and translating a Riemann sum into an integral. The importance of clearly stating the interval [a, b] in integral notation is highlighted, and the transition from summation to integration is illustrated.

15:04

📝 Matching Riemann Sums to Integral Notation

The script outlines a method for matching a given integral to its corresponding Riemann sum, emphasizing the importance of identifying Δx and the expression for x_sub_k. It provides a step-by-step process for translating the integral of a function from 3 to 5 into a Riemann sum, including calculating Δx, expressing x_sub_k, and substituting these into the integral to form the summation. The use of summation properties is also introduced to simplify the expression before taking the limit as n approaches infinity.

20:06

📉 Summation Properties and Their Application

The video script discusses three key properties of summation: summing a constant, factoring out a constant multiple, and splitting a summation into multiple summations. These properties are essential for evaluating definite integrals and are demonstrated with examples. The script also presents summation formulas for the sum of the first n natural numbers, the sum of their squares, and the sum of their cubes, which are used to simplify the expressions resulting from the Riemann sum before taking the limit.

25:09

🧮 Evaluating Definite Integrals Using Summation Properties

The script provides a detailed example of how to evaluate a definite integral of the function 3x + 1 over the interval [3, 5] using the properties of summation. It walks through the process of translating the integral into a Riemann sum, simplifying the expression algebraically, and then applying the summation properties and formulas to find the limit as n approaches infinity. The result is a numerical value representing the exact area under the curve, which can be verified using a graphing calculator.

30:10

📊 Verifying Definite Integrals with a Graphing Calculator

The script concludes with instructions on how to use a TI-84 Plus graphing calculator to verify the results of definite integrals. It guides the user through entering the integral into the calculator, including the function, the interval [a, b], and the variable of integration. The process of checking the calculated value of 26 for the definite integral of 3x + 1 from 3 to 5 is demonstrated, ensuring the accuracy of the manual calculations performed earlier in the script.

35:11

🔚 Conclusion and Preview of the Fundamental Theorem of Calculus

In the final paragraph, the script wraps up the lesson on Riemann sums and definite integrals, highlighting the importance of understanding the limiting process and its connection to integration. It also provides a preview of the next topic, which is the Fundamental Theorem of Calculus, setting the stage for further exploration into the deeper concepts of calculus.

Mindmap

Keywords

💡Limiting Value

The 'limiting value' in the context of this video refers to the value that a sequence or function approaches as the number of elements in the sequence or the variable of the function approaches infinity. It is central to the concept of the definite integral, as it represents the area under the curve of a function. The script discusses how the limiting value of the Riemann sum defines the definite integral, illustrating this with the process of taking the limit as the number of rectangles (sub-intervals) approaches infinity, making their width approach zero.

💡Riemann Sum

A 'Riemann Sum' is a method for approximating the definite integral of a function by summing the areas of rectangles that lie under the graph of the function. In the video, the concept is introduced as a way to define the definite integral by taking the limiting value of these sums as the number of rectangles increases indefinitely, which is essential for understanding the transition from discrete to continuous quantities in calculus.

💡Definite Integral

The 'definite integral' is a fundamental concept in calculus that represents the signed area under a curve between two points on the x-axis. The video script explains how the definite integral is defined using the limiting value of the Riemann sum, emphasizing its importance in finding the exact area under the curve of a function over a specified interval.

💡Function

In the script, a 'function' is represented by 'f(x)' and is the mathematical rule that describes the relationship between two sets of numbers. The function is integral to the concept of the integral, as the definite integral measures the area under the graph of the function over a given interval. The script uses the function 'f(x)' to demonstrate the process of calculating the definite integral.

💡Sub-intervals

'Sub-intervals' are the smaller divisions of the main interval [a, b] on the x-axis when calculating a Riemann sum. The script explains how the interval from 'a' to 'b' is broken into 'n' equal sub-intervals, each contributing to the sum that approximates the area under the curve of the function.

💡Width of Rectangles

The 'width of rectangles' in the script refers to the horizontal distance between the x-values of the endpoints of each sub-interval. It is a key component in calculating the area of each rectangle in the Riemann sum, with the script noting that as the number of rectangles increases, the width of each rectangle (denoted as 'delta x') approaches zero.

💡Right Riemann Sum

A 'Right Riemann Sum' is a specific type of Riemann sum where the height of each rectangle is determined by the function's value at the right endpoint of each sub-interval. The script discusses the right Riemann sum as a method to approximate the definite integral, highlighting its use in calculating the area under the curve of a function.

💡Sigma Notation

Sigma 'Σ' notation is used in mathematics to represent a summation of a series. In the script, sigma notation is introduced to express the sum of the areas of the rectangles in the Riemann sum, which is then used to define the definite integral through the limiting value as the number of rectangles approaches infinity.

💡Integration

The term 'integration' refers to the process of finding the integral of a function, which, in the context of this video, is synonymous with calculating the definite integral. The script uses integration to describe the process of summing the areas of infinitesimally small rectangles to find the exact area under the curve of a function.

💡Summation Properties

The 'summation properties' are mathematical rules that describe how summations can be manipulated, such as factoring out constants or separating summations into multiple parts. The script explains these properties to simplify the process of evaluating definite integrals by transforming the Riemann sum into a more manageable form.

💡Graphing Calculator

A 'graphing calculator' is an electronic device used to perform mathematical operations, including the evaluation of definite integrals. The script suggests using a graphing calculator, specifically the TI-84 Plus, to verify the results obtained from the manual calculation of definite integrals, demonstrating a practical application of technology in mathematics.

Highlights

Introduction to the concept of the limiting value of the Riemann sum and its use in defining the definite integral.

Explanation of function notation f(x) and setting up a right Riemann sum on a graph.

Breaking down the interval [a, b] into sub-intervals and counting the number of rectangles formed.

Expression for the width of each rectangle in terms of Δx and its simplification.

Different ways to express the width of a rectangle and the concept of equal sub-intervals.

Expression for the height of each rectangle using the function value at the right endpoint.

Generic diagram representing any number of rectangles for better conceptual understanding.

Expression for the area of each rectangle as width times height.

Use of sigma notation to represent the summation of areas of all rectangles.

Detailed explanation of x values as right endpoints of sub-intervals and their relation to Δx.

Defining the Riemann sum expression and taking the limit as n approaches infinity.

Transition from Riemann sum notation to integral notation using the elongated S symbol.

Example of setting up a Riemann sum for a function f(x) = x^2 + 2 over an interval [0, 5].

Properties of summation and their applications in evaluating definite integrals.

Use of summation properties to simplify and evaluate the integral of 3x + 1 from 3 to 5.

Verification of integral results using a graphing calculator for practical application.

Final example involving the integral of (8x - x^2) from 2 to 5 and its step-by-step solution.

Conclusion of the lesson with a preview of the next topic: the Fundamental Theorem of Calculus.

Transcripts

Browse More Related Video

Writing an Integral as a Limit of a Riemann Sum

BusCalc 13.4 Riemann Sums

Riemann Sums and Definite Integrals

The Definite Integral Part II: Using Summation Notation to Define the Definite Integral

What is Integration? Finding the Area Under a Curve

What Is an Integral?

Related Tags

Riemann Sum Definite Integral Calculus Lesson Integral Notation Function Analysis Mathematics Education Limit Concept Area Under Curve Summation Properties Calculus Fundamentals