Kinetic and Potential Energy
TLDRIn this AP Physics essentials video, Mr. Andersen discusses the concepts of kinetic and potential energy, using a wrecking ball and a skateboarder as examples to illustrate the transformation between these two forms of energy. He emphasizes the law of conservation of energy, explaining how the total internal energy remains constant in a closed system, with energy oscillating between potential and kinetic states. The video also introduces a PHET simulation to demonstrate these principles and concludes with a practical problem-solving example, showing how to calculate the potential and kinetic energy of the skateboarder at different points on the ramp.
Takeaways
- 🏋️ Kinetic energy is the energy of motion, while potential energy is due to an object's position.
- 🏢 In a closed system with no energy loss or gain, the conversion between kinetic and potential energy results in the conservation of energy.
- 🏗️ A wrecking ball demonstrates the conversion of gravitational potential energy into kinetic energy when it is released from a crane.
- 🛹 The PHET simulation illustrates the constant total energy in a system as potential energy converts to kinetic energy and vice versa.
- 🔄 The oscillation of energy from potential to kinetic and back is a continuous process in an idealized closed system.
- 🌡️ In reality, the presence of friction converts some of the mechanical energy into thermal energy, causing motion to eventually cease.
- 📐 The potential energy (PE) of an object can be calculated using the formula PE = mgh, where m is mass, g is the gravitational field strength, and h is height.
- 🏎️ At the bottom of a ramp, all potential energy is converted into kinetic energy, which can be calculated using the formula KE = 1/2 mv^2.
- 📐 The speed of the skateboarder at the bottom of the ramp can be determined by equating potential energy to kinetic energy and solving for velocity.
- 🚀 When the skateboarder ascends the ramp, the kinetic energy is converted back into potential energy, allowing for the prediction of his speed and energy at different points.
- 📝 Understanding the conservation of energy and the ability to calculate kinetic and potential energy is crucial for solving problems in physics.
Q & A
What is the main difference between kinetic and potential energy?
-Kinetic energy is the energy of motion, while potential energy is the energy an object has due to its position.
How does the wrecking ball demonstrate the concept of potential energy?
-The wrecking ball has a large mass, and when it is lifted and connected to a crane, it stores a significant amount of gravitational potential energy, which is later converted into kinetic energy when it is released.
What is the role of internal energy in a closed system?
-In a closed system, the total amount of internal energy remains constant during the conversion between kinetic and potential energy.
How does the PHET simulation illustrate the conservation of energy?
-The PHET simulation shows that the total energy, which includes both kinetic and potential energy, remains constant as the skateboarder moves up and down the ramp, converting between the two forms of energy.
What happens to the energy when the coefficient of friction is increased in the simulation?
-When the coefficient of friction is increased, some of the energy is converted into thermal energy, causing the skateboarder to come to rest more quickly.
How can the conservation of energy principle be used to solve problems?
-By understanding that the total internal energy remains constant in a closed system, one can calculate the potential or kinetic energy at different points by knowing the other form of energy and the conditions of the system.
What is the formula for calculating potential energy?
-The formula for potential energy is mgh, where m is mass, g is the gravitational field strength, and h is the height.
How can you find the kinetic energy of an object knowing its potential energy?
-If the system is closed and there is no energy loss, the amount of potential energy an object has can be directly converted into an equivalent amount of kinetic energy.
What is the formula for calculating kinetic energy?
-The formula for kinetic energy is 1/2 mv^2, where m is mass and v is velocity.
How can you determine the velocity of the skateboarder at the bottom of the ramp?
-By equating the potential energy at the top to the kinetic energy at the bottom and using the kinetic energy formula, you can solve for the velocity (v) of the skateboarder.
What would happen if the skateboarder were to go off the edge of the ramp?
-The skateboarder would convert his kinetic energy into potential energy as he ascends, and then back into kinetic energy as he descends, continuing this cycle indefinitely in an ideal scenario without friction.
Outlines
🏋️ Introduction to Kinetic and Potential Energy
This paragraph introduces the concepts of kinetic and potential energy, using the example of a wrecking ball to explain how energy can be stored due to position (potential energy) and released as motion (kinetic energy). The paragraph also touches on the idea of internal energy within a system and the principle of conservation of energy, stating that in a closed system, the total amount of internal energy remains constant as it converts between kinetic and potential forms.
📈 PHET Simulation and Energy Conversion
The paragraph discusses a PHET simulation that illustrates the conversion of potential energy to kinetic energy and vice versa. It uses the example of a skateboarder on a ramp to demonstrate how energy oscillates between these two forms. The simulation shows that in an ideal scenario without energy loss, the total energy remains constant, but in reality, some energy is converted to thermal energy due to friction, causing the skateboarder to eventually come to rest.
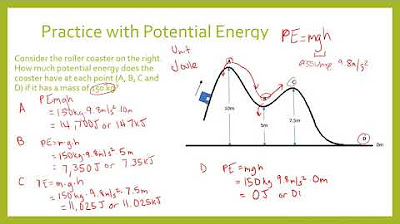
🔢 Calculating Potential and Kinetic Energy
This section focuses on the practical application of calculating potential and kinetic energy. It provides a step-by-step explanation of how to determine the potential energy of a skateboarder at the top of a ramp using the formula mgy (mass times gravitational field strength times height). The paragraph then explains how to calculate the kinetic energy at the bottom of the ramp and the skateboarder's speed using the formula for kinetic energy, 1/2 mv^2.
🚀 Applying Energy Concepts to Real-World Problems
The final paragraph emphasizes the importance of understanding and applying the concepts of kinetic and potential energy in problem-solving. It challenges the viewer to describe and make predictions about internal energy in a closed system and to calculate kinetic energy from potential energy or vice versa, reinforcing the idea that the internal energy of a closed system remains constant as it transitions between potential and kinetic forms.
Mindmap
Keywords
💡Kinetic Energy
💡Potential Energy
💡Conservation of Energy
💡Internal Energy
💡Gravitational Potential Energy
💡Work
💡Mass
💡Acceleration Due to Gravity
💡Friction
💡Skateboarder
💡Wrecking Ball
Highlights
Kinetic energy is the energy of motion, while potential energy is due to an object's position.
A wrecking ball has a large mass and can store significant gravitational potential energy when lifted and connected to a crane.
Upon releasing the crane, the wrecking ball's potential energy is converted into kinetic energy, which is used to do work, such as breaking down a building.
In a system with internal structure, there is internal energy that can be either kinetic or potential.
A closed system does not lose or gain energy, leading to the conservation of energy where the total amount of internal energy remains constant.
The PHET simulation demonstrates the conversion of potential energy to kinetic energy and vice versa, illustrating the conservation of energy principle.
The total energy in the PHET simulation remains constant at 3448 joules, regardless of whether the energy is potential or kinetic.
In nature, systems are not perfectly closed, and energy can be converted into other forms, such as thermal energy due to friction.
By increasing the coefficient of friction in the simulation, the skateboarder's kinetic energy is converted into thermal energy, causing him to come to rest.
The concept of conservation of energy allows for the calculation of potential energy and its conversion into kinetic energy.
A skateboarder at the top of a ramp at 8 meters height has 5900 joules of potential energy, calculated using the formula mgh.
At the bottom of the ramp, the skateboarder's potential energy is fully converted into kinetic energy, also amounting to 5900 joules.
Using the kinetic energy equation (1/2 mv^2), the skateboarder's speed at the bottom can be calculated to be 13 meters per second.
The skateboarder's kinetic energy at a certain point on the ramp can be determined by the energy converted from potential energy.
The skateboarder continues to move and will eventually go flying off the edge of the ramp, demonstrating the continuous conversion of potential to kinetic energy.
The video aims to teach viewers to describe and make predictions about internal energy, as well as to calculate kinetic energy from potential energy or vice versa.
The conservation of energy principle is fundamental in understanding the transformation of energy in closed systems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: