Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (14 of 92) Time & Position Dependencies 3/3

Michel van Biezen
10 Feb 201703:54
EducationalLearning
32 Likes 10 Comments

TLDRIn the third installment of the Electron Line series, the focus shifts to solving the Schrödinger equation for a single particle in one dimension by separating it into position-dependent and time-dependent parts. The constant C, representing the total energy of the particle, is substituted into the position-dependent part, leading to the Time-independent Schrödinger equation. The script explains how the original wave function, a product of position and time-dependent functions, can be expressed as a complex conjugate pair, ultimately resulting in the probability density function. This function, when integrated over all space, should equal one, ensuring normalization and providing the probability distribution of the particle's position, independent of time.

Takeaways
  • 📌 The video discusses the separation of the Schrödinger equation for a single particle in one dimension into parts dependent only on position and time.
  • 🔄 The constant C from the separated equation is identified as the total energy of the particle.
  • 📈 By replacing constant C with the total energy, the position-dependent part of the Schrödinger equation is obtained.
  • 🤹 Multiplying the position-dependent equation by the position-only wave function yields the time-independent Schrödinger equation.
  • 🌐 The time-independent Schrödinger equation simplifies the analysis as it is easier to work with.
  • 🧬 The original wave function, dependent on both position and time, can be expressed as a product of two functions, one for each variable.
  • 💡 The equation for the time-independent wave function was derived in a previous video.
  • 📊 Multiplying the wave function by its complex conjugate results in the probability density function.
  • 🌟 The probability density function must satisfy the normalization condition, integrating to one over all space.
  • 🎯 The normalized probability density function provides the probability distribution of the particle's position, excluding time as a factor.
  • 🔍 The process converts the Schrödinger equation from a time and position dependency to a position-only dependency, simplifying the problem.
Q & A

  • What is the main topic of the third video in the series?

    -The main topic of the third video is the separation of the Schrödinger equation for a single particle in one dimension into parts that depend only on position and parts that depend only on time.

  • How does the constant C in the Schrödinger equation relate to the particle's energy?

    -The constant C in the Schrödinger equation is equal to the total energy of the particle, as demonstrated by the wave equation that depends only on time.

  • What is the Time-independent Schrödinger equation?

    -The Time-independent Schrödinger equation is a differential equation that describes a particle moving in one dimension, where the equation is no longer dependent on time. It is derived by replacing the constant C with the total energy of the particle in the position-dependent part of the original Schrödinger equation.

  • How is the original wave function related to the wave functions that depend only on position and time?

    -The original wave function, which depends on both position and time, can be written as a product of a wave function that depends only on position and a wave function that depends only on time.

  • What is the significance of multiplying the time-independent Schrödinger equation by the position-dependent wave function?

    -Multiplying the time-independent Schrödinger equation by the position-dependent wave function results in a negated term, which simplifies the equation and makes it easier to work with.

  • What is the complex conjugate in the context of the wave function?

    -The complex conjugate refers to the alteration of the negative 'i' to a positive 'i' in the exponent of the wave function parts that depend only on position and time. This concept is used to derive the probability density function.

  • How does the probability density function relate to the wave function and its complex conjugate?

    -The probability density function is derived by multiplying the wave function that depends on both position and time by its complex conjugate. This product represents the probability distribution of the particle's position.

  • What condition must the probability density function meet when integrated over all space?

    -The probability density function must satisfy the condition that when integrated over all space, from negative infinity to infinity, the integral equals one. This ensures that the total probability over all possible locations is 100%.

  • Why is normalizing the probability density function important?

    -Normalizing the probability density function is important because it ensures that the area under the curve, representing the total probability, equals one. This allows for a meaningful interpretation of the function as a probability distribution.

  • What is the result of normalizing the probability density function?

    -After normalizing the probability density function, we obtain a function that describes the probability of finding the particle at a particular position, with time no longer being a factor.

  • How does the process described in the video simplify the analysis of the Schrödinger equation?

    -By converting the Schrödinger equation from one that depends on both time and position to one that only depends on position, the resulting Time-independent Schrödinger equation is much simpler to solve and analyze.

Outlines
00:00
🌟 Separation of the Schrödinger Equation

This paragraph introduces the second part of the video series on the Schrödinger equation for a single particle in one dimension. It explains the separation of the equation into parts that depend only on position and those that depend only on time. The constant C, representing the total energy of the particle, is introduced and its significance is discussed. The paragraph then describes the process of multiplying the position-dependent part of the equation by the wave function, leading to the time-independent Schrödinger equation. The concept of the probability density function and its normalization to ensure that the integral over all space equals one is also explained, emphasizing the transition from a time and position-dependent equation to one that only depends on position.

Mindmap
Keywords
💡Schrödinger Equation
The Schrödinger Equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes with time. In the video, the equation is initially presented for a single particle in one dimension, and then separated into parts that depend only on position and parts that depend only on time. This separation is crucial for simplifying the equation and understanding the behavior of the particle.
💡Total Energy
Total energy, in the context of the video, refers to the sum of kinetic and potential energy of a particle. The constant 'C' in the separated Schrödinger Equation is identified as the total energy of the particle. This concept is central to the wave equation that only depends on time, which is used to show the relationship between the constant and the energy of the particle.
💡Wave Function
A wave function is a mathematical description of the quantum state of a system. In the video, the wave function is used to describe the quantum state of a particle in terms of both its position and time. The wave function is also used to define the probability density function, which gives the probability of finding the particle at a particular position.
💡Time-Independent Schrödinger Equation
The time-independent Schrödinger equation is a simplified form of the full Schrödinger equation that only considers the spatial part of the quantum state, not the temporal evolution. By separating the time-dependent and position-dependent parts, the video demonstrates how to arrive at this simpler equation, which is easier to solve and provides insights into the stationary states of a quantum system.
💡Complex Conjugate
The complex conjugate of a complex number or function is obtained by changing the sign of the imaginary part. In the context of the video, the complex conjugate of the wave function is used when multiplying the wave function that depends on both position and time to derive the probability density function.
💡Probability Density Function
The probability density function (PDF) is a function that describes the relative likelihood for a particle to be found at a certain position. In quantum mechanics, the square of the absolute value of the wave function represents the PDF. The video emphasizes the importance of normalizing this function so that its integral over all space equals one, ensuring that the total probability of finding the particle anywhere is 100%.
💡Normalization
Normalization is the process of adjusting a function or set of data so that it satisfies certain constraints, such as the sum of all its values being equal to one. In the context of the video, the wave function must be normalized so that its integral, representing the probability of finding the particle, sums up to one over all possible positions.
💡Position and Time
In the video, position and time are the two fundamental variables that describe the state of a quantum particle. The separation of the Schrödinger Equation into parts dependent on position and time allows for a more manageable analysis of the system. The video also discusses how the wave function can be separated into components that depend only on position and those that depend only on time.
💡Differential Equation
A differential equation is an equation that relates a function with its derivatives. In the context of the video, the time-independent Schrödinger equation is a differential equation that describes the spatial part of the quantum state. Solving this equation yields the wave functions that are stationary states of the system.
💡Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at very small scales, such as atomic and subatomic particles. The video's content is centered around the mathematical framework of quantum mechanics, specifically focusing on the Schrödinger Equation and wave functions to understand the quantum states of particles.
💡Stationary States
In quantum mechanics, stationary states are states of a quantum system that do not change over time. The time-independent Schrödinger equation is used to find these states, which are characterized by wave functions that are solutions to the equation and do not depend on time. These states are of particular interest because they represent stable configurations of the system.
Highlights

The video is the third in a series on electron behavior.

The focus is on separating the Schrödinger equation for a single particle in one dimension.

The equation is divided into parts dependent only on position and parts dependent only on time.

The constant C in the equation is identified as the total energy of the particle.

The constant C is replaced with the total energy in the position-dependent part of the equation.

The wave function is multiplied by the position-dependent part of the equation.

This results in the time-independent Schrödinger equation for a particle in one dimension.

The original wave function is a product of position-dependent and time-dependent functions.

The equation for the time-dependent wave function was derived in a previous video.

The complex conjugate of the position-dependent wave function is introduced.

The product of the wave function and its complex conjugate is equivalent to the wave equation multiplied by the complex conjugate.

The probability density function is derived from the product of the wave function and its complex conjugate.

The probability density function must integrate to one over all space.

Normalization of the probability density function is discussed.

The normalized probability function provides the location of the particle as a function of position only.

The process simplifies the Schrödinger equation by eliminating time as a factor.

Examples will be provided to illustrate the conversion from a time and position-dependent to a position-only dependent Schrödinger equation.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (13 of 92) Time & Position Dependencies 2/3

Schrodinger Equation - A simple derivation

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (15 of 92) Time & Position Dependencies Ex.*

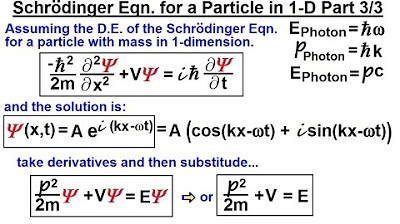
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (7 of 92) The Schrodinger Eqn. in 1-D (3/3)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (12 of 92) Time & Position Dependencies 1/3

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (2 of 92) Normalization of the Wave Equation

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsSchrodingerEquationWaveFunctionsParticlePhysicsTimeIndependenceMathematicalAnalysisPhysicsEducationProbabilityDensityOneDimensionTotalEnergy