The Gradient of a Function (Calculus 3)

Houston Math Prep

8 Mar 202117:22

EducationalLearning

32 Likes 10 Comments

TLDRThis video from Houston Math Prep delves into the concept of gradients, explaining their significance in multi-variable calculus. The gradient, represented by the del operator, is a vector that indicates the direction of the greatest rate of increase for a scalar function. The tutorial covers how to calculate the gradient for functions of two and three variables, using examples to illustrate the process. It also discusses the magnitude of the gradient, which reflects the steepness of the increase, and touches on finding directions of greatest increase, decrease, and no change on a function's surface.

Takeaways

📚 The video is an educational resource from Houston Math Prep, focusing on explaining the concept of gradients in multi-variable calculus.
🔍 The gradient, denoted by 'nabla' or 'del', is a vector that points in the direction of the greatest increase of a scalar function at a given point.
📈 The gradient operation is applied to scalar functions, but the result is a vector function, indicating the direction of steepest ascent on a surface.
📝 For a function of two variables, the gradient is calculated using partial derivatives with respect to each variable, resulting in a two-component vector.
📉 The gradient can also be extended to functions of three variables, resulting in a three-component vector, indicating direction in 3D space.
🌐 The magnitude of the gradient vector represents the rate of increase at a point, with larger magnitudes indicating steeper ascents.
📌 The direction of the gradient is always perpendicular to the level curves of the function and points towards the direction of the greatest increase.
🧭 The gradient at a specific point is found by substituting the coordinates of that point into the gradient vector function.
🔄 The gradient vector can be normalized to a unit vector to provide a direction without regard to the rate of increase.
📐 The orthogonal direction to the gradient, where there is no increase or decrease, can be found by considering vectors perpendicular to the gradient.
🔑 The script also mentions an upcoming video on directional derivatives, which will explore how to find rates of change in any given direction using the gradient.

Q & A

What is the gradient in the context of multi-variable calculus?
-The gradient is a vector function that represents the direction of the greatest increase of a scalar function at any given point in multi-variable calculus. It is denoted by the symbol 'nabla' or 'del' and is calculated as the partial derivatives of the function with respect to each variable.
How is the gradient of a scalar function represented mathematically?
-The gradient of a scalar function is represented as the vector function with components being the partial derivatives of the function with respect to each variable. For a function of two variables, it is represented as del f = (∂f/∂x, ∂f/∂y).
What does the gradient vector at a point on a function indicate?
-The gradient vector at a point on a function indicates the direction of the steepest ascent at that point. It points towards the direction where the function increases the most rapidly.
How does the gradient change when considering a function of three variables instead of two?
-When considering a function of three variables, the gradient remains a vector function but now has three components, with the third component being the partial derivative of the function with respect to the third variable, z.
What is the gradient of the function f(x, y) = x^2 + y^2?
-The gradient of the function f(x, y) = x^2 + y^2 is del f = (2x, 2y), which means the gradient vector at any point (x, y) is proportional to the position vector (x, y).
How do you find the gradient of a function at a specific point?
-To find the gradient of a function at a specific point, you evaluate the gradient vector function at that point by substituting the coordinates of the point into the components of the gradient vector.
What is the relationship between the gradient and the level curves of a function?
-The gradient is always perpendicular to the level curves of a function. It points in the direction of the greatest increase, which is normal to the level curve at any point.
How does the magnitude of the gradient vector relate to the rate of increase of a function?
-The magnitude of the gradient vector represents the rate of the greatest increase of the function. A larger magnitude indicates a steeper ascent, while a smaller magnitude indicates a gentler slope.
What is the gradient of the function f(x, y) = sqrt(36 - x^2 - y^2) at the point (-3, 2)?
-The gradient of the function at the point (-3, 2) is calculated by substituting x and y into the gradient vector, resulting in a vector with components (3/√23, -2/√23) after simplification.
How can you find a direction of no change (i.e., a direction tangent to the level curve) at a given point on a function?
-To find a direction of no change, you need a vector that is orthogonal to the gradient at that point. This means the dot product of the gradient vector and the direction vector should be zero. A common approach is to find a vector that, when dotted with the gradient, yields zero, and then normalize this vector to get a unit vector in that direction.

Outlines

00:00

📚 Introduction to Gradients in Multivariable Calculus

This paragraph introduces the concept of gradients in the context of multivariable calculus. It explains that the gradient of a scalar function, represented by the del or nabla symbol, indicates the direction of the greatest increase at any given point on the function. The gradient is computed as a vector function with components derived from partial derivatives with respect to each variable. The paragraph provides an example of a function of x and y, calculates the gradient, and evaluates it at specific points to demonstrate how the gradient changes direction depending on the location on the function's surface.

05:00

🔍 Calculating Gradients and Their Magnitude

This section delves deeper into calculating the gradient of a function and interpreting its magnitude. It explains the process of finding the gradient for a given function, which involves taking partial derivatives with respect to each variable. The paragraph also discusses evaluating the gradient at a specific point, illustrating how to find the direction and rate of the greatest increase or decrease. It uses an example involving the square root of a quadratic expression to demonstrate these concepts and shows how the gradient vector always points towards the origin for that particular function, indicating the direction of steepest ascent.

10:01

🧭 Direction of Greatest Increase and Decrease

The third paragraph focuses on determining the direction and rate of the greatest increase and decrease for a given function at a specific point. It explains how the gradient vector points in the direction of the steepest ascent and how its magnitude represents the rate of this increase. The paragraph provides a method to find the unit vector in the direction of the gradient for clarity and uses another function to demonstrate the process of finding the gradient, its evaluation at a point, and the calculation of the magnitude to determine the rate of increase. It also discusses the concept of the direction of greatest decrease, which is the opposite direction of the gradient.

15:02

🌐 Finding Directions of No Change and Orthogonality

The final paragraph discusses the concept of finding a direction of no change on a function's surface, which is orthogonal to the gradient. It explains that moving in this direction would not result in any increase or decrease in the function's value, effectively staying on the same level curve. The paragraph provides a method to find such a direction by ensuring the dot product between the gradient and another vector is zero, indicating orthogonality. It uses a specific function to demonstrate how to find this direction, normalize it to a unit vector, and discusses the implications of moving in an orthogonal direction to the gradient.

Mindmap

Keywords

💡Gradient

The gradient is a fundamental concept in multivariable calculus that represents the direction of the greatest rate of increase of a scalar function at any given point. In the video, the gradient is introduced as a vector function, denoted by the symbol 'del' or 'nabla,' which provides a direction for the steepest ascent on a surface defined by the scalar function. For example, when calculating the gradient of the function \( z = f(x, y) \), the script describes how to find the partial derivatives with respect to \( x \) and \( y \), which form the components of the gradient vector.

💡Scalar Function

A scalar function is a mathematical function that maps a set of input values to a single output value, as opposed to a vector function, which maps to a set of output values. In the context of the video, the gradient of a scalar function is discussed, emphasizing that the gradient itself is a vector, even though it operates on a scalar function. The script uses the function \( z = x^2 + y^2 \) to illustrate how to calculate the gradient.

💡Partial Derivative

A partial derivative is the derivative of a function with respect to one of its variables, while treating the other variables as constants. The video script explains how to calculate partial derivatives as part of the process of finding the gradient of a function. For instance, when finding the gradient of \( f(x, y) \), the partial derivatives with respect to \( x \) and \( y \) are computed to determine the x and y components of the gradient vector.

💡Nabla

Nabla, represented by the symbol 'del', is the notation used to denote the gradient of a scalar function. It is used in the script to introduce the concept of the gradient and to describe its calculation. The script mentions that while 'nabla' is the formal term, 'del' is more commonly used in discussions of calculus and vector calculus.

💡Vector Function

A vector function is a function that maps its inputs to a vector of outputs. In the video, the gradient is described as a vector function that results from the operation on a scalar function. The script explains that while the input to the gradient operation is a scalar function, the output is a vector that indicates the direction of the greatest increase on the surface defined by the scalar function.

💡Direction of Greatest Increase

The direction of greatest increase refers to the direction in which a function increases at the fastest rate at a given point. The video script explains that the gradient vector points in this direction. For example, when evaluating the gradient at a specific point, such as (2,1), the resulting vector indicates the direction in which to move to ascend the surface most steeply from that point.

💡Level Curves

Level curves are curves on a graph that represent points of equal value for a function, similar to contour lines on a map. The script mentions level curves to illustrate how the gradient is perpendicular to these curves in the direction of increasing function values. This concept is used to explain the relationship between the gradient and the direction of no change on the surface.

💡Magnitude

In the context of the video, the magnitude of the gradient refers to the length of the gradient vector, which indicates the rate of increase of the function. The script explains that a larger magnitude suggests a steeper ascent on the surface, whereas a smaller magnitude indicates a gentler slope. The magnitude is calculated using the square root of the sum of the squares of the vector's components.

💡Unit Vector

A unit vector is a vector with a magnitude of one, often used to represent direction without regard to scale. The video script discusses converting the gradient vector into a unit vector to represent the direction of greatest increase in a normalized form. This is done by dividing the gradient vector by its magnitude, as illustrated when finding the unit vector for the direction of greatest increase at the point (1, -1).

💡Orthogonal

Orthogonality in the context of vectors means that two vectors are perpendicular to each other, having a dot product of zero. The script explains how to find a direction of no change by identifying a vector orthogonal to the gradient, which would lie along a level curve. The concept is used to determine a direction where the function's value does not increase or decrease, staying constant along that path.

💡Directional Derivative

Although not explicitly defined in the script, the concept of the directional derivative is mentioned as a topic for a future video. A directional derivative is the rate of change of a scalar function in a particular direction at a given point. It is related to the gradient in that the gradient provides the direction of the greatest rate of increase, and the directional derivative can be calculated using the gradient and a unit vector in any chosen direction.

Highlights

The video explains the concept of gradients in the context of multi-variable calculus.

Gradients indicate the direction of greatest increase for a scalar function at a given point.

The gradient is represented by the del or nabla symbol and is a vector function.

For a function of two variables, the gradient has two components: partial derivatives with respect to x and y.

In a 3D space, the gradient of a function has three components, including the partial derivative with respect to z.

The first example demonstrates calculating the gradient of a function f(x, y) = x^2 + y^2.

The gradient at a specific point is found by substituting the point's coordinates into the gradient vector function.

The gradient's direction at a point can vary, indicating different directions of greatest increase.

The magnitude of the gradient vector represents the steepest rate of increase at a point.

The second example involves a function f(x, y) = sqrt(36 - x^2 - y^2) and its gradient calculation.

The gradient of the second example function always points toward the origin, indicating the direction of steepest ascent.

The gradient's magnitude near the origin is smaller, indicating a less steep uphill climb.

The third example explores the function f(x, y) = x^2y - xy^2 and its gradient at the point (1, -1).

The gradient's direction and rate of greatest increase are derived from the gradient vector at a specific point.

The direction of greatest decrease is the opposite of the gradient's direction of greatest increase.

A direction of no change is found by identifying a vector orthogonal to the gradient, resulting in a dot product of zero.

The video concludes with a preview of the next topic: directional derivatives and their application using gradients.

Transcripts

Browse More Related Video

Directional Derivatives (Calculus 3)

Why the gradient is the direction of steepest ascent

Divergence and Curl (Vector Fields)

Gradient 1 | Partial derivatives, gradient, divergence, curl | Multivariable Calculus | Khan Academy

Tensor Calculus 2: The Two Conflicting Definitions of the Gradient

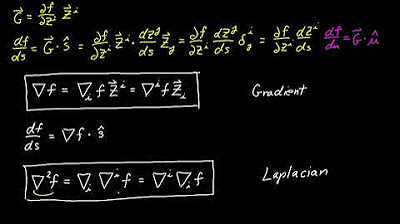
Video 39 - Gradient