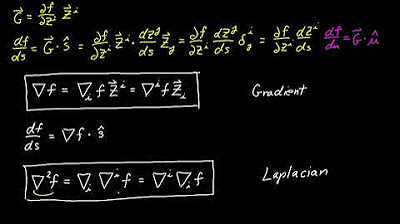Directional derivative

Khan Academy
11 May 201607:14
EducationalLearning
32 Likes 10 Comments

TLDRThis script introduces the concept of the directional derivative, extending the idea of partial derivatives for multivariable functions. It explains how to measure the rate of change of a function in a specific direction, using a vector to represent that direction. The video illustrates the process of taking a 'nudge' along the vector and calculating the resulting change in the function's output, emphasizing the limit as the nudge approaches zero. The formula for the directional derivative is presented, highlighting its calculation as a dot product between the gradient of the function and the direction vector, offering a flexible approach applicable to functions of any number of variables.

Takeaways
  • 📚 The directional derivative extends the concept of partial derivatives, which are used to measure the rate of change of a function with multiple variables.
  • 📐 Partial derivatives focus on the rate of change in the x or y direction at a specific point in the input space, like (1,2), by considering an 'nudge' in that direction.
  • 🧭 Directional derivatives consider the rate of change in any given direction specified by a vector, such as the vector v = <-1, 2>.
  • 🔍 The concept involves taking a very small step, denoted by 'h', in the direction of the vector and examining the resulting change in the output space.
  • 📉 The formula for the directional derivative involves multiplying the components of the vector by the respective partial derivatives and summing them up.
  • 📝 The general formula for the directional derivative of a function 'f' in the direction of vector 'w = <a, b>' is a*(∂f/∂x) + b*(∂f/∂y).
  • 🔄 The directional derivative can also be expressed as the dot product between the vector 'w' and the gradient of 'f', which is a more compact and general form.
  • 📚 The gradient itself is a vector of partial derivatives, which points in the direction of the steepest ascent of the function.
  • 🌐 The concept of the directional derivative is flexible and can be applied to functions with more than two variables, making it a powerful tool in multivariable calculus.
  • 📈 Understanding directional derivatives is crucial for analyzing how functions behave as you move in various directions within their domain.
  • 🔑 The script hints at a follow-up video that will provide a formal definition of the directional derivative, suggesting the importance of a rigorous mathematical understanding.
Q & A

  • What is the directional derivative?

    -The directional derivative is a concept that extends the idea of a partial derivative. It measures the rate at which a function changes in a specific direction at a given point in its domain.

  • What is the difference between a partial derivative and a directional derivative?

    -A partial derivative measures the change in a function's value with respect to one variable while holding the other variables constant. A directional derivative, on the other hand, considers the change in the function's value in a specific direction, which is defined by a vector.

  • What is the significance of the vector in the context of directional derivatives?

    -The vector in the context of directional derivatives represents the direction in which the change in the function's value is being measured. It is used to determine the rate of change along that direction at a specific point.

  • How is the directional derivative related to the gradient of a function?

    -The directional derivative can be expressed as the dot product of the gradient of the function and the unit vector in the direction of interest. This shows that the directional derivative is directly related to the rate and direction of the steepest ascent or descent of the function at a point.

  • What does the 'nudging' in the x and y directions signify in the context of partial derivatives?

    -The 'nudging' in the x and y directions is a conceptual way to describe the process of taking partial derivatives. It refers to making a small change in the x or y direction and observing the resulting change in the function's output.

  • What is the role of the limit in calculating the directional derivative?

    -The limit is used in calculating the directional derivative to consider the behavior of the function as the step size (h) approaches zero, which allows for the determination of the instantaneous rate of change in the specified direction.

  • How is the directional derivative calculated for a function with two variables?

    -For a function with two variables, the directional derivative in the direction of a vector \(\vec{v} = (a, b)\) is calculated as \(a \cdot \frac{\partial f}{\partial x} + b \cdot \frac{\partial f}{\partial y}\), where \(\frac{\partial f}{\partial x}\) and \(\frac{\partial f}{\partial y}\) are the partial derivatives of the function with respect to x and y, respectively.

  • What is the meaning of the notation ∇f(v) for the directional derivative?

    -The notation ∇f(v) represents the directional derivative of the function f in the direction of the vector v. The ∇ symbol denotes the gradient, and the vector v specifies the direction in which the derivative is taken.

  • Can the concept of directional derivatives be extended to functions with more than two variables?

    -Yes, the concept of directional derivatives can be extended to functions with more than two variables. The general formula involves taking the dot product of the gradient vector (which has as many components as there are variables) and the direction vector.

  • What is the practical significance of understanding directional derivatives?

    -Understanding directional derivatives is important in various fields such as physics, engineering, and economics, where it helps in determining the rate of change of a function in a specific direction, which can be useful for optimization and understanding the behavior of multivariable systems.

Outlines
00:00
📘 Introduction to Directional Derivatives

The concept of directional derivatives extends the idea of partial derivatives. Partial derivatives deal with functions that have multi-variable inputs, typically with two inputs and a single output. The focus here is on understanding how a function changes as its input is nudged in specific directions (x or y). The directional derivative examines the change in the function when nudged along a given vector, treating these nudges as infinitesimally small, and using limits to determine the resulting change.

05:03
🔍 Calculating Directional Derivatives

To calculate the directional derivative, one considers a vector (e.g., [-1, 2]) and explores the function's change when nudged in that direction. The key idea is that the directional derivative is not about taking a significant step but rather an infinitesimally small one, denoted by h. The directional derivative formula involves a dot product of the vector with the function's gradient, simplifying to a · ∂f/∂x + b · ∂f/∂y, where a and b are the vector's components. This approach is versatile and can be generalized for functions with higher-dimensional inputs.

Mindmap
Keywords
💡Directional Derivative
The directional derivative is a concept in vector calculus that extends the idea of a partial derivative to measure the rate of change of a multivariable function in a specific direction. In the video, it is introduced as a way to understand how a function's output changes when 'nudged' in a particular direction defined by a vector. The script uses the directional derivative to illustrate the sensitivity of a function's output to changes in its input variables along a given vector, such as moving 'negative one step in the x-direction and two steps in the y-direction'.
💡Partial Derivative
A partial derivative is a derivative taken with respect to one variable of a function of multiple variables. In the context of the video, partial derivatives are used to measure the rate at which the output of a function changes with respect to a single input variable, while holding the other variables constant. The script mentions partial derivatives as a precursor to understanding the concept of directional derivatives, specifically when considering 'nudging' in the x or y direction.
💡Multivariable Function
A multivariable function is a function that takes more than one input variable to produce an output. The video script discusses multivariable functions in the context of partial and directional derivatives, where the function's behavior with respect to changes in two inputs, x and y, is considered. The script uses the example of a function that takes x and y as inputs and produces a single real number output.
💡Input Space
In the script, the input space refers to the set of all possible values that the input variables of a function can take. It is typically represented as a coordinate plane, such as the x and y plane for functions with two input variables. The concept is used to visualize the starting point for calculating derivatives, where 'nudging' in various directions within this space helps to understand the function's behavior.
💡Output Space
The output space is the set of all possible values that a function can produce. In the video, the output space is described as the real numbers, which is where the function's output is directed. The script discusses how the directional derivative relates to the change in the output space when there is a small change in the input space.
💡Vector
A vector in the context of the video is a direction in the input space, represented by an ordered pair of numbers, such as (-1, 2). The script uses vectors to define the direction in which the function is 'nudged' to calculate the directional derivative. The vector is essential for understanding the directional change in the function's output.
💡Nabla
Nabla, represented by the symbol '∇', is a symbol used in mathematics to denote the gradient of a function. In the script, nabla is used to represent the directional derivative notation, where it is placed with the function and the vector to indicate the derivative in the direction of the vector. The script explains that this notation is indicative of the calculation method for the directional derivative.
💡Gradient
The gradient is a vector of partial derivatives of a function with respect to each of its variables. In the video script, the gradient is used to compactly represent the directional derivative as a dot product between the gradient vector and the direction vector. The script mentions that the gradient is a generalization that makes the concept of directional derivatives applicable to functions with more than two variables.
💡Dot Product
The dot product is a mathematical operation that takes two vectors and returns a single number, representing the product of the magnitudes of the vectors and the cosine of the angle between them. In the script, the dot product is used to express the directional derivative as the product of the gradient vector and the direction vector, simplifying the calculation and understanding of the rate of change in a given direction.
💡Limit
In calculus, a limit is the value that a function or sequence approaches as the input approaches some value. The script discusses the concept of taking the limit as the 'nudge' along the direction vector becomes infinitesimally small, which is crucial for defining the directional derivative accurately.
💡Ratio
The ratio in the context of the video refers to the relationship between the change in the function's output and the change in the input variables. Specifically, the script describes how the directional derivative is calculated as the ratio of the change in the output space to the change in the input space when moving in a specific direction.
Highlights

Introduction to the concept of the directional derivative as an extension of the idea of partial derivatives.

Explanation of partial derivatives in the context of multi-variable functions with single or vector variable outputs.

Visualization of the input space (x, y-plane) and the concept of outputting to real numbers or a transformation.

Illustration of taking the partial derivative at a specific point by considering a nudge in the x-direction.

Discussion on the ratio between the size of the resulting nudge in the output space and the original nudge in the input space.

Introduction of the directional derivative considering a vector v with components affecting the function's output.

Description of the vector v as a step in both x and y directions and its impact on the function.

Concept of taking a very small step (h) along the vector direction to find the directional derivative.

Explanation of the limit as h approaches zero to find the ratio of changes in the output to the input.

Introduction of the notation for the directional derivative, using the nabla symbol and the vector v.

Different notations for directional derivatives and the preference for the nabla notation due to its clarity.

Calculation of the directional derivative using the components of the vector and the partial derivatives.

General formula for the directional derivative in terms of vector components a and b, and partial derivatives.

Interpretation of the directional derivative as a measure of how a tiny nudge in the vector direction changes the output.

Alternative representation of the directional derivative using the dot product and the gradient vector.

Flexibility of the directional derivative formula for higher dimensions beyond two.

Upcoming formal definition of the directional derivative in the next video.

Transcripts

Browse More Related Video

Directional derivative, formal definition

Directional Derivatives | What's the slope in any direction?

Directional derivatives and slope

Directional Derivatives (Calculus 3)

Why the gradient is the direction of steepest ascent

Video 39 - Gradient

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Directional DerivativePartial DerivativeMulti-variableMathematicsVector AnalysisFunction GradientInput SpaceOutput SpaceLimit ConceptDot ProductEducational Content