Calculus 3: Directional Derivatives and the Gradient Vector (Video #16) | Math with Professor V
TLDRThis calculus video lecture delves into the concept of directional derivatives and the gradient vector. It explains how partial derivatives relate to the rate of change in specific directions and introduces the directional derivative for arbitrary directions using unit vectors. The lecture demonstrates how to calculate directional derivatives with examples, highlights the gradient's role in finding the maximum rate of change, and discusses its applications in determining tangent planes and normal lines to surfaces. The script concludes with a problem-solving approach to find points where a tangent plane is parallel to a given plane, showcasing the gradient's utility in multivariable calculus.
Takeaways
- 📚 Directional derivatives provide the rate of change of a function in a specified direction, not limited to the axes' directions.
- 📐 Unit vectors are essential in defining the direction for calculating directional derivatives.
- 🔍 The process of finding a directional derivative involves considering a line in the desired direction, selecting points on that line, and examining the rate of change between these points.
- 📈 The average rate of change is calculated by the difference in the function's values at two points divided by the distance between them.
- 🚀 The instantaneous rate of change, or the derivative, is found by taking the limit of the average rate of change as the distance between points approaches zero.
- 📘 A theorem states that if a function is differentiable, its directional derivative in the direction of a unit vector can be computed as the dot product of the gradient vector and the unit vector.
- 📉 The gradient vector is a function of the partial derivatives with respect to each variable and points in the direction of the greatest rate of increase of the function.
- 🌡 The magnitude of the gradient vector represents the rate of the fastest increase of a function, and its direction is where the function increases most rapidly.
- 📊 Directional derivatives can be represented as a dot product between the gradient vector and a unit vector in the desired direction.
- 🧭 The gradient vector is orthogonal to level curves of the function, which means it is perpendicular to any tangent on the level curve at a given point.
- 🔗 The gradient vector is used to find the equation of tangent planes to surfaces and the direction of normal lines, simplifying calculations in multivariable calculus.
Q & A
What is the purpose of directional derivatives in calculus?
-Directional derivatives are used to find the rate of change of a function in a specific direction, rather than just along the x or y axes. They are useful for understanding how a quantity, such as temperature or elevation, changes as you move in various directions across a surface.
How are unit vectors used in the context of directional derivatives?
-Unit vectors are used to describe the direction in which the rate of change is being measured. They have a magnitude of 1 and are used to scale the directional derivative formula to reflect the specific direction of interest.
What is the process to find the directional derivative of a function at a given point in a specific direction?
-The process involves finding the unit vector in the direction of interest, determining the partial derivatives of the function with respect to each variable, evaluating these partial derivatives at the given point, and then using the dot product of the gradient vector and the unit vector to find the directional derivative.
What is the gradient vector in calculus, and how is it related to directional derivatives?
-The gradient vector is a vector of partial derivatives of a function with respect to each variable. It points in the direction of the greatest rate of increase of the function. The directional derivative can be found by taking the dot product of the gradient vector and a unit vector in the direction of interest.
Can you provide an example of how to find the directional derivative of a function f(x, y) at a point (x₀, y₀) in the direction of a unit vector with components (a, b)?
-To find the directional derivative, first ensure the vector (a, b) is a unit vector. Then, find the partial derivatives of f with respect to x and y, evaluate these at the point (x₀, y₀), and multiply the partial derivative with respect to x by 'a' and the partial derivative with respect to y by 'b'. The sum of these products is the directional derivative in the direction of the unit vector.
What does the magnitude of the gradient vector represent?
-The magnitude of the gradient vector represents the maximum rate of change of the function. It is the steepest rate at which the function's value increases in any direction.
How can you determine the direction in which a function increases the fastest at a given point?
-The function increases the fastest in the direction of the gradient vector at the given point. This is because the gradient vector points in the direction of the greatest rate of increase.
What is the physical interpretation of the directional derivative in the context of a temperature distribution over a surface?
-In the context of a temperature distribution, the directional derivative represents the rate at which the temperature changes as you move in a specific direction across the surface. It tells you how quickly the temperature is rising or falling in that direction.
Can the gradient vector be used to find the equation of a tangent plane to a surface?
-Yes, the gradient vector can be used to find the equation of a tangent plane to a surface. The gradient vector acts as the normal vector to the tangent plane, and by using a point on the surface, the equation of the tangent plane can be determined.
What is the significance of the gradient vector being orthogonal to the level curves of a function?
-The orthogonality of the gradient vector to the level curves indicates that the gradient is always perpendicular to the surface at any point, which is a key property used in finding tangent planes and understanding the local behavior of the function.
Outlines
📚 Introduction to Directional Derivatives and Gradient Vector
This paragraph introduces the concept of directional derivatives and the gradient vector in the context of calculus. It explains how partial derivatives provide the rate of change in the direction of the x or y axis, and how directional derivatives extend this to any arbitrary direction using unit vectors. The process involves finding the derivative of a function at a point in the direction of a unit vector, which is done by considering two points on a line with the same direction as the unit vector and taking the limit as the distance between these points approaches zero. The paragraph sets the stage for further exploration of these concepts.
🔍 The Directional Derivative Theorem and Its Computation
The second paragraph delves into the theorem that allows for the computation of the directional derivative without directly using the limit definition, which is often impractical. It states that if a function is differentiable and has partial derivatives with respect to x and y, then the directional derivative in the direction of a unit vector with components (a, b) can be found by multiplying the partial derivatives by the respective components of the unit vector. This simplifies the process and provides a clear formula for calculation. The paragraph also illustrates this with an example, showing how to find the directional derivative of a function at a specific point in a given direction.
📉 Directional Derivatives in Practice and Gradient Vectors
This paragraph discusses the practical application of directional derivatives and introduces the concept of the gradient vector. It explains how the directional derivative can be represented as a dot product between the gradient vector and a unit vector in the direction of interest. The gradient vector is defined as the vector of partial derivatives with respect to each variable. The paragraph also explores how the magnitude of the directional derivative changes with the angle between the unit vector and the gradient vector, highlighting the maximum and minimum values these derivatives can take.
🔄 Directional Derivatives and the Gradient's Applications
The fourth paragraph continues the discussion on the applications of the gradient vector, emphasizing its role in finding the direction of the greatest rate of increase of a function. It presents a theorem that states the maximum value of the directional derivative is given by the magnitude of the gradient vector when the unit vector is in the same direction as the gradient. The paragraph also provides an example of how to find the rate of change of temperature at a point in a given direction, demonstrating the process of calculating the gradient and using it to find the directional derivative.
🌡️ Temperature Gradient and Directional Derivatives in Three Dimensions
This paragraph extends the concept of directional derivatives to three-dimensional functions, such as temperature in a three-dimensional space. It explains how to find the rate of change of temperature at a point in the direction of another point, by creating a unit vector in that direction and using the gradient of the temperature function. The example provided shows how to calculate the gradient at a specific point and then use it to find the directional derivative towards another point, illustrating the process with a clear step-by-step approach.
⛰️ Hill Climbing and Gradient Vectors in Elevation
The sixth paragraph presents a scenario where the shape of a hill is given by an equation relating x, y, and z coordinates, and the task is to determine whether one ascends or descends when walking in a certain direction, as well as the rate of this change. It explains how to find the gradient of the hill's elevation function and how to use it to calculate the directional derivative, which indicates the rate of change in elevation when moving in a specific direction. The paragraph also discusses how to find the direction in which the temperature increases the fastest at a given point.
📉 Gradient Vectors and the Maximum Rate of Change
This paragraph focuses on the relationship between gradient vectors and the maximum rate of change of a function. It explains that the maximum rate of increase of a function at a point is given by the magnitude of the gradient vector at that point, and this occurs when the direction of movement is parallel to the gradient. The paragraph also addresses the possibility of a negative rate of change, indicating a decrease, and how the magnitude of the gradient vector can be used to find the fastest rate of decrease.
🗺️ Gradient Vectors and the Geometry of Surfaces
The eighth paragraph explores the geometric implications of gradient vectors, particularly in relation to tangent planes and normal lines to surfaces. It explains how the gradient vector can be used to find the equation of a tangent plane to a surface at a given point, and how it can also be used to determine the direction of a normal line to the surface. The paragraph provides examples of how to calculate these geometric constructs using the gradient vector, emphasizing its utility in understanding the shape and orientation of surfaces in multivariable calculus.
🧭 Applications of Gradient Vectors in Surface Analysis
The final paragraph summarizes the various applications of gradient vectors discussed throughout the script. It highlights the gradient's role in finding the normal vector for tangent planes, the direction vector for normal lines, and the directions of the greatest rates of increase and decrease. The paragraph also touches on how the gradient is orthogonal to level curves and is instrumental in calculating directional derivatives. The summary underscores the gradient vector as a fundamental tool in multivariable calculus for analyzing surfaces and functions in higher dimensions.
Mindmap
Keywords
💡Directional Derivative
💡Gradient Vector
💡Partial Derivative
💡Unit Vector
💡Rate of Change
💡Flat Plate
💡Average Rate of Change
💡Instantaneous Rate of Change
💡Dot Product
💡Tangent Plane
Highlights
Introduction to the concept of directional derivatives and the gradient vector in the context of calculus.
Explanation of partial derivatives in relation to the rate of change in the direction of axes.
The process of finding a directional derivative in an arbitrary direction using unit vectors.
Demonstration of calculating the rate of change in temperature on a flat plate in a specific direction.
The definition and calculation of the directional derivative using the limit approach.
A theorem simplifying the computation of directional derivatives without using limit definitions.
Understanding the directional derivative in the context of unit vectors and partial derivatives.
Examples of finding directional derivatives for functions with given points and directions.
The significance of the gradient vector in representing the direction of greatest rate of change.
Application of the gradient in finding the maximum and minimum values of directional derivatives.
Use of the gradient to determine the direction of steepest ascent or descent on a surface.
Explanation of how the gradient is used to find the equation of a tangent plane to a surface.
The relationship between the gradient and the normal vector to a tangent plane.
Finding the direction of the steepest rate of temperature change using the gradient.
The application of the gradient in determining the direction of maximum increase or decrease on a hill surface.
Use of the gradient to find the points where the tangent plane is parallel to a given plane.
Summary of the gradient's various applications in calculus, including normal vectors, rate of change, and level curves.
Transcripts
Browse More Related Video
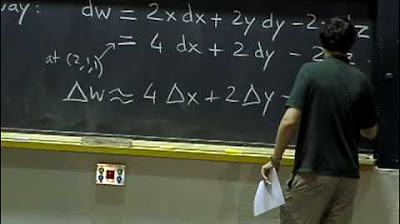
Lec 12: Gradient; directional derivative; tangent plane | MIT 18.02 Multivariable Calculus, Fall 07

Directional Derivatives | What's the slope in any direction?

Directional derivatives and slope

Why the gradient is the direction of steepest ascent

Directional Derivatives (Calculus 3)

Tensor Calculus 2: The Two Conflicting Definitions of the Gradient
5.0 / 5 (0 votes)
Thanks for rating: