What are derivatives in 3D? Intro to Partial Derivatives
TLDRThis video tutorial delves into the concept of partial derivatives in multivariable calculus. The instructor begins by illustrating the process of taking partial derivatives by fixing one variable and varying the other, effectively transforming a two-dimensional function into a one-dimensional one. The script explains the notation and method for calculating partial derivatives with respect to both x and y, emphasizing the geometric interpretation as the slope of the tangent line in the respective direction. The video also touches on the formal definition of partial derivatives using limits and provides a step-by-step guide on how to compute them, using an example function. It invites viewers to explore further in the series and encourages engagement in the comments section.
Takeaways
- 📚 The video is focused on explaining the concept of partial derivatives in the context of multivariable calculus.
- 📈 It starts by visualizing a function of two variables, f(x, y), and how to analyze it by fixing one variable and varying the other.
- 🔍 The script introduces the concept of a partial derivative by fixing the y-value and moving along the x-direction to find the slope of the tangent line at a point.
- 📐 It explains that the partial derivative with respect to x is found by treating y as a constant and taking the derivative as in single-variable calculus.
- 📉 Similarly, the partial derivative with respect to y is found by fixing x and varying y, treating x as a constant.
- 🔢 The formula for a partial derivative is presented as a fancy script 'D', pronounced as 'partial of F with respect to X', and written as ∂F/∂X.
- 📝 The process of finding a partial derivative involves evaluating the derivative of a one-dimensional function that results from fixing one variable.
- 📚 The script uses the long vertical bar to denote evaluation at a specific point, such as (x₀, y₀).
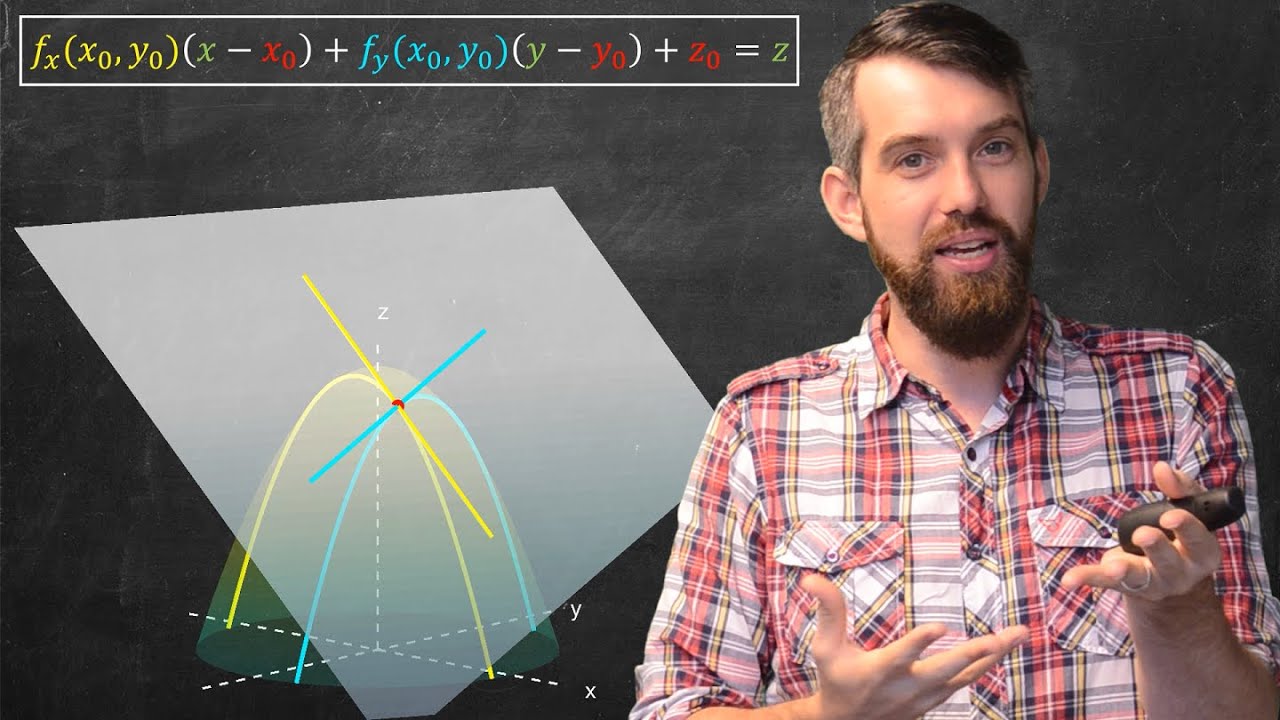
- 📉 It discusses the geometric interpretation of partial derivatives, explaining them as the slopes of the tangent lines in the respective directions of the variables.
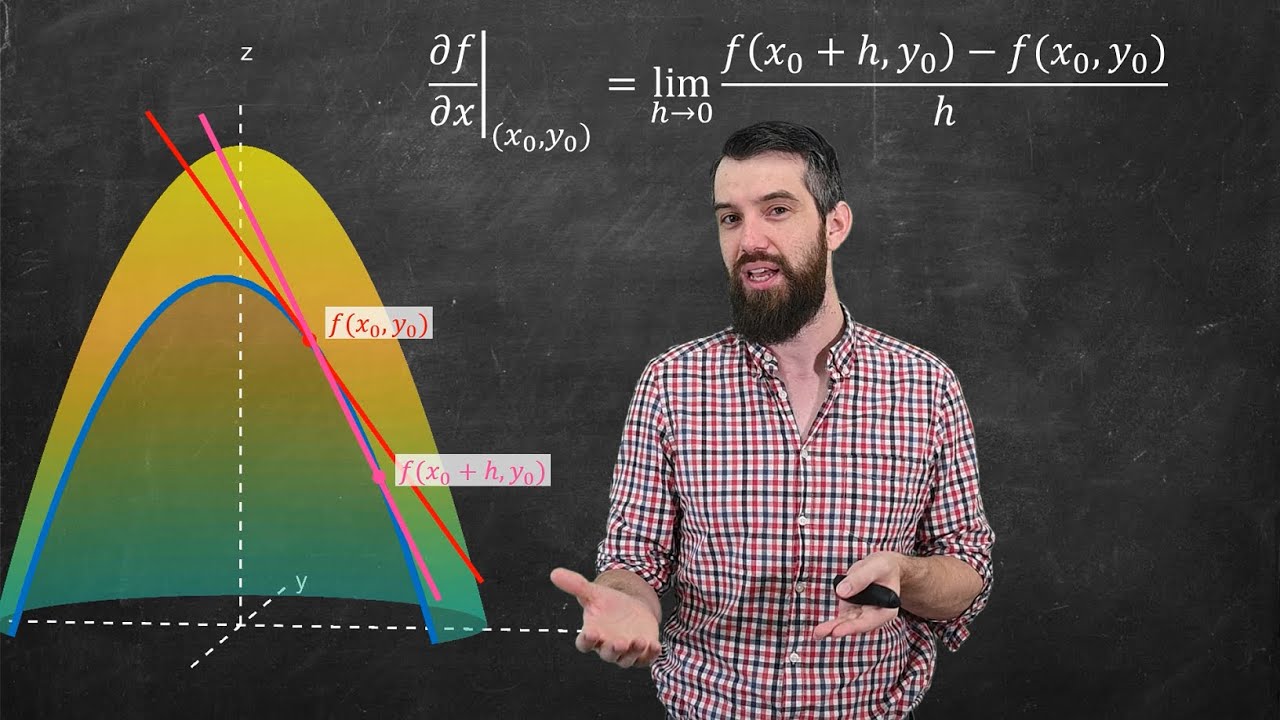
- 🔍 The method of finding partial derivatives is illustrated by considering the limit of the slopes of secant lines as they approach the tangent line.
- 📝 An example is provided to show how to compute partial derivatives for a function like 3x²y³ by treating the variable not being differentiated as a constant.
- 🔄 The video ends by posing a question about the slopes in other directions, suggesting further exploration of multivariable calculus concepts.
Q & A
What is a partial derivative?
-A partial derivative is a derivative of a function with more than one variable, where we differentiate with respect to one variable while treating all other variables as constants.
How does the process of taking a partial derivative relate to the process in single-variable calculus?
-The process of taking a partial derivative is similar to taking a derivative in single-variable calculus, except that when differentiating with respect to one variable, you treat all other variables as constants.
What does the notation ∂f/∂x represent?
-The notation ∂f/∂x represents the partial derivative of the function f with respect to the variable x, meaning the rate of change of the function as x changes, while all other variables are held constant.
Can you explain the geometric interpretation of a partial derivative?
-The geometric interpretation of a partial derivative is the slope of the tangent line to the surface represented by the function at a given point, in the direction of the variable with respect to which the derivative is taken.
What is the difference between a partial derivative with respect to x and a partial derivative with respect to y?
-The difference is the direction in which you are considering the change. A partial derivative with respect to x considers the slope in the x-direction, while a partial derivative with respect to y considers the slope in the y-direction, with all other variables held constant.
How do you find the partial derivative of a function like f(x, y) = 3x^2y^3?
-To find the partial derivative of f(x, y) = 3x^2y^3 with respect to x, treat y as a constant and differentiate normally as you would with a single-variable function, resulting in ∂f/∂x = 6x*y^3.
What is the significance of the vertical bar in the notation for partial derivatives?
-The vertical bar in the notation for partial derivatives, such as ∂f/∂x evaluated at a point, signifies that the derivative is to be evaluated at a specific point, often denoted as (x₀, y₀).
How does the concept of a tangent line in single-variable calculus extend to partial derivatives?
-The concept of a tangent line in single-variable calculus extends to partial derivatives by considering the slope of the tangent line to the surface at a point, in the direction of the variable with respect to which the derivative is taken.
What is the definition of a secant line in the context of partial derivatives?
-In the context of partial derivatives, a secant line is a line that connects two points on the surface of a function, and as the points get closer together, the slope of the secant line approximates the slope of the tangent line at a point.
How can you visualize the process of taking partial derivatives?
-You can visualize the process of taking partial derivatives by imagining a surface in three-dimensional space. When you take a partial derivative with respect to one variable, you are effectively 'slicing' the surface along a plane where the other variable is held constant, and then examining the slope of the resulting curve in that plane.
Outlines
📚 Introduction to Partial Derivatives
This paragraph introduces the concept of partial derivatives in the context of multivariable functions. The speaker begins by visualizing a function f(x, y) and explains the process of taking a partial derivative with respect to x by fixing the y value and moving along the x-axis. The idea is to transform a multivariable function into a one-variable function, allowing the use of standard calculus techniques to find the slope of the tangent line at a given point. The paragraph also introduces the notation for partial derivatives, emphasizing the difference from regular derivatives and the process of evaluating them at specific points.
🔍 Deep Dive into Partial Derivative Computation
The second paragraph delves deeper into the computation of partial derivatives, specifically with respect to x, by revisiting the definition of derivatives from first-year calculus. The process involves considering the slope of the tangent line as the limit of the slopes of secant lines, which is achieved by taking two points on the graph and examining the line that connects them. The speaker illustrates this with a point on the graph and introduces a second point by varying the x-value while keeping y constant. The formula for the partial derivative is then presented as the limit of the rise over run as the distance between the two points approaches zero. The paragraph also provides an example of how to compute a partial derivative for a function of the form 3x^2y^3, treating y as a constant when differentiating with respect to x. The summary concludes by highlighting the geometric interpretation of partial derivatives and hints at the complexity of derivatives in other directions, setting the stage for further exploration in future content.
Mindmap
Keywords
💡Partial Derivative
💡Graph
💡Tangent Line
💡Slope
💡Multivariable Function
💡Constrain
💡One-Dimensional Function
💡Derivative
💡Limit
💡Secant Line
💡Multivariable Calculus
Highlights
Introduction to taking partial derivatives with a focus on the graph of a function f(x, y).
Explaining the concept of fixing the Y value and moving only in the X direction to visualize the partial derivative.
Describing the transformation of a two-dimensional function into a one-dimensional function by constraining Y.
The geometric interpretation of a partial derivative as the slope of the tangent line to the constrained function.
The formula for a partial derivative and its notation, including the use of the del symbol.
How to compute partial derivatives by treating the other variable as a constant during differentiation.
The process of evaluating partial derivatives at a specific point by plugging in the fixed variable value.
Exploring the partial derivative with respect to Y, by fixing the X value and varying Y.
Visualizing the intersection of a plane with a function's graph to obtain a one-dimensional graph for partial differentiation.
The definition of partial derivatives in terms of limits, extending the concept from single-variable calculus.
A step-by-step guide on how to compute partial derivatives for a function like 3x^2y^3.
The geometric representation of partial derivatives as slopes in the X and Y directions on the function's surface.
Differentiating between the slopes of tangent lines when moving only along X or only along Y.
The concept of secant lines and their role in defining derivatives, including partial derivatives.
A detailed explanation of the limit process used to define the slope of the secant line as it approaches the tangent line.
Invitation for viewers to ask questions about the video in the comments section.
Encouragement for viewers to like the video to support the channel and its educational content.
Information on where to find a playlist of multivariable calculus videos for further learning.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: