Conditional and Absolute Convergence for Infinite Series
TLDRThis video discusses the concepts of absolute and conditional convergence in series. Absolute convergence occurs when the sum of the absolute values of the terms converges, allowing for the use of various convergence tests. Conditional convergence is when a series converges but not absolutely, often requiring the alternating series test. Examples include the alternating harmonic series and the sum of cosine of n over n squared, illustrating these concepts.
Takeaways
- 📚 Absolute convergence is determined by the sum of the absolute values of the series' terms.
- 🔍 If the series' absolute values converge, the series is absolutely convergent, allowing for the use of various convergence tests designed for positive terms.
- 🔄 Conditional convergence is identified when a series is not absolutely convergent but converges without considering the absolute values of its terms.
- 📉 The alternating series test is particularly useful for conditionally convergent series, as it checks for strict alternation and decreasing magnitude of terms.
- 🚫 A series that does not strictly alternate cannot be tested for convergence using the alternating series test.
- 📌 The harmonic series (1/n) is a classic example of a divergent series, which is used to illustrate the non-absolute convergence of certain series.
- 🔑 The alternating harmonic series (-1^n/n) is a well-known example of a conditionally convergent series, demonstrating the importance of alternating terms.
- 📐 The sum of cosine(n)/n^2 is an example of a series that converges absolutely, as shown by comparison to the convergent p-series with p=2.
- 📈 Absolute convergence implies that the series converges regardless of the order of its terms, which is a stronger condition than conditional convergence.
- 📝 Understanding the difference between absolute and conditional convergence is crucial for applying the correct tests and interpreting the behavior of infinite series.
- 🛠️ The script provides a practical approach to testing series for convergence by first checking for absolute convergence and then, if necessary, for conditional convergence.
Q & A
What is absolute convergence in the context of series?
-A series is absolutely convergent if the sum of the absolute values of its terms converges. This means that regardless of the order of terms, the series will converge because the sum of the magnitudes of the terms is finite.
Why is absolute convergence considered an 'easier problem'?
-Absolute convergence is considered easier because it allows for the use of convergence tests that require only positive terms, simplifying the analysis by avoiding the complications of alternating signs.
How does absolute convergence relate to the use of convergence tests?
-If a series is absolutely convergent, you can apply any convergence test that is designed for series with positive terms, broadening the range of tests that can be used to determine convergence.
What is conditional convergence and how does it differ from absolute convergence?
-Conditional convergence occurs when a series is not absolutely convergent (the sum of the absolute values of its terms diverges), but the series itself converges. This often involves the use of the alternating series test, which is applicable to series that alternate in sign.
Why is the alternating series test important for conditionally convergent series?
-The alternating series test is important because it is one of the few tests that can be used to determine the convergence of a series that includes negative terms, which is a characteristic of conditionally convergent series.
What is the alternating harmonic series and why is it a famous example of a conditionally convergent series?
-The alternating harmonic series is the sum of (-1)^n / n for n=1 to infinity. It is famous because it converges, but not absolutely, as the absolute values of its terms form the harmonic series, which is known to diverge. This makes it a clear example of a conditionally convergent series.
How can you determine if a series is absolutely convergent by using the sum of the cosine function?
-You can determine absolute convergence by taking the absolute value of each term in the series and checking if the resulting series converges. For the sum of the cosine function, you would compare the absolute value of the cosine terms over the square of n to a known convergent series, such as 1/n^2, to establish convergence by direct comparison.
What is the significance of the inequality in determining the absolute convergence of the cosine series?
-The inequality is used to bound the absolute value of the cosine terms, showing that they are less than or equal to 1/n^2. Since the series 1/n^2 is known to converge, the original series with cosine terms must also converge absolutely by direct comparison.
What does it mean for a series to converge by 'direct comparison'?
-Convergence by direct comparison means that the terms of the series in question are shown to be less than or equal to the terms of a known convergent series. If the comparison series converges, then the original series must also converge.
Why can't the alternating series test be used for the cosine series example given in the script?
-The alternating series test cannot be used for the cosine series example because the series does not strictly alternate in sign. The test requires that the terms of the series alternate between positive and negative values, which is not the case for the cosine function when n is an integer.
What is a p-series and how does it relate to the convergence of the series involving cosine terms?
-A p-series is a series of the form 1/n^p, where p is a positive real number. It relates to the convergence of the series involving cosine terms because the comparison series, 1/n^2, is a p-series with p=2. Since p>1, this p-series converges, indicating that the original series with cosine terms also converges absolutely.
Outlines
📚 Understanding Absolute and Conditional Convergence
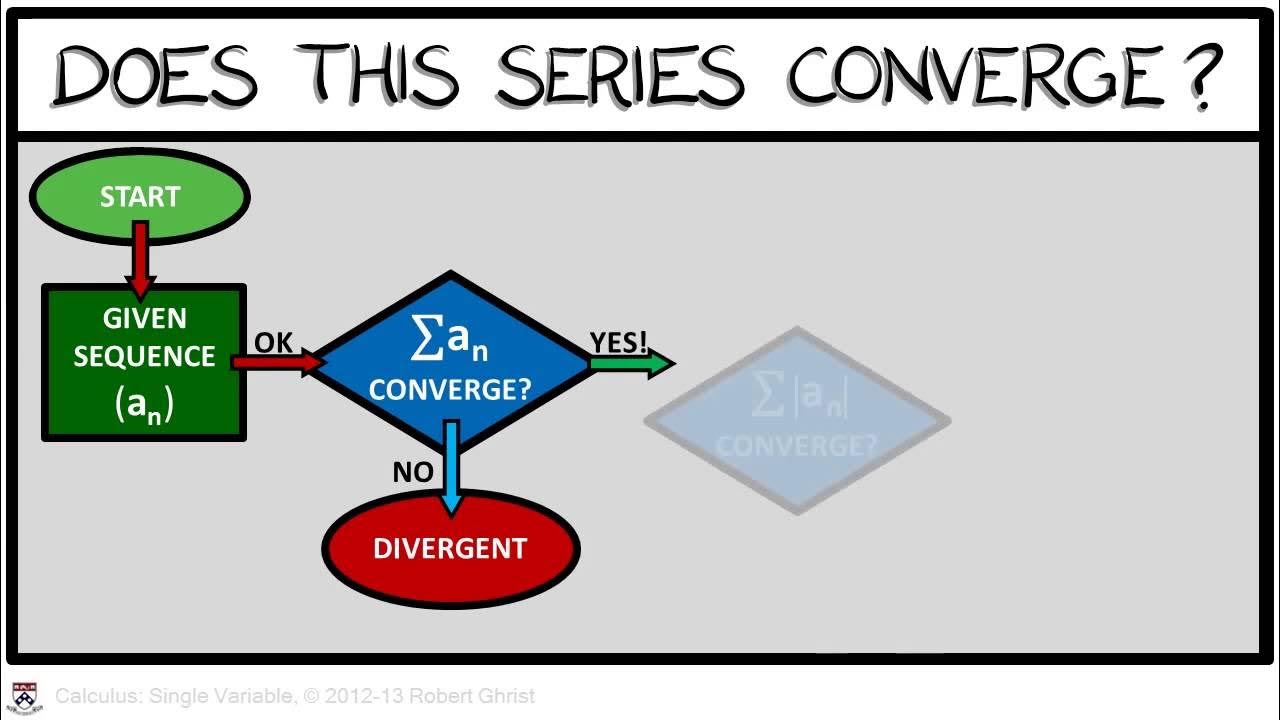
This paragraph introduces the concepts of absolute and conditional convergence in series. Absolute convergence occurs when the sum of the absolute values of the terms of a series converges. This simplifies the problem by eliminating the need to consider alternating signs. Conditional convergence, on the other hand, is when a series converges but not absolutely, meaning the sum of the absolute values of its terms diverges. The paragraph explains that absolute convergence allows for the use of various convergence tests that require only positive terms, making it a more straightforward approach. It also highlights the limitations of tests for alternating series, which require strict alternation. The paragraph sets the stage for exploring these concepts further through examples.
🔍 Analyzing Examples of Absolute and Conditional Convergence
This paragraph delves into the practical application of absolute and conditional convergence through examples. The first example is the series of negative one to the power of n over n. The speaker checks for absolute convergence by considering the sum of the absolute values of the terms, which results in the harmonic series, known to diverge. Consequently, the series is not absolutely convergent. However, upon applying the alternating series test, it is found to be conditionally convergent. The second example involves the series of cosine of n over n squared. The speaker demonstrates that this series converges absolutely by comparing it to the sum of one over n squared, which is known to converge. This comparison shows that the original series also converges, illustrating the importance of using additional tests like direct comparison to determine convergence. The paragraph concludes by emphasizing the significance of understanding absolute and conditional convergence in the study of series.
Mindmap
Keywords
💡Absolute Convergence
💡Conditional Convergence
💡Alternating Series Test
💡Harmonic Series
💡Convergence Tests
💡P-Series
💡Direct Comparison Test
💡Cosine Function
💡Trigonometric Functions
💡Inequality
Highlights
Introduction to the concept of conditional versus absolute convergence in series.
Definition of absolute convergence as the convergence of the sum of the absolute values of the series' terms.
Explanation of how taking the absolute value simplifies the problem by eliminating the need to consider alternating signs.
Advantage of absolute convergence in allowing the use of various convergence tests designed for positive terms only.
Conditional convergence as a fallback when a series is not absolutely convergent but converges without absolute values.
The necessity of the alternating series test for conditionally convergent series with alternating signs.
Illustration of the process to determine absolute convergence by checking the sum of the absolute values of the terms.
Example of the harmonic series and its divergence, indicating the non-absolute convergence of the series.
Application of the alternating series test to determine conditional convergence of the harmonic series.
The alternating harmonic series as a classic example of a conditionally convergent series.
Introduction of the second example involving the sum of cosine of n over n squared.
Explanation of why the alternating series test cannot be applied to the cosine example due to non-strict alternation.
Demonstration of proving absolute convergence by comparing the series to a known convergent series.
Use of the direct comparison test to establish the convergence of the cosine series by comparing it to the sum of 1/n^2.
Emphasis on the importance of additional tests like direct comparison when determining convergence.
Conclusion that absolute convergence guarantees the convergence of a series, as illustrated by the cosine example.
Encouragement for viewers to use the provided examples as a reference for understanding conditional and absolute convergence.
Transcripts
Browse More Related Video

Absolute and Conditional Convergence

AP Calculus BC Lesson 10.9

Conditional & absolute convergence | Series | AP Calculus BC | Khan Academy

Calculus BC – 10.9 Determining Absolute or Conditional Convergence
Calculus Chapter 5 Lecture 53 Absolute & Conditional

Alternating Series, Types of Convergence, and the Ratio Test
5.0 / 5 (0 votes)
Thanks for rating: