Tensor Calculus Lecture 14a: Non-hypersurfaces

MathTheBeautiful

12 Jul 201412:53

EducationalLearning

32 Likes 10 Comments

TLDRThe video script delves into the concept of principal curvatures, offering a geometric interpretation of mean and Gaussian curvatures. It discusses curves from both a one-dimensional and higher-dimensional perspective, emphasizing the shift in focus when considering curves in three-dimensional space as one-dimensional manifolds rather than hypersurfaces. The script highlights the differences in handling non-hypersurfaces, such as the absence of a single normal vector, and introduces the curvature normal tensor as a key concept for understanding curvature in non-hypersurface contexts.

Takeaways

📚 The video discusses the concept of principal curvatures, which provides a geometric interpretation to mean and Gaussian curvature.
🔍 The script explores curves from two perspectives: as one-dimensional objects and as embedded surfaces in higher-dimensional spaces.
📏 It mentions that the Frenet formulas are relevant when considering curves' one-dimensional nature and their properties such as binormal.
🌐 The video explains the difference between curves and hypersurfaces, emphasizing that a curve in 3D space is a one-dimensional manifold, not a hypersurface.
📉 The script points out that when dealing with embedded manifolds in spaces of different dimensions, certain concepts from differential geometry still apply, but some need to be redefined or reconsidered.
📝 The importance of using indices in tensor notation is highlighted, even for one-dimensional curves, to maintain the framework of tensor operations.
📐 The covariant basis and the metric tensor are still defined similarly for curves as they are for higher-dimensional surfaces.
🔄 The concept of the covariant derivative is fundamental and remains valid for curves, leading to the definition of curvature through the covariant derivative of the basis.
📊 The script introduces the curvature normal tensor 'B Alpha Beta', which is orthogonal to the surface and a key concept for non-hypersurfaces.
🚫 It clarifies that the mean curvature concept does not apply to non-hypersurfaces as there is no single normal vector, instead, there is a normal subspace.
🔑 The video concludes by emphasizing the generality of the discussed concepts, applicable to any dimensional manifold embedded in any dimensional ambient space.

Q & A

What is the main topic of discussion in the video script?
-The main topic of the video script is the concept of principal curvatures and how it provides a geometric interpretation to mean curvature and Gaussian curvature in the context of curves and surfaces.
Why is it important to discuss curves in the context of higher-dimensional spaces?
-Discussing curves in higher-dimensional spaces is important because it allows for a broader understanding of their properties and behaviors, which can be applied to more complex scenarios beyond the traditional three-dimensional space.
What is the difference between viewing curves as one-dimensional objects and viewing them as embedded surfaces?
-Viewing curves as one-dimensional objects focuses on their intrinsic properties like curvature and torsion, while viewing them as embedded surfaces in higher-dimensional spaces allows for the application of concepts from differential geometry that are typically used for surfaces.
What is a hypersurface and how does it differ from a curve in three-dimensional space?
-A hypersurface is a surface that only lacks one dimension compared to the ambient space. For example, a two-dimensional surface in a three-dimensional space is a hypersurface. A curve in three-dimensional space, however, is not a hypersurface; it is a one-dimensional manifold.
What is the significance of the covariant basis in the context of curves and surfaces?
-The covariant basis is significant because it provides a local coordinate system for the curves and surfaces, allowing for the definition of geometric properties such as the metric tensor and the covariant derivative, which are essential for analyzing curvature.
How does the concept of the normal change when dealing with non-hypersurfaces?
-For non-hypersurfaces, there is no single normal vector. Instead, there is a normal subspace, which is characterized by a set of vectors, not just one, as would be the case with a hypersurface.
What is the curvature normal tensor and how does it relate to the concept of mean curvature?
-The curvature normal tensor is a set of vectors that are orthogonal to the surface and are used to describe the curvature properties of the surface. It is analogous to the concept of mean curvature, but it is not an invariant and does not directly represent mean curvature when dealing with non-hypersurfaces.
Why is it necessary to use indices in the tensorial description of curves and surfaces?
-Indices are necessary in the tensorial description because they allow for the manipulation of covariant and contravariant components, which is essential for obtaining invariants and maintaining the tensorial machinery that describes the geometric properties of curves and surfaces.
How does the script suggest thinking about the one-dimensional nature of curves in the context of higher-dimensional manifolds?
-The script suggests considering the one-dimensional nature of curves as a special case within a more general discussion of higher-dimensional manifolds, using the same framework and structure for analysis, despite the dimensional differences.
What is the fundamental difference between the curvature properties of hypersurfaces and non-hypersurfaces?
-The fundamental difference is that for hypersurfaces, curvature properties can be described using a single normal vector and associated scalars (mean curvature). For non-hypersurfaces, there is no single normal vector, and the curvature properties are described by a set of vectors in a normal subspace, without a direct scalar multiple.
What is meant by the term 'curvature normal' in the context of non-hypersurfaces?
-In the context of non-hypersurfaces, 'curvature normal' refers to a vector that is orthogonal to the surface and is derived from the curvature normal tensor. It is an invariant that describes the curvature properties of the surface, but it does not have a direct scalar multiple as it would in the case of a hypersurface.

Outlines

00:00

📚 Introduction to Curves and Principal Curvatures

The script begins with a warm welcome back to the topic of curves, emphasizing the significance of principal curvatures in understanding mean and Gaussian curvatures. The speaker outlines two perspectives on curves: as one-dimensional objects with properties like curvature and binormal, and as embedded surfaces in higher-dimensional spaces. The script hints at the upcoming discussion on the one-dimensional nature of curves and their unique properties, contrasting them with hypersurfaces. The speaker invites the audience to reflect on the development of differential geometry principles for non-hypersurfaces and corrects a typo, promising to highlight the differences between hypersurfaces and other embedded manifolds.

05:00

🔍 Analyzing Curves in Higher-Dimensional Spaces

This paragraph delves into the analysis of curves as embedded surfaces in higher-dimensional spaces, maintaining the framework of indices and tensors from differential geometry. The speaker discusses the concepts of position vectors, covariant bases, and the metric tensor, which remain valid for curves despite their one-dimensional nature. The paragraph also touches on the shift tensor and covariant derivatives, highlighting their importance in understanding the geometry of curves. The speaker emphasizes the generality of these concepts across different dimensions and the transition from the Euclidean to the Riemannian space, where the geometric intuition is preserved algebraically.

10:01

🌐 The Concept of Curvature for Non-Hypersurfaces

The speaker explores the concept of curvature for non-hypersurfaces, noting the limitations of traditional definitions when applied to manifolds embedded in spaces of more than one dimension compared to the ambient space. The paragraph discusses the orthogonality of vectors to the surface and the transition from the normal vector in hypersurfaces to a normal subspace in non-hypersurfaces. The script introduces the 'curvature normal tensor' as a new concept to describe the curvature properties of non-hypersurfaces, which cannot be reduced to a single normal vector multiplied by scalars. The speaker also differentiates between mean curvature, applicable only to hypersurfaces, and the more general curvature normal tensor for non-hypersurfaces, inviting the audience to consider an example to illustrate these concepts.

Mindmap

Keywords

💡Principal Curvatures

Principal curvatures are the maximum and minimum curvatures at a point on a surface, which provide a geometric interpretation of the surface's shape. They are essential in understanding the concepts of mean curvature and Gaussian curvature. In the video, the speaker discusses how principal curvatures historically arose and their significance in the context of differential geometry.

💡Mean Curvature

Mean curvature is an average of the principal curvatures at a point on a surface, providing a measure of how curved the surface is. It is a key concept in differential geometry and is related to the integral of the principal curvatures. The video mentions that mean curvature is only applicable to hypersurfaces, which is a point of distinction when discussing non-hypersurfaces.

💡Gaussian Curvature

Gaussian curvature is the product of the principal curvatures and is a measure of the intrinsic curvature of a surface. It is a fundamental concept in differential geometry, indicating how the surface bends in two dimensions. The video script suggests that Gaussian curvature, like mean curvature, is deeply connected to the concept of principal curvatures.

💡Curves

In the context of the video, curves are one-dimensional objects that can be analyzed in various ways, such as considering their curvature or as embedded surfaces in higher-dimensional spaces. The script discusses how curves can be treated similarly to other surfaces when discussing properties like covariant derivatives and metric tensors.

💡Hypersurface

A hypersurface is a higher-dimensional analogue of a surface, lacking only one dimension compared to the space it is embedded in. For example, a two-dimensional surface in three-dimensional space is a hypersurface. The video script explains that when dealing with curves in three-dimensional space, they are no longer hypersurfaces, which changes the way certain geometric properties are considered.

💡Manifold

A manifold is a topological space that locally resembles Euclidean space near each point. In the script, the speaker discusses one-dimensional manifolds (curves) in three-dimensional space and two-dimensional manifolds in four-dimensional space, emphasizing that the latter are not hypersurfaces.

💡Covariant Basis

A covariant basis is a set of tangent vectors to a surface at a point, which provides a local coordinate system. The video script mentions that the concept of the covariant basis survives in the context of non-hypersurfaces, and it is used to define the metric tensor and perform covariant differentiation.

💡Metric Tensor

The metric tensor is a mathematical object that provides an inner product in the tangent space of a surface. It is used to measure distances and angles on the surface. In the video, the speaker explains that the concept of the metric tensor is applicable to curves and surfaces, including non-hypersurfaces.

💡Covariant Derivative

The covariant derivative is a way to take derivatives of vector fields and other tensors on a surface or manifold, taking into account the curvature of the space. The video script discusses how this concept is fundamental in differential geometry and remains valid for non-hypersurfaces.

💡Christoffel Symbols

Christoffel symbols are coefficients that express the covariant derivative in terms of the metric tensor and are used to describe the curvature of a manifold. The video script implies that while the definition of Christoffel symbols may vary with the dimensionality of the manifold, their properties remain consistent.

💡Curvature Normal Tensor

The curvature normal tensor, denoted as B in the script, is a set of vectors orthogonal to the surface. The video explains that for non-hypersurfaces, this tensor cannot be simply described as a scalar multiple of the normal vector, as there is no single normal vector, but rather a normal subspace.

Highlights

Introduction to the concept of principal curvatures and their geometric interpretation of mean and Gaussian curvature.

Exploration of curves from two perspectives: one-dimensional objects and embedded surfaces in higher-dimensional spaces.

Discussion on the Frenet formulas and their application to the curvature of curves when viewed as one-dimensional objects.

Clarification that curves in three-dimensional space are one-dimensional manifolds, not hypersurfaces.

Introduction of the concept of a hypersurface and its distinction from a curve in three-dimensional space.

Explanation of the differences in properties and formulas when dealing with embedded manifolds in spaces of different dimensions.

Highlighting the importance of indices in tensor notation, even for one-dimensional curves.

Discussion on the covariant basis and its role in defining the metric tensor for curves and surfaces.

Introduction of the shift tensor and its survival in the context of curves embedded in higher-dimensional spaces.

Explanation of the covariant derivative and its significance in the analysis of curvature.

Discussion on the Christoffel symbols and their properties in the context of non-hypersurfaces.

Introduction of the curvature normal tensor and its orthogonality to the surface.

Clarification on the difference between the curvature normal tensor and the concept of mean curvature, especially for non-hypersurfaces.

Discussion on the invariant properties of the curvature normal tensor and its generalization to any dimensional manifold.

Highlighting the importance of the curvature normal tensor as a standalone object when dealing with non-hypersurfaces.

Final thoughts on the generalizability of tensor machinery to any dimensional ambient space and its implications for the study of curves and surfaces.

Transcripts

Browse More Related Video

Tensor Calculus Lecture 14e: Non-hypersurfaces - Relationship Among Curvature Tensors 2

Tensor Calculus Lecture 14c: Non-hypersurfaces - Relationship Among The Shift Tensors

Tensor Calculus Lecture 14f: Principal Curvatures

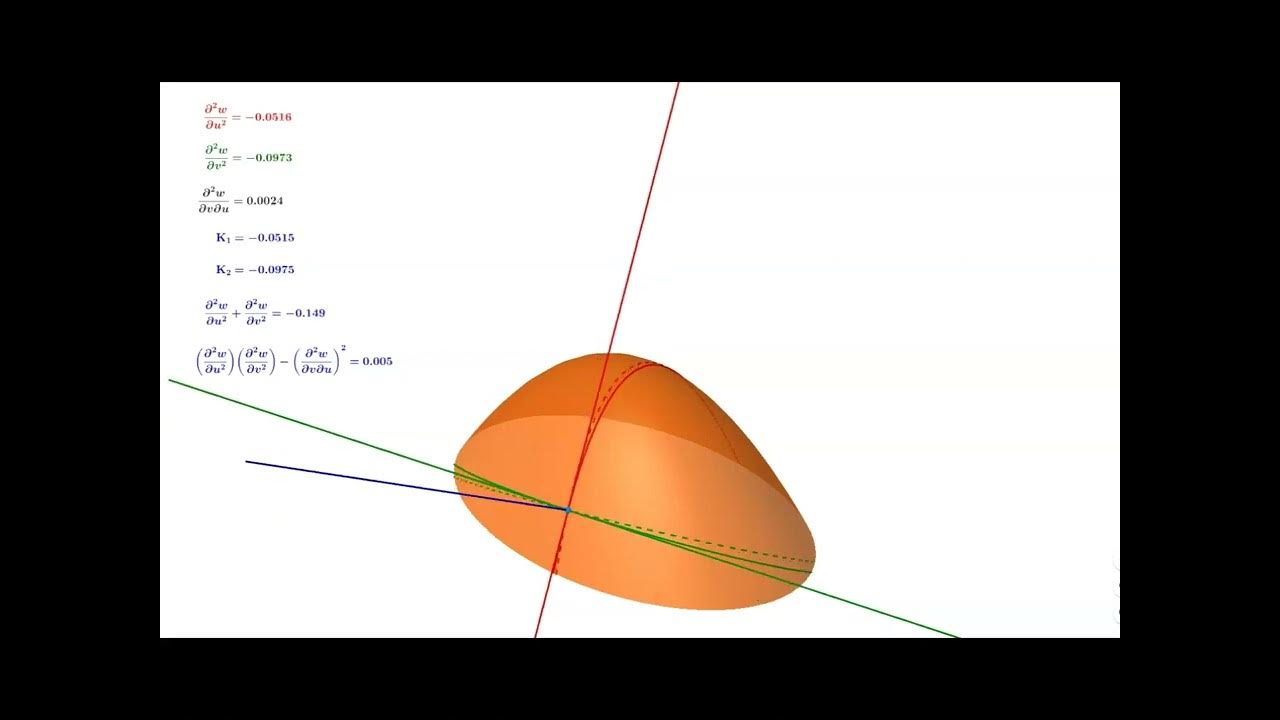
Video 78 - Gaussian Curvature

Tensor Calculus Lecture 8e: The Riemann Christoffel Tensor & Gauss's Remarkable Theorem

Tensor Calculus Lecture 14b: Examples of Curves in 3D

Tensor Calculus Lecture 14a: Non-hypersurfaces

Takeaways

Q & A

What is the main topic of discussion in the video script?

Why is it important to discuss curves in the context of higher-dimensional spaces?

What is the difference between viewing curves as one-dimensional objects and viewing them as embedded surfaces?

What is a hypersurface and how does it differ from a curve in three-dimensional space?

What is the significance of the covariant basis in the context of curves and surfaces?

How does the concept of the normal change when dealing with non-hypersurfaces?

What is the curvature normal tensor and how does it relate to the concept of mean curvature?

Why is it necessary to use indices in the tensorial description of curves and surfaces?

How does the script suggest thinking about the one-dimensional nature of curves in the context of higher-dimensional manifolds?

What is the fundamental difference between the curvature properties of hypersurfaces and non-hypersurfaces?

What is meant by the term 'curvature normal' in the context of non-hypersurfaces?