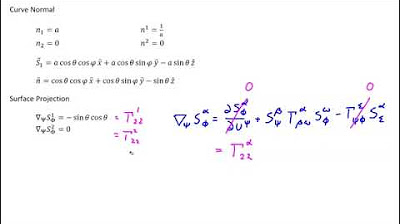Tensor Calculus Lecture 14e: Non-hypersurfaces - Relationship Among Curvature Tensors 2
TLDRThis video script delves into the concept of hypersurfaces, focusing on the relationship between a one-dimensional curve embedded in a two-dimensional surface within a three-dimensional space. It introduces the curvature normal tensor and explores its properties, leading to an algebraic approach to understand mean curvature. The script emphasizes the power of tensor framework in combining analytical and geometric methods, culminating in a boxed expression that relates mean curvatures in different dimensions, offering a deeper insight into the geometric properties of embedded curves and surfaces.
Takeaways
- 📚 The script discusses a mathematical concept involving hypersurfaces and their properties within an ambient space, focusing on the relationship between a curve, a surface, and the three-dimensional space they are embedded in.
- 📐 The script introduces the idea of normals to hypersurfaces, explaining how a curve within a surface has a well-defined normal, denoted by 'n', which can point in one of two directions.
- 🔍 The concept of the curvature normal tensor is introduced, which is related to the curvature of the curve embedded in the surface, and is represented with unfamiliar symbols to emphasize the new context of the discussion.
- 📈 The script explains the algebraic manipulation of tensors to derive the mean curvature of a curve with respect to the surface, highlighting the importance of the tensor framework in simplifying complex geometric concepts.
- 🧠 The speaker emphasizes the effectiveness of using geometry to set up algebraic problems and then proceeding with analytical methods, suggesting that this is a powerful approach in understanding complex mathematical relationships.
- 📉 The script introduces the notion of geodesic curvature, which will be discussed in more detail in the context of moving surfaces, indicating that it is a minimization problem related to shape optimization.
- 🔢 The script provides a detailed algebraic expression for the mean curvature of a curve within a surface, breaking it down into components that can be visualized and understood in the context of the three-dimensional space.
- 📝 The importance of the shift tensor is highlighted, showing how it is used to translate surface components to ambient coordinates, which is crucial for understanding the relationship between different hypersurfaces.
- 📝 The script presents a boxed expression that relates mean curvatures, indicating a significant relationship between the curvature of the curve within the surface and the overall space.
- 🤔 The script encourages the viewer to pause and reflect on the concepts discussed, particularly the projection formula and its application to the current context, suggesting that a deeper understanding can be achieved through careful consideration of these relationships.
- 📚 The final takeaway is the encouragement to think about the relationship between different spaces and how the components of the mean curvature vector point in different directions, normal to the curve and the surface.
Q & A
What is a hypersurface in the context of the script?
-In the script, a hypersurface refers to a higher-dimensional analogue of a surface in a space of one more dimension. It is used to describe a curve within a surface, which is itself within a three-dimensional space.
Why are lowercase letters used for certain normals in the script?
-Lowercase letters are used to denote the normal of the curve with respect to the surface it is embedded in, as opposed to the uppercase normal which is used for the surface's normal in the ambient space.
What is the significance of the normal vector 'n' in the script?
-The normal vector 'n' is significant as it represents the direction perpendicular to the curve within the surface. It is used to define the curvature normal tensor and helps in understanding the geometric properties of the curve.
What is meant by the curvature normal tensor in the context of the script?
-The curvature normal tensor in the script refers to a mathematical object that describes the curvature of the curve embedded in the surface, taking into account the normal vectors and the curvature tensor of the higher-dimensional embedding.
What is the role of the shift tensor in the script?
-The shift tensor is used to project the components of the normal vector from the surface to the ambient space, effectively translating surface components to the three-dimensional space.
How is the mean curvature of the curve within the surface represented in the script?
-The mean curvature of the curve within the surface is represented by the term 'b_i_phi phi' in the script, which is derived from the contraction of the curvature tensor with the normal vectors.
What is the significance of the term 'geodesic curvature' mentioned in the script?
-Geodesic curvature is another term for the mean curvature of a curve within a surface, which is particularly relevant when discussing moving surfaces or shape optimization problems.
What is the importance of the projection formula in the script?
-The projection formula is important as it allows for the translation of the normal vector components from the surface to the ambient space, which is essential for understanding the geometric relationships in higher dimensions.
How does the script suggest using geometry to set up algebraic problems?
-The script suggests using geometric intuition to set up the algebraic problem, then proceeding analytically with tensor framework to dictate the next steps, rather than relying solely on geometric intuition.
What is the relationship between the curvature tensors and mean curvatures as described in the script?
-The script describes a boxed expression that relates the mean curvatures of the curve within the surface and the surface within the ambient space, highlighting the connection between different curvature tensors.
What does the script suggest about the direction of the terms in the normal space?
-The script suggests that the direction of the terms in the normal space can be thought of as having components both tangential and normal to the surface, with the normal component being particularly interesting for further analysis.
Outlines
📐 Hypersurfaces and Curvature Basics
The paragraph introduces the concept of hypersurfaces and their relationship to ambient space, using a three-dimensional space as an example with a two-dimensional surface and a one-dimensional curve embedded within. The author explains the use of normals and the curvature normal tensor, emphasizing the importance of lowercase letters for denoting different normals. The paragraph also introduces the curvature tensor for the hyperembedding and its components, providing a foundational understanding of the concepts that will be built upon in subsequent discussions.
🔍 Analytical Approach to Geometric Concepts
This paragraph delves into the analytical method of understanding geometric concepts, such as the curvature tensor for a curve embedded in a surface. The author discusses the process of algebraic manipulation and tensor framework to derive meaningful results without relying on geometric intuition. The paragraph also introduces the concept of mean curvature and its representation using tensor notation, highlighting the power of the tensor framework in combining analytical and geometric methods effectively.
🌐 Shift Tensors and Curvature Relationships
The focus of this paragraph is on the shift tensors and their role in the projection formula within the context of curvature. The author explains how these tensors are contracted and how they relate to the curvature normal. The paragraph also introduces a boxed expression that relates mean curvatures in different spaces, providing a deeper understanding of the relationship between curvature tensors and the mean curvature of the curve within the surface.
🧭 Geodesic Curvature and Normal Space Analysis
The final paragraph discusses the concept of geodesic curvature and its relation to the mean curvature of a curve within a surface. The author suggests thinking about the components of the curvature in both the tangential and normal directions to the curve. The paragraph concludes with an exploration of the implications of dotting the entire relationship with the normal, hinting at further analysis in the normal space that will be discussed in subsequent content.
Mindmap
Keywords
💡Hypersurface
💡Normal
💡Curvature Tensor
💡Mean Curvature
💡Shift Tensor
💡Geodesic Curvature
💡Ambient Space
💡Tangent Plane
💡Algebraic Framework
💡Tensor Calculus
💡Geometric Intuition
Highlights
Introduction of a general relationship derived from previous work, focusing on hypersurfaces and their geometric properties.
Assumption of all embeddings as hypersurfaces, simplifying the analysis of geometric relationships in higher dimensions.
Visualization of a one-dimensional curve in a two-dimensional surface within a three-dimensional space for ease of understanding.
Introduction of the normal vector and its significance in defining hypersurfaces within an ambient space.
Explanation of the curvature normal tensor and its role in the context of embedded hypersurfaces.
Differentiation between lowercase and uppercase letters in tensor notation to denote different normals in the geometric context.
Algebraic simplification of the curvature tensor for the curve embedded in the surface.
Discussion on the importance of the shift tensor in translating surface components to ambient coordinates.
Raising of the Greek index and contraction to derive the mean curvature of the curve with respect to the surface.
Emphasis on the analytical approach over geometric intuition in solving tensor-based problems.
Introduction of the concept of geodesics and its relation to moving surfaces and shape optimization problems.
Explanation of the mean curvature as a primary concept, with geodesic curvature as an alternative term in specific contexts.
Boxing of a key relationship that connects mean curvatures and curvature normals in different dimensions.
Interpretation of the boxed expression as a connection between different spaces and directions.
Final discussion on the components of the mean curvature vector in both tangential and normal directions to the curve and surface.
Encouragement for the audience to pause and reflect on the tensor framework and its application to the problem at hand.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: