Tensor Calculus Lecture 14b: Examples of Curves in 3D
TLDRThis script delves into the concept of curvature normals in tensor calculus, contrasting the properties of a spiral and a sine curve. It emphasizes the importance of choosing a coordinate system and the invariant nature of curvature normals, which are unaffected by the parametrization of the curve. The discussion highlights the difference between hypersurfaces, where normals can vary in sign, and non-hypersurfaces, where the curvature normal is unambiguously defined. The script encourages the exploration of tensor calculus to understand these geometric invariants fully.
Takeaways
- 📚 The script discusses the concept of curvature normal in the context of tensor calculus, emphasizing the importance of choosing a coordinate system for detailed analysis.
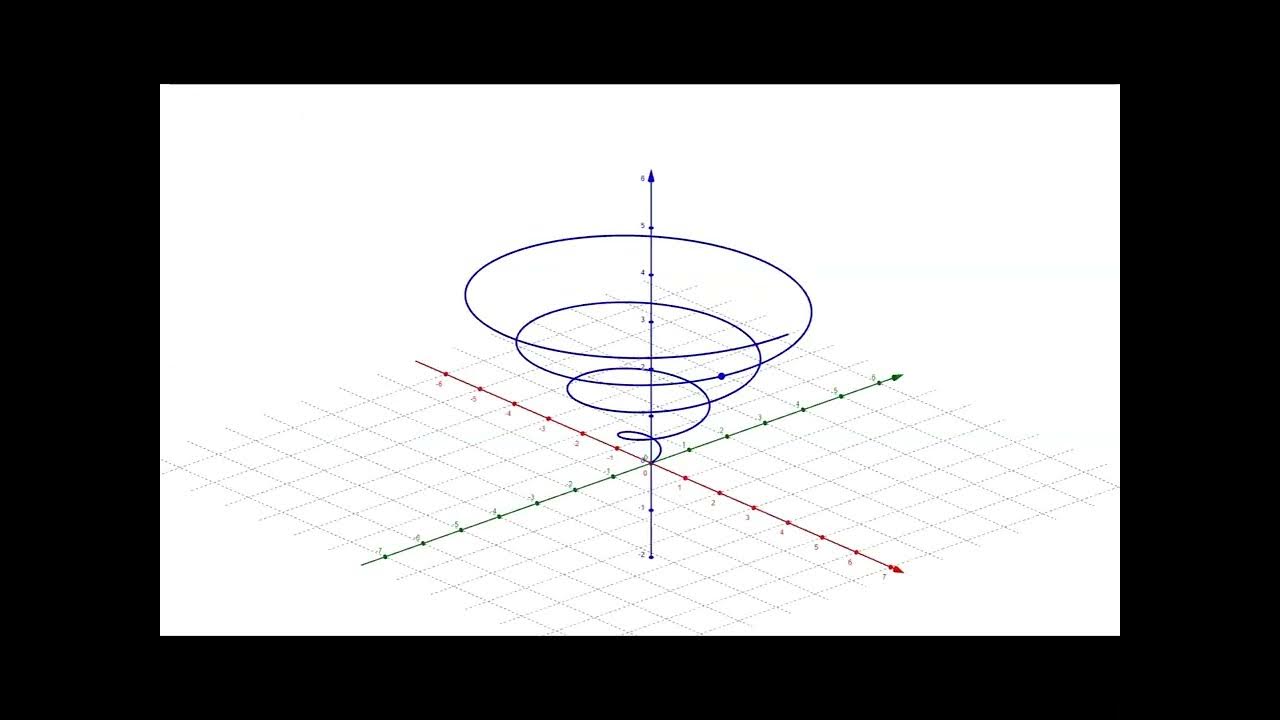
- 🌀 It uses the example of a spiral to illustrate the concept, explaining how to visualize the curvature normal as an invariant vector pointing towards the axis of the spiral.
- 📏 The script clarifies that the curvature normal is independent of the parametrization of the curve, as long as it is proper and does not stop and resume inconsistently.
- 🔍 When discussing the spiral, the script suggests that the curvature normal will be horizontal and its length could be related to the inverse of the spiral's radius.
- 🚫 The script highlights that there is no arbitrariness in the choice of the curvature normal for a spiral, unlike in hypersurfaces where the normal can be chosen in different directions.
- 📉 The script then moves on to discuss a sine curve, explaining how the curvature normal can be visualized and how it changes direction as the curve oscillates.
- 📐 At points of inflection on the sine curve, the script notes that the curvature normal is zero, and thus the principal normal is undefined, while the curvature normal itself is perfectly well-defined.
- 📈 The script makes a comparison between considering the sine curve in three-dimensional space and as a hypersurface within a plane, noting the differences in how the curvature normal and mean curvature are defined.
- 🔄 When the sine curve is considered as a hypersurface, the script explains that the normal to the plane is arbitrary with respect to sign, and a normal field can be defined.
- 🔗 The script connects the concepts by stating that for a curve that can be considered both a hypersurface and not a hypersurface, both curvature normal and mean curvature can be defined, and they are related through an explicit expression.
- 🔑 The final takeaway is the importance of tensor calculus in capturing the rate and direction of curving in an invariant way, regardless of the coordinate system chosen for the analysis.
Q & A
What is the primary goal of discussing the spiral and sine curve examples in the context of tensor calculus?
-The primary goal is to give a general idea of how to use tensor calculus to analyze the curvature of these curves and to save the detailed calculations as an exercise for the learner, emphasizing the importance of choosing a coordinate system and using tensor calculus to arrive at an invariant answer.
Why is choosing a coordinate system important in the context of tensor calculus?
-Choosing a coordinate system is important because it allows for the application of tensor calculus machinery to analyze geometric objects invariantly, meaning the results are independent of the chosen coordinate system, which is a fundamental aspect of tensor calculus.
What does the script suggest as a coordinate system for the spiral example?
-The script suggests a uniform coordinate system starting at zero for the spiral example, without specifying it as arc length, to maintain the spirit of tensor calculus and to facilitate the visualization of the curvature normal.
What is the curvature normal in the context of the spiral example?
-The curvature normal is an invariant vector that points inward towards the axis of the spiral and is derived from the second derivative of the curve's equation. It represents both the rate and direction of the curve's bending.
How does the curvature normal relate to the principal normal for a one-dimensional curve?
-The curvature normal, when considered as a unit vector, is referred to as the principal normal. It is a special normal direction that corresponds to the acceleration of a particle moving along the curve and is invariant under proper parametrization.
What is the significance of the curvature normal being invariant regardless of the parametrization of the curve?
-The invariance of the curvature normal means that it captures the intrinsic geometric property of the curve's bending, independent of how the curve is parameterized, as long as the parametrization is proper and continuous.
What is the difference between discussing the sine curve as a three-dimensional object and as a hypersurface within a plane?
-When discussing the sine curve as a three-dimensional object, the curvature normal is considered without regard to any plane it might lie in. As a hypersurface within a plane, the sine curve has a normal to the plane, which introduces an element of arbitrariness in the choice of normal direction and allows for the definition of mean curvature.
Why is the curvature normal undefined at the inflection points of the sine curve?
-At inflection points, the curvature normal is undefined because the second derivative, which determines the direction of the curvature normal, is zero, indicating no change in the direction of the curve at those points.
What is the relationship between the curvature normal and the mean curvature for a curve that lies in a plane?
-For a curve in a plane, the curvature normal can be related to the mean curvature by taking the dot product of the curvature normal vector with the hypersurface normal. This relationship provides an explicit expression of mean curvature in terms of the curvature normal.
How does the script connect the concepts of curvature normal and mean curvature for both hypersurfaces and non-hypersurfaces?
-The script connects these concepts by showing that for a curve that can be considered both as a hypersurface and not a hypersurface, one can define both the curvature normal and the mean curvature. It also demonstrates that the curvature normal equals the mean curvature dotted with the hypersurface normal, highlighting the relationship between these two quantities.
Outlines
📚 Introduction to Tensor Calculus and Curves
The script begins with an introduction to tensor calculus, focusing on its application to geometric objects such as spirals and sine curves. The speaker aims to provide a conceptual understanding rather than a detailed worked example, encouraging the audience to explore the details as an exercise. The importance of selecting an appropriate coordinate system is emphasized, with a Cartesian coordinate system suggested for discussing invariant geometric properties. The concept of the curvature normal, an invariant vector, is introduced as a key visual element for understanding the curvature of one-dimensional surfaces like spirals.
🌀 Analyzing the Curvature Normal of a Spiral
This paragraph delves into the specifics of analyzing the curvature normal of a spiral. The speaker discusses the process of selecting a uniform coordinate system and visualizing the covariant basis, or the tangent vector, which represents the velocity vector as the point moves along the spiral. The inclination of the spiral is described as constant, leading to a horizontal vector when the index is raised. The curvature normal is then defined as an invariant that points inward towards the axis of the spiral, with its length suggested to be inversely proportional to the spiral's radius. The paragraph also touches on the invariance of the curvature normal with respect to the direction of parametrization, highlighting the absence of arbitrariness in its definition.
🔄 Curvature Normal of a Sine Curve in 3D Space
The script continues with an exploration of the curvature normal of a sine curve in three-dimensional space, initially ignoring the fact that it lies in a plane. The curvature normal is described as a vector that points inwards, with its magnitude varying along the curve, being highest at points of maximum curvature. The principal normal is introduced as a unit vector in the same direction as the curvature normal, but it is noted that it is not defined at points of inflection. The paragraph also discusses the invariant nature of the curvature normal, which captures both the rate and direction of curving, and its independence from the choice of coordinates or parametrization.
📉 Connection Between Curvature Normal and Hypersurface Normal
The final paragraph connects the concepts discussed in the previous sections by considering the sine curve as both a hypersurface and a non-hypersurface. The speaker explains that when the sine curve is considered as a hypersurface within a plane, it has a normal vector, which can be chosen arbitrarily in sign. This allows for the definition of a normal field and mean curvature. The relationship between the curvature normal and the hypersurface normal is established, with the curvature normal being equal to the product of the mean curvature and the hypersurface normal. The paragraph concludes by highlighting the utility of this relationship in understanding principal curvatures in future lectures.
Mindmap
Keywords
💡Tensor Calculus
💡Curvature Normal
💡Spirals
💡Sine Curve
💡Principal Normal
💡Coordinate System
💡Invariant
💡Hypersurface
💡Mean Curvature
💡Parametrization
💡Inflection Point
Highlights
Introduction to the concept of tensor calculus in analyzing the curvature of geometric objects.
Discussion of the importance of choosing a coordinate system in tensor calculus for invariant answers.
The use of a uniform coordinate system for convenience in visualizing the curvature normal vector.
Explanation of the covariant basis and its relation to the velocity vector of a moving point on a curve.
Illustration of the spiral's constant inclination and its impact on the direction of the curvature normal.
Clarification on the invariance of the curvature normal vector in one-dimensional surfaces.
The role of raising the index in tensor calculus to achieve an invariant length.
The invariant nature of the curvature normal vector and its horizontal orientation in the case of a spiral.
The absence of arbitrariness in the curvature normal vector for a spiral due to the lack of a choice of normal.
The invariance of the curvature normal vector regardless of the parametrization of the curve.
Introduction to the sine curve as an example of a different geometric object for curvature analysis.
The unique curvature properties of a sine curve and the definition of its curvature normal.
The distinction between the curvature normal and the principal normal in the context of a sine curve.
The impact of inflection points on the definition of the principal normal in a sine curve.
The invariant nature of the curvature normal vector in capturing the rate and direction of curving.
The relationship between the curvature normal and the hypersurface normal in the context of a sine curve lying in a plane.
The comparison between the curvature normal and the mean curvature tensor for a hypersurface.
The explicit expression of mean curvature in terms of the curvature normal for a curve in a plane.
The connection between the curvature normal and the mean curvature for both hypersurfaces and non-hypersurfaces.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: