Video 78 - Gaussian Curvature
TLDRThis video script introduces Gaussian curvature, a fundamental concept in tensor calculus developed by Carl Friedrich Gauss, which measures the curvature of a 2D surface. The script uses an elliptic paraboloid to illustrate the concept, explaining how to construct tangent planes and basis vectors to find the maximum and minimum curvatures, known as principal curvatures. It further explains how to derive invariant quantities like mean curvature and Gaussian curvature, which are intrinsic properties of the surface, unaffected by the normal direction. The video also touches on how these concepts apply to different surfaces, such as paraboloids and hyperbolic paraboloids, and hints at the connection to tensor calculus in the subsequent video.
Takeaways
- 📚 The video introduces Gaussian curvature, a fundamental concept in tensor calculus that quantifies the curvature of a two-dimensional surface.
- 📐 The elliptic paraboloid is used as an example to illustrate the concept of Gaussian curvature, showing its cross-sections as ellipses and parabolas.
- 🔍 Carl Friedrich Gauss developed Gaussian curvature in the early 19th century, and the video demonstrates how to construct tangent planes and basis vectors on a surface.
- 📉 The curvature of a curve on the surface is found by taking the second derivative of the function representing the curve in a two-dimensional space.
- 🔄 The process of finding the maximum and minimum curvature (principal curvatures) involves rotating a line in the tangent plane and observing changes in curvature values.
- 📏 Principal curvatures are denoted by the Greek letters kappa (κ), with κ1 being the maximum curvature and κ2 the minimum curvature at a given point on the surface.
- 🧭 The principal curvatures are found when the constructed axes (u and v) are perpendicular to each other, and the mixed second derivative vanishes.
- 📈 Gauss discovered invariants in the process, such as the sum and the product of the principal curvatures, which lead to the definitions of mean curvature and Gaussian curvature.
- 📊 Mean curvature is an invariant value, calculated as the average of the principal curvatures, while Gaussian curvature is the product of the principal curvatures.
- 🔃 The direction of the normal vector affects the sign of the principal curvatures and mean curvature, but not the Gaussian curvature, which is an intrinsic property of the surface.
- 🔍 Different surfaces, such as a simple paraboloid, hyperbolic paraboloid, and others, demonstrate various curvature properties, including zero Gaussian curvature for surfaces that can be flattened without distortion.
Q & A
What is Gaussian curvature?
-Gaussian curvature is a measure of the curvature of a two-dimensional surface, developed by Carl Friedrich Gauss in the early 19th century. It is an intrinsic property of the surface that quantifies how much the surface deviates from being a plane.
What is an elliptic paraboloid and how does it relate to Gaussian curvature?
-An elliptic paraboloid is a surface that has an elliptical cross-section when viewed from the top and parabolas when viewed from the front or side. It is used in the script to illustrate the concept of Gaussian curvature by examining the curvature at different points on the surface.
What are the surface covariant basis vectors and how do they relate to the tangent plane?
-The surface covariant basis vectors, denoted as s1 and s2 in the script, are vectors that lie in the tangent plane to the surface at a given point. They help in defining the local coordinate system on the surface and are essential for calculating Gaussian curvature.
What is the significance of the normal vector in the context of Gaussian curvature?
-The normal vector, represented as n̂ in the script, is a unit vector perpendicular to the tangent plane of the surface at a given point. It is crucial for defining the orientation of the surface and plays a role in determining the principal curvatures.
What are the principal curvatures and how are they found?
-Principal curvatures, denoted as kappa1 and kappa2 in the script, are the maximum and minimum curvatures at a point on a surface. They are found by constructing intersecting lines through the point and rotating them until the mixed second partial derivative vanishes, indicating the axes of maximum and minimum curvature.
How is the curvature of an intersected curve calculated?
-The curvature of an intersected curve is calculated by taking the second derivative of the function representing the curve with respect to the coordinate along the curve. This second derivative gives the curvature at a specific point on the curve.
What is the mean curvature and how is it different from Gaussian curvature?
-The mean curvature is an invariant quantity that represents the average of the two principal curvatures. It is different from Gaussian curvature, which is the product of the two principal curvatures. While mean curvature gives the average curvature, Gaussian curvature provides a measure of the intrinsic curvature of the surface.
Why is Gaussian curvature considered an intrinsic property of a surface?
-Gaussian curvature is considered an intrinsic property of a surface because it is independent of the choice of coordinates or the orientation of the normal vector. It is a measure of the curvature that is inherent to the surface itself, regardless of how it is embedded in space.
How does the sign of the principal curvatures affect the Gaussian curvature?
-The sign of the principal curvatures determines the nature of the Gaussian curvature. If both principal curvatures have the same sign, the Gaussian curvature is positive, indicating that the surface curves in the same direction in all directions from the point. If the principal curvatures have opposite signs, the Gaussian curvature is negative, indicating that the surface curves in opposite directions.
What is the relationship between the sum and product of the principal curvatures and the mean and Gaussian curvatures?
-The sum of the principal curvatures (kappa1 + kappa2) gives the mean curvature, while the product of the principal curvatures (kappa1 * kappa2) gives the Gaussian curvature. These relationships show how the average and intrinsic curvatures of the surface are derived from the maximum and minimum curvatures at a point.
Can a surface have zero Gaussian curvature?
-Yes, a surface can have zero Gaussian curvature. This occurs when the product of the principal curvatures is zero, which can happen if one of the principal curvatures is zero. Such surfaces can be flattened out into a plane without stretching or deforming, indicating that they are intrinsically flat despite appearing curved.
Outlines
📐 Introduction to Gaussian Curvature
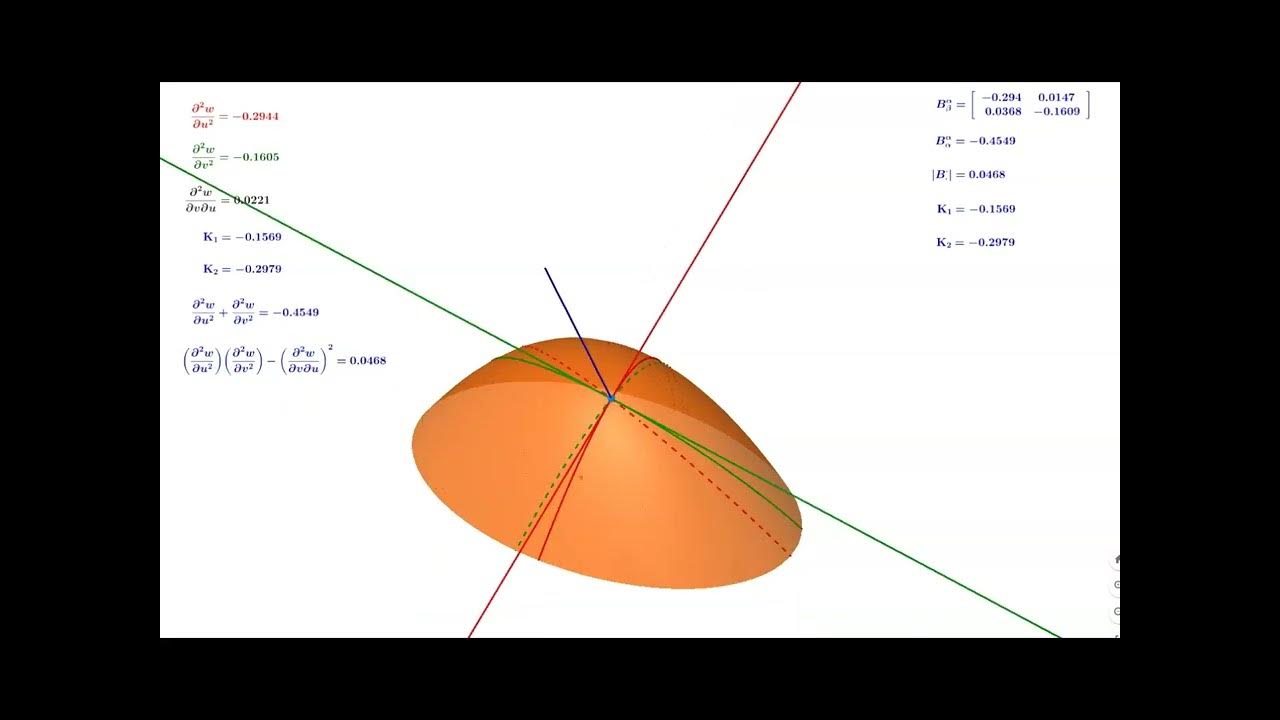
This paragraph introduces the concept of Gaussian curvature, a measure of the curvature of a two-dimensional surface, using an elliptic paraboloid as an example. The video explains how to construct a tangent plane at a given point on the surface and how to define a normal vector. It also discusses the process of finding the curvature of a curve on the surface by taking the second derivative of the function representing the curve with respect to a coordinate axis. The curvature at a point is illustrated by rotating a line in the tangent plane and observing how the curvature changes, leading to the identification of the maximum curvature at a particular direction.
📏 Principal Curvatures and Their Directions
The paragraph delves into the process of finding the principal curvatures of a surface at a given point. It describes the construction of two intersecting lines within the tangent plane, each representing a different direction of curvature. By rotating these lines, the video demonstrates how to locate the directions that yield the maximum and minimum curvature values, known as the principal curvatures. The axes constructed for these principal curvatures are always perpendicular to each other, and the mixed second derivative of the surface function with respect to these axes vanishes, indicating the principal curvatures have been found. The paragraph also discusses the analytical approach to determine the exact angles for these axes without graphical rotation.
🔍 Intrinsic Properties of Surface Curvature
This section discusses the intrinsic properties of a surface's curvature, including the mean curvature and Gaussian curvature. The mean curvature is defined as the average of the two principal curvatures, while the Gaussian curvature is the product of the principal curvatures. The paragraph explains that these quantities are invariant, meaning they do not change with the rotation of the coordinate system. It also highlights two specific invariants: the sum of the second derivatives and a formula involving the product and square of the second derivatives. The video emphasizes that Gaussian curvature is an intrinsic property of the surface, independent of the normal direction, making it a fundamental characteristic of the space itself.
🔄 Curvature Analysis on Different Surfaces
The paragraph explores how the concepts of principal curvatures, mean curvature, and Gaussian curvature apply to different surfaces by changing the shape of the elliptic paraboloid. It demonstrates that a simple paraboloid can have an intrinsic curvature of zero, indicating it can be flattened without distortion, despite appearing curved. The video then examines a hyperbolic paraboloid, where the principal curvatures have opposite signs, resulting in a negative Gaussian curvature. This example illustrates that the Gaussian curvature can be negative when curvatures in different directions oppose each other.
🌐 Tensor Calculus and Curvature Tensor
In the final paragraph, the video script hints at the connection between the concepts discussed and tensor calculus. It promises to bridge the gap between the mathematical analysis of curvature performed in the video and tensor calculus in the next video. The focus will be on the properties of the curvature tensor, which provides a more efficient method for deriving curvature values than the manual process demonstrated in the video. This sets the stage for a deeper exploration of tensor calculus in relation to surface curvature.
Mindmap
Keywords
💡Gaussian Curvature
💡Elliptic Paraboloid
💡Tangent Plane
💡Covariant Basis Vectors
💡Normal Vector
💡Principal Curvatures
💡Mean Curvature
💡Second Derivative
💡Intrinsic Curvature
💡Hyperbolic Paraboloid
Highlights
Introduction of Gaussian curvature as a measure of the curvature of a two-dimensional surface.
Use of an elliptic paraboloid to illustrate the concept of Gaussian curvature.
Construction of a tangent plane at a point on the surface and the identification of basis vectors and normal vector.
Explanation of how to define a plane by intersecting lines within the tangent plane.
Visualization of the intersection as a two-dimensional function in a plane.
Derivation of the curvature of the intersected line using the second derivative.
Demonstration of how the curvature changes with the direction of the intersecting line.
Identification of the maximum and minimum curvatures, known as principal curvatures.
The discovery by Carl Friedrich Gauss that principal curvatures can be found at any point on any surface.
Gauss's observation that the axes of maximum and minimum curvature are perpendicular to each other.
The mixed derivative's role in finding principal curvatures by vanishing at the point of interest.
Introduction of mean curvature as an invariant value, the sum of the principal curvatures.
Definition of Gaussian curvature as an intrinsic property of the surface, the product of the principal curvatures.
Explanation of the independence of Gaussian curvature from the direction of the normal.
Illustration of how surfaces like a paraboloid can have intrinsically flat curvature despite appearing curved.
Demonstration of a hyperbolic paraboloid where curvatures move in opposite directions, resulting in negative Gaussian curvature.
The upcoming integration of tensor calculus to derive curvature properties more efficiently.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: