Limits Calculus Grade 12

Kevinmathscience
18 Sept 202005:08
EducationalLearning
32 Likes 10 Comments

TLDRThis video offers a simplified approach to understanding limits in mathematics, focusing on practical exam strategies rather than complex theories. The presenter suggests initially plugging in the limit value to see if it yields a result without errors. If not, they recommend factorizing or simplifying the expression to avoid division by zero. Examples are provided to illustrate the process, emphasizing the importance of correctly writing 'limit as x approaches a value' and adjusting the expression accordingly. The goal is to simplify to a form that can be evaluated without errors, highlighting a straightforward method suitable for high school students.

Takeaways
  • 📘 Limits are a fundamental concept in calculus, often tested in high school and introduced in more depth at the university level.
  • 🔍 The first step in evaluating a limit is to plug the limit value into the expression to see if it yields a valid result without errors.
  • ❗ If plugging in the limit value results in an error, such as division by zero, further steps are required to resolve the issue.
  • 🔄 When direct substitution is not possible, factorization can be a useful technique to simplify the expression and cancel out terms.
  • 📚 Teachers and exam departments emphasize the importance of using the correct notation, such as 'equals to limit as x goes to...'.
  • 👉 It's crucial to keep writing the limit notation until the actual value is substituted into the expression.
  • 📉 In cases where the denominator becomes zero, limits catch the potential for undefined expressions, which must be addressed.
  • 📌 The script provides examples of how to handle expressions that initially seem to lead to division by zero, by showing how to cancel terms.
  • 🔢 For expressions that simplify to zero over a non-zero denominator, the limit is simply the result of the simplified expression.
  • 🚫 The script warns against the common mistake of having a zero in the denominator, which would cause an error on a calculator.
  • 📝 The final takeaway is a summary of the process: plug in the value, simplify if necessary, and then evaluate the limit.
Q & A

  • What is the main idea behind the concept of limits in mathematics?

    -The main idea behind limits is to understand the behavior of a function as the input approaches a certain value, even if the function is not defined at that point.

  • Why is there an emphasis on plugging in the limit value first when solving limits?

    -Plugging in the limit value first is a simple and quick method to check if the limit exists without encountering any mathematical errors, such as division by zero.

  • What is the first step recommended in the script for solving limit problems?

    -The first step is to try plugging the limit value directly into the expression to see if it yields a valid result without any errors.

  • What happens if plugging in the limit value results in an error on the calculator?

    -If an error occurs, such as division by zero, it indicates that the limit does not exist in the straightforward form, and further steps like factorization or simplification are needed.

  • Why is it important to write 'equals to limit' when approaching a certain value?

    -Writing 'equals to limit' helps to clearly indicate that the variable is approaching a specific value, which is crucial for understanding the process of finding the limit.

  • Can you provide an example of a situation where factorization helps in finding the limit?

    -In the script, the example of the function (x^2 + 3x + 4) / (x + 1) where x approaches -1, factorization allows the cancellation of the (x + 1) term in the numerator and denominator, simplifying the limit to -5.

  • What is the significance of the denominator becoming zero in the context of limits?

    -A denominator becoming zero indicates a point of discontinuity or an undefined point in the function, which is where limits are particularly useful to determine the behavior of the function around that point.

  • How does the script suggest dealing with a zero denominator when finding a limit?

    -The script suggests factorizing the expression to cancel out the terms that lead to a zero denominator, allowing for the limit to be determined without errors.

  • What is the final step in finding the limit after simplification or factorization?

    -The final step is to plug the value of the limit into the simplified expression to find the actual limit value.

  • Can you give an example of a limit problem where plugging in the value directly gives the correct answer?

    -In the script, the example of the function (x - 1) / (x + 1) where x approaches 1, plugging in 1 directly results in 0/2, which simplifies to 0, giving the correct limit.

Outlines
00:00
📚 Understanding Limits in Calculus

This paragraph introduces the concept of limits in calculus, explaining that while there's complex math involved, an easy approach can often be applied, especially for high school exams. The speaker suggests plugging the limit value directly into the expression to see if it yields a valid result on a calculator. If an error occurs, such as division by zero, the student is advised to factorize or simplify the expression before trying again. The paragraph provides a step-by-step example of how to handle a limit problem where the denominator becomes zero by factorizing and canceling terms, ultimately leading to a successful limit calculation.

05:00
🔍 Advanced Limit Calculation Techniques

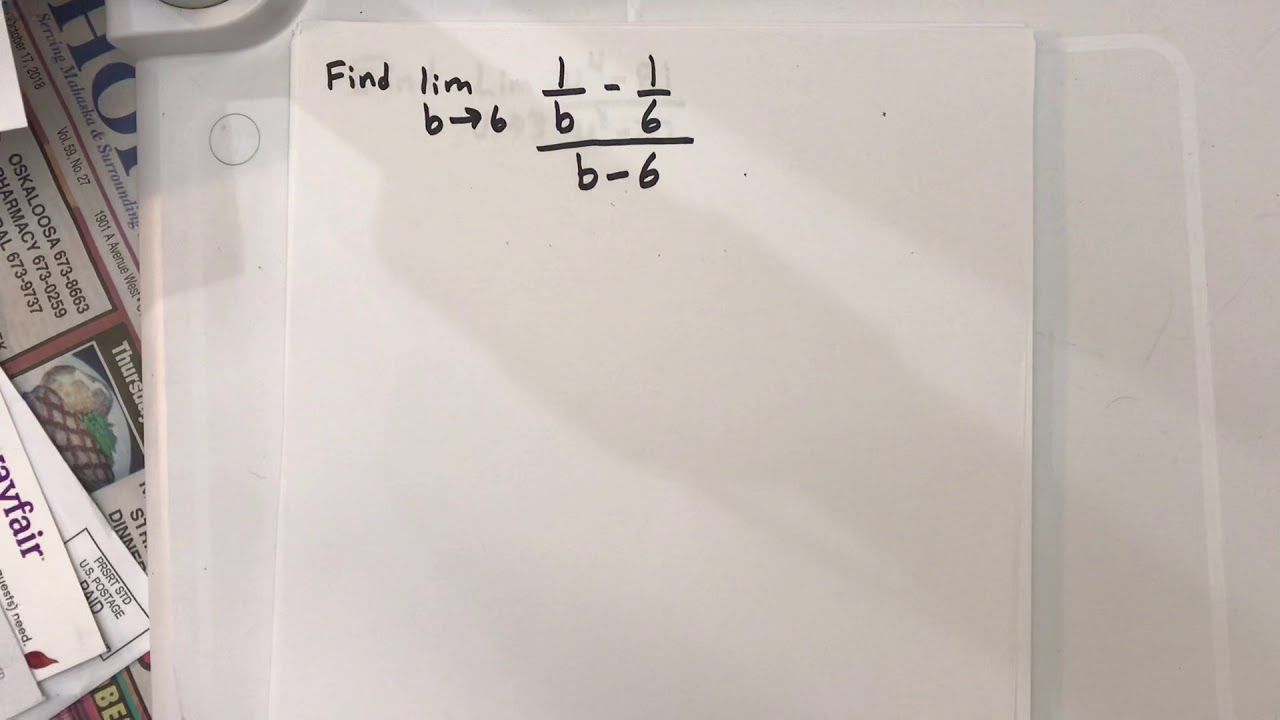
The second paragraph delves into more advanced techniques for calculating limits, emphasizing the importance of correctly writing the limit notation and the process of plugging in the limit value. It discusses a scenario where the direct substitution of the limit value results in an error due to a zero denominator. The paragraph illustrates how to resolve this by identifying and canceling terms, transforming the expression into a form that allows for successful limit evaluation. The example concludes by showing the correct substitution of the limit value, resulting in a final answer of 4, and highlights the significance of maintaining proper mathematical notation throughout the process.

Mindmap
Keywords
💡Limits
Limits are a fundamental concept in calculus that describe the behavior of a function as the input approaches a certain value. In the video, the concept is introduced as a topic that can be approached simply, especially for grade 12 exams, by plugging in the limit value into the function to see if it yields a valid result without errors on a calculator.
💡In-depth Maths
This term refers to the more complex mathematical principles that underlie the concept of limits. While the video suggests that the exams and classroom explanations may not delve into these complexities until university level, it acknowledges their existence and importance in a complete understanding of limits.
💡Plugging in the Value
This is the initial method suggested in the video for finding limits by substituting the limit value directly into the function. It's a straightforward approach that works when the function does not result in any mathematical errors, such as division by zero.
💡Errors on Calculator
The video uses the term to describe situations where plugging in the limit value results in an invalid mathematical operation, such as division by zero. This indicates that the direct substitution method is not applicable, and further steps are needed to find the limit.
💡Denominator
The denominator is the bottom part of a fraction. In the context of limits, if the denominator becomes zero when the limit value is plugged in, it signifies an undefined expression, which is a key area where limits are examined.
💡Factorize
Factorization is the process of breaking down a polynomial into its factors. In the video, it is presented as a method to simplify expressions when direct substitution results in an error, particularly when the denominator can be canceled out with a factor from the numerator.
💡Trinomial
A trinomial is a polynomial with three terms. The video script mentions trinomials in the context of factorization, where a trinomial can be factored into simpler binomials, aiding in the process of finding limits.
💡Cancellation
Cancellation refers to the process of eliminating a common factor from both the numerator and the denominator of a fraction, simplifying the expression. The video explains that exams are designed such that if direct substitution fails, cancellation through factorization can be used to find the limit.
💡Zero at the Bottom
This phrase is used in the video to describe a critical error state where the denominator of a fraction becomes zero, which is not allowed in mathematics. It is a situation that requires the use of factorization or other methods to resolve before finding the limit.
💡Difference of Squares
The difference of squares is a specific factorization pattern where a squared term minus another squared term can be factored into the product of the sum and difference of the two terms. In the video, it's used as an example of how to simplify an expression before finding the limit by direct substitution.
💡Simplify
Simplification in the context of the video refers to the process of making a mathematical expression easier to work with, typically by factorization or cancellation, to facilitate the process of finding limits.
Highlights

Exploring the concept of limits in an easy-to-understand manner for grade 12 students.

Introduction of an easy method to calculate limits by plugging in the limit value into the expression.

Explanation of when to expect errors on the calculator, specifically when the denominator becomes zero.

Guidance on how to handle errors by factorizing the expression when direct plugging in fails.

Emphasis on the importance of writing 'equals to limit' and the process of approaching the limit value.

Demonstration of how to cancel terms in the expression to simplify the limit calculation.

Example of calculating the limit as x approaches -1 by factorizing and canceling terms.

Result of the limit calculation as x approaches -1, yielding the answer -5.

Approach to handle limits involving zero in the denominator by factorizing and simplifying.

Calculation of the limit as x approaches zero, resulting in the answer 3.

Explanation of how to deal with a zero numerator and non-zero denominator when calculating limits.

Illustration of a limit calculation where the numerator becomes zero, resulting in a limit of 0.

Handling a limit problem where the denominator becomes zero by factorizing and canceling.

Final result of the limit as x approaches 2, which is 4, after factorizing and simplifying.

Summary of the limit calculation process: plug in the value, factorize if needed, and check for calculator errors.

Reiteration of the importance of the 'equals to limit' notation and the step-by-step approach to limits.

Highlighting the practicality of the method for grade 12 exams and its alignment with educational standards.

Transcripts

Browse More Related Video

1.2 - Algebraic Limits and Continuity

Example (2.2) - Finding the limit of a function #13 (Calc)

Business Calculus - Math 1329 - Section 1.5 (and 1.6) - Limits and Continuity

Example (2.2) - Finding the limit of a function #14 (Calc)

Applying the Definition of the Derivative to 1/x

Business Calculus - Math 1329 - Section 1.5 (Part 1) - Limits and Continuity

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsLimitsCalculusHigh SchoolExam TipsSimplified MathFactorizationCalculator ErrorsEducational ContentMath TutorialLimit Examples