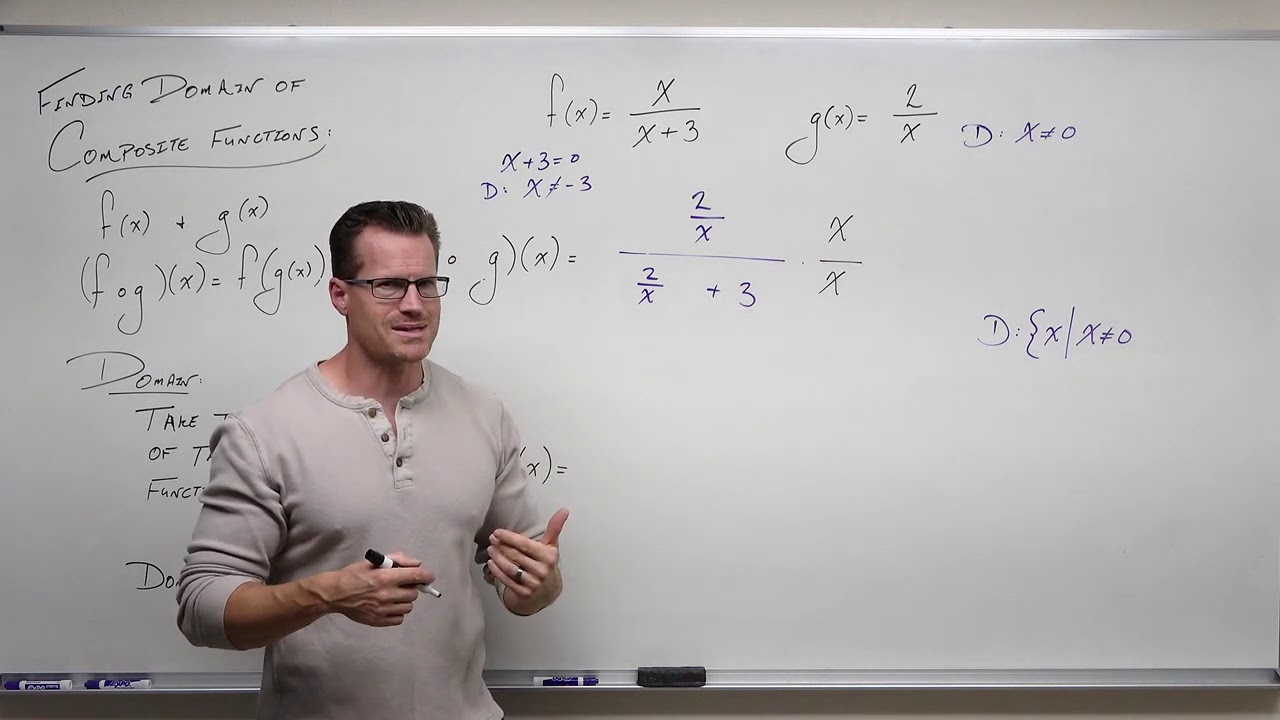How to Find the Domain of a Composite Function
TLDRThis educational video delves into the intricacies of finding the domain of composite functions, a common stumbling block for students. The instructor methodically explains the process, starting with identifying the domain restrictions of the inner function and then finding the composite function itself. Through several examples, the video illustrates how to handle different scenarios, including polynomials, square roots, and functions with denominators, emphasizing the importance of excluding values that would make the inner function undefined. The clear explanations and step-by-step approach aim to demystify the concept and equip viewers with the skills to tackle such problems with confidence.
Takeaways
- 🧠 Understanding the domain of composite functions is crucial, especially when working with functions like F(x) and G(x).
- 🔍 The first step is to identify domain restrictions of the inner function (G(x)).
- ✅ If the inner function has no domain restrictions, the domain of the composite function could be all real numbers.
- 🔗 When finding a composite function, you substitute G(x) into F(x) and then simplify.
- 📏 After simplification, check the domain of the composite function to see if any additional restrictions apply.
- 🚫 If the inner function has restrictions (like division by zero or negative square roots), those restrictions must also apply to the composite function.
- 🔄 In interval notation, express the domain by excluding restricted values, such as points where the function is undefined.
- 📝 Example: If G(x) has a square root, ensure the expression inside the square root is non-negative.
- ⚠️ Common mistake: Forgetting to apply restrictions from the inner function when determining the domain of the composite function.
- 🎯 The final domain of a composite function is the intersection of the domains of the inner and composite functions.
Q & A
What is the main topic of the video?
-The main topic of the video is about finding the domain of a composite function in mathematics.
What is a composite function?
-A composite function is a function that is formed by applying one function to the result of another function. It is typically represented as F(G(x)) where F is the outer function and G is the inner function.
Why is finding the domain of a composite function tricky?
-Finding the domain of a composite function is tricky because it requires identifying the domain restrictions of the inner function first and then ensuring that the output of the inner function is within the domain of the outer function.
What is the first step in finding the domain of a composite function?
-The first step is to identify the domain restrictions of the inner function.
What does the video suggest for the domain of a composite function made from two functions with all real numbers as their domain?
-The video suggests that if both functions have a domain of all real numbers, then the composite function will also have a domain of all real numbers.
What is an example of a restriction in the domain of a function?
-An example of a restriction in the domain of a function is when there are values that cannot be plugged into the function, such as negatives under a square root or zeros in the denominator.
How does the video demonstrate the process of finding the composite function?
-The video demonstrates the process by plugging the inner function (G(x)) into the outer function (F) and simplifying the result.
What is the importance of considering the domain restrictions of the inner function first?
-The importance is that every number has to go through the inner function first, so if there are values excluded from the domain of the inner function, they must also be excluded from the composite function.
How does the video handle the example where the inner function has a square root?
-The video sets the expression under the square root to be greater than or equal to zero to find the domain restrictions, and then plugs the inner function into the outer function while keeping these restrictions in mind.
What is the common mistake made when finding the domain of a composite function involving linear functions?
-The common mistake is to assume that the domain is all real numbers without considering the domain restrictions of the inner function that must be applied to the composite function.
How does the video explain the domain of a composite function involving fractions?
-The video explains that if there are fractions in the composite function, you must ensure the denominator is not zero, and these values are excluded from the domain of the composite function.
Outlines
🔍 Understanding Composite Functions and Their Domains
This paragraph introduces the topic of composite functions and the challenge of determining their domains. The speaker explains that composite functions consist of an inner and an outer function, and the domain of the inner function is crucial. An example is given where the inner function has no domain restrictions, leading to a composite function with a domain of all real numbers. The paragraph emphasizes the importance of identifying domain restrictions and demonstrates the process with a simple example involving squaring the inner function's output.
📚 Domain Restrictions in Composite Functions
The second paragraph delves deeper into the concept of domain restrictions, particularly focusing on how they affect composite functions. The speaker illustrates this with an example where the inner function has a domain restriction of excluding zero, due to division by zero. The composite function is then found by substituting the inner function into the outer function, resulting in a new function with its domain restricted by both the inner function's exclusion of zero and the outer function's requirement for a non-zero denominator. The domain is expressed in interval notation, highlighting the excluded values.
📉 Addressing Domain Limitations with Square Roots and Linear Functions
In this paragraph, the discussion continues with an example involving a square root in the inner function, which imposes a restriction that the input must be greater than or equal to 1. The speaker then finds the composite function by substituting the inner function into the outer function, resulting in a linear function. It is emphasized that despite the simplicity of the resulting function, the domain is restricted by the inner function's domain, meaning the composite function's domain only includes values greater than or equal to 1. The importance of not overlooking the domain restrictions of the inner function is highlighted.
📘 Simplifying Composite Functions with Fractions and Identifying Domain Exclusions
The final paragraph presents a complex example involving fractions and demonstrates the process of simplifying the composite function. The inner function has a domain restriction where the denominator cannot be zero, excluding the value 2. The composite function is found by substituting the inner function into the outer function, leading to a simplified expression. The domain of the composite function is then determined by considering both the inner function's restriction and the resulting function's requirement for a non-zero denominator, which excludes the value 3/2. The final domain is presented, and the paragraph concludes with an invitation for viewers to practice similar problems.
Mindmap
Keywords
💡Composite Functions
💡Domain
💡Inner Function
💡Outer Function
💡Domain Restrictions
💡Polynomials
💡Quadratic Functions
💡Linear Functions
💡Interval Notation
💡Square Root
💡Denominator
Highlights
Introduction to composite functions and focus on finding the domain.
Step-by-step approach to finding the domain of a composite function by first identifying domain restrictions of the inner function.
Example 1: Both functions have domains of all real numbers, making the domain of the composite function also all real numbers.
Important note: When dealing with polynomials, quadratics, and linear functions, the domain of the composite function is usually all real numbers.
Example 2: Handling a function with a denominator, emphasizing the need to exclude values that cause the denominator to be zero.
Explanation of why domain restrictions from the inner function must be carried over to the composite function.
Detailed algebraic steps to simplify the composite function and identify additional domain restrictions.
Use of interval notation to express the domain, and how to handle multiple restrictions.
Example 3: Working with a square root function, explaining the importance of ensuring the argument under the square root is non-negative.
Common mistake highlighted: Ignoring initial domain restrictions from the inner function.
Final example with a function that has both a square root and a denominator, demonstrating how to combine restrictions from both components.
Step-by-step simplification of the composite function involving multiple algebraic operations.
Identification of final domain restrictions for the composite function, including specific values to exclude.
Use of both set notation and interval notation to express the domain of the composite function.
Conclusion: Summary of key points and encouragement to practice identifying domain restrictions in composite functions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: