How To Find The Domain of a Composite Function | Precalculus

The Organic Chemistry Tutor
28 Sept 202211:42
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script explains how to determine the domain of a composite function by considering the restrictions of individual functions. It illustrates the process using two examples: one with rational functions and another with a polynomial and a square root function. The script emphasizes the importance of understanding that the domain of the composite function is influenced by the domains of its components, and provides a step-by-step guide on how to express the domain in interval notation, ensuring a clear understanding of the concept.

Takeaways
  • 🔍 Understanding the domain of composite functions is crucial when solving mathematical problems.
  • ⚠️ For the function G(x) = 1/x, the value of x cannot be zero because it would make the denominator undefined.
  • 🚫 In the function f(x) = 4/(x + 2), x cannot be equal to -2 as it would result in division by zero.
  • 🤔 When determining the domain of a composite function f(g(x)), the restrictions of both f(x) and g(x) must be considered.
  • 🧮 Substituting g(x) into f(x) can create new restrictions, such as ensuring that g(x) remains within the domain of f(x).
  • 🔄 In the example, x = -1/2 is identified as a value that will not work in the composite function f(g(x)) because it would lead to an undefined value.
  • ➗ Simplifying the composite function by eliminating complex fractions can help reveal additional domain restrictions.
  • 📉 Graphically, the domain of a composite function can be represented on a number line, indicating the values x cannot take.
  • 🟢 For the polynomial function f(x) = x² + 3, there are no restrictions on x, but the square root function in g(x) = √(4-x) imposes a restriction.
  • 📏 The final domain of the composite function f(g(x)) is determined by combining the restrictions of both functions, ensuring all conditions are met.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is how to find the domain of a composite function.

  • What are the given functions f(x) and g(x) in the video?

    -The given functions are f(x) = 4 / (x + 2) and g(x) = 1 / x.

  • Why can't x be zero in the function g(x)?

    -X cannot be zero in g(x) because it would result in a division by zero, which is undefined.

  • What is the limitation for x in the function f(x)?

    -The limitation for x in f(x) is that x + 2 cannot be zero, which means x cannot be negative two.

  • How does the domain of the composite function f(g(x)) differ from the individual domains of f(x) and g(x)?

    -The domain of the composite function f(g(x)) takes into account the restrictions from both f(x) and g(x), and also considers the interaction between the two functions.

  • Can x be negative two in the composite function f(g(x))?

    -Yes, x can be negative two in the composite function f(g(x)) because it does not result in an undefined value within the composite function.

  • What x value would make g(x) equal to negative two, and why is this problematic for the composite function?

    -The x value that would make g(x) equal to negative two is x = -1/2. This is problematic because when plugged into f(x), it results in a zero in the denominator, making the function undefined.

  • How can the domain of the composite function be expressed on a number line?

    -The domain of the composite function can be expressed on a number line with an open circle at x = -1/2 and x = 0, shading everything except these two points, from negative infinity to positive infinity.

  • What is the domain of the composite function f(g(x)) in interval notation?

    -The domain of the composite function f(g(x)) in interval notation is (-∞, -1/2) ∪ (-1/2, 0) ∪ (0, ∞).

  • How does the process of finding the domain of a composite function differ from finding the domain of a single function?

    -Finding the domain of a composite function involves considering the domains of both the inner and outer functions and ensuring that the output of the inner function is within the domain of the outer function.

  • Can you provide an example of another composite function and its domain?

    -An example given in the video is f(x) = 5 / (x - 3) and g(x) = 2 / x. The domain of the composite function f(g(x)) would be from negative infinity to 0, then from 0 to 2/3, and from 2/3 to positive infinity, in interval notation: (-∞, 0) ∪ (0, 2/3) ∪ (2/3, ∞).

  • What is the restriction for the function g(x) when it involves a square root, as in the example g(x) = sqrt(4 - x)?

    -The restriction for g(x) when it involves a square root is that the expression under the square root, 4 - x, must be greater than or equal to zero, which means x must be less than or equal to four.

  • How does the domain of a polynomial function like f(x) = x^2 + 3 affect the composite function f(g(x))?

    -Since a polynomial function like f(x) = x^2 + 3 has no restrictions, the domain of the composite function f(g(x)) is determined solely by the restrictions of the inner function g(x), in this case, x ≤ 4.

  • What is the final domain of the composite function f(g(x)) when f(x) is a polynomial and g(x) involves a square root?

    -The final domain of the composite function f(g(x)) when f(x) is a polynomial and g(x) involves a square root is all real numbers from negative infinity to 4, inclusive of 4, represented in interval notation as [-∞, 4].

Outlines
00:00
📚 Understanding Composite Function Domains

This paragraph introduces the concept of finding the domain of a composite function. It uses the example of two rational functions, f(x) and g(x), to demonstrate how to determine the domain of f(g(x)). The explanation covers the individual restrictions of each function and then combines them to find the domain of the composite function. It clarifies that x cannot be zero for g(x) and x cannot be -2 for f(x) when considered individually. However, for the composite function, x can be -2, but not -1/2, as this would result in an undefined value in the denominator. The paragraph concludes with a simplified form of the composite function and emphasizes the importance of considering the domain of the inner function when determining the domain of the composite function.

05:02
📐 Expressing Domain Restrictions on a Number Line

The second paragraph continues the discussion on composite functions by providing a method to express the domain graphically on a number line. It uses the previous example to illustrate how to represent the domain with open circles at points where the function is undefined (x = 0 and x = -1/2). The paragraph explains how to shade the intervals where the function is defined, leading to the interval notation for the domain. It then presents an additional example with different functions, f(x) = 5/(x-3) and g(x) = 2/x, and guides through the process of finding the domain of f(g(x)). The summary includes the steps to simplify the composite function and identify the values that x cannot take, resulting in the domain expressed in interval notation.

10:04
🔍 Further Exploration of Composite Function Domains

The final paragraph delves deeper into the domain of composite functions by introducing a polynomial function f(x) and a square root function g(x). It explains the restriction for g(x) due to the square root, which requires the argument to be non-negative, leading to the domain of g(x) being x ≤ 4. Since f(x) is a polynomial with no restrictions, the composite function f(g(x)) inherits the restriction from g(x). The paragraph simplifies the composite function to 7 - x and confirms that the domain is all real numbers less than or equal to 4. It concludes by describing how to graph this domain on a number line, including a closed circle at the endpoint x = 4, and the interval notation for the domain.

Mindmap
Keywords
💡Domain
The term 'domain' in mathematics refers to the set of all possible input values for a function. In the context of the video, finding the domain of a composite function involves determining the values of 'x' for which the function is defined. The script discusses how to find the domain for individual functions and then combines these to find the domain of the composite function, such as 'f(g(x))', by considering the restrictions imposed by each function.
💡Composite Function
A composite function is a function composed of two or more functions, where the output of one function becomes the input of the next. In the video, the concept is central to understanding how the domain of each individual function affects the domain of the overall composite function. For example, 'f(g(x))' is a composite function where 'g(x)' is substituted into 'f(x)'.
💡Rational Function
A rational function is a fraction where both the numerator and the denominator are polynomials. The script uses rational functions 'f(x) = 4 / (x + 2)' and 'G(x) = 1 / x' to demonstrate the process of finding the domain of a composite function. The domain of a rational function is all real numbers except those which make the denominator zero.
💡Denominator
The 'denominator' of a fraction is the number, expression, or polynomial below the division line. In the context of the video, the denominator is critical because it cannot be zero, as division by zero is undefined. This concept is used to determine the restrictions on the domain of the functions 'f(x)' and 'G(x)'.
💡Undefined Value
An 'undefined value' occurs when a mathematical operation does not have a meaningful result. In the video, the term is used to describe the situation where the denominator of a fraction is zero, such as '1/0', which is not allowed and thus restricts the domain of the function.
💡Interval Notation
Interval notation is a way to express a set of numbers by indicating the lower and upper bounds within which the values of x can lie. The video uses interval notation to express the domain of composite functions, such as '(-∞, -1/2) U (-1/2, 0) U (0, ∞)', which represents all real numbers except -1/2 and 0.
💡Square Root
A square root is a value that, when multiplied by itself, gives the original number. The video mentions square roots in the context of the function 'G(x) = √(4 - x)', where the domain is restricted to values of x that make the expression under the square root non-negative.
💡Polynomial Function
A polynomial function is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. In the video, 'f(x) = x^2 + 3' is an example of a polynomial function, which has a domain of all real numbers since it does not have any restrictions like denominators or square roots.
💡Inequality
An inequality is a mathematical relation that holds between two expressions if one is greater than, less than, or equal to the other. The video discusses how to handle inequalities when determining the domain of functions involving square roots, such as changing the direction of the inequality when multiplying or dividing by a negative number.
💡Restriction
A 'restriction' in the context of functions refers to the limitations on the input values that the function can accept. The video explains how to identify restrictions for individual functions and how these restrictions affect the domain of the composite function, such as excluding values that would result in an undefined expression.
Highlights

Introduction to finding the domain of a composite function.

Given function f(x) = 4 / (x + 2) and g(x) = 1 / x.

Domain restrictions for g(x): x cannot be zero.

Domain restrictions for f(x): x + 2 cannot be zero, so x cannot be negative two.

Composite function f(g(x)) is calculated by substituting g(x) into f(x).

Composite function f(g(x)) = 4 / (1 / x + 2).

X cannot be zero in the composite function due to the denominator.

X can be negative two in the composite function, unlike in f(x) alone.

X cannot be negative one-half because it would make g(x) equal to negative two, invalidating f(x).

Simplifying the composite function by multiplying numerator and denominator by x.

Domain of composite function f(g(x)) is expressed in interval notation.

Second example with f(x) = 5 / (x - 3) and g(x) = 2 / x.

Domain of g(x) restricts x to not equal zero.

Composite function f(g(x)) = 5 / (2 / x - 3) and its domain restrictions.

X cannot be 2/3 in the composite function due to the denominator.

Domain of the second composite function expressed in interval notation.

Third example with f(x) = x^2 + 3 and g(x) = sqrt(4 - x).

Domain of g(x) is restricted by the square root to x ≤ 4.

Composite function f(g(x)) simplifies to 7 - x, with domain restrictions from g(x).

Domain of the third composite function f(g(x)) is all real numbers less than or equal to four.

Transcripts

Browse More Related Video

Composition of Functions (Precalculus - College Algebra 48)

How to Find the Domain of a Composite Function

How To Find The Domain of a Function - Radicals, Fractions & Square Roots - Interval Notation

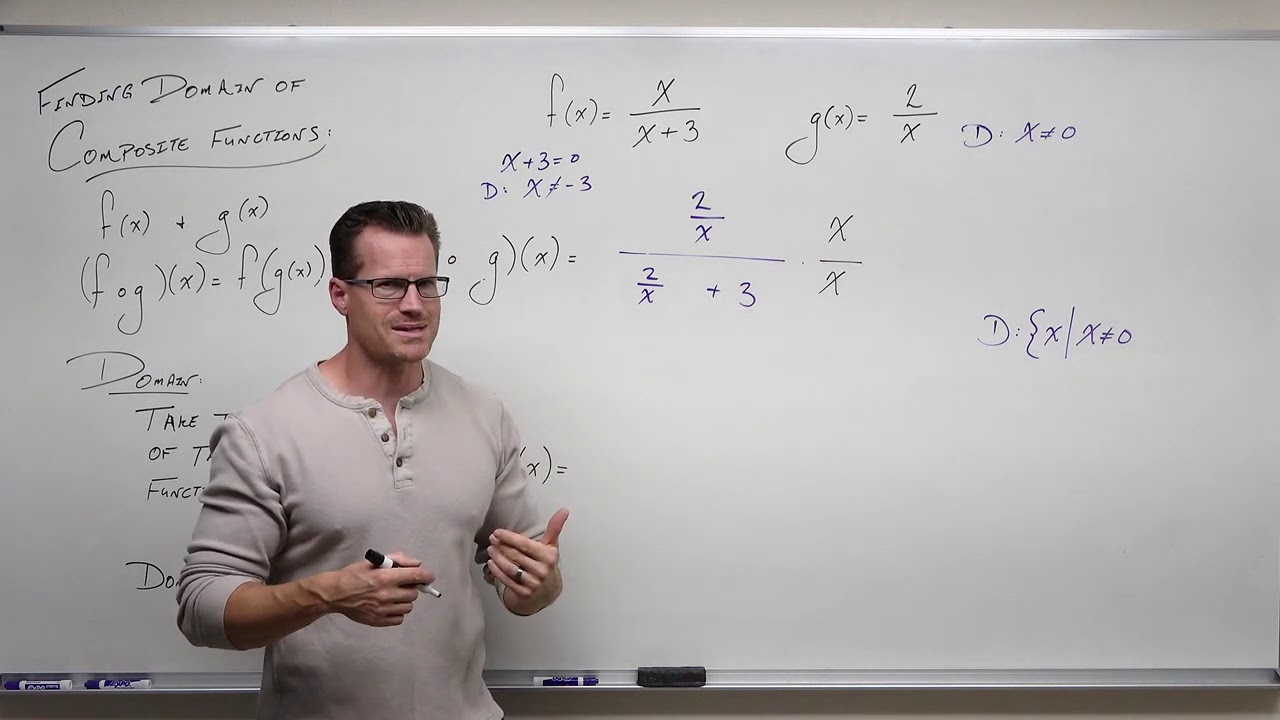
Finding Domain of Composite Functions (Precalculus - College Algebra 49)

How to Find Inverse Trigonometric Functions (Precalculus - Trigonometry 19)

Functions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Composite FunctionsDomain AnalysisMathematics TutorialRational FunctionsFunction RestrictionsAlgebraic ConceptsEducational ContentMath PracticeFractional DomainsRoot Functions