Lecture 10: Clicker Bonanza and Dirac Notation
TLDRIn this educational transcript, a professor excitedly announces an upcoming addition to their family and proceeds to discuss an upcoming exam format change. The lecture covers various quantum mechanics concepts, including eigenfunctions, the superposition principle, and the Dirac Bra-Ket notation. The professor uses clicker questions to engage students in understanding wave functions, energy eigenstates, and the implications of non-commuting operators, such as position and momentum, which leads into Heisenberg's uncertainty principle. The session is interactive, with students participating in discussions and clarifying doubts.
Takeaways
- 🎓 The professor announces a change in the exam format to reduce burden and provide more useful feedback, emphasizing the exam's purpose is to assess conceptual understanding.
- 📅 The exam location has been rescheduled to 6120, not in Walker Gym, and the exam will cover material through the last problem set, excluding the current day's lecture.
- 📝 The exam will start with short answer questions, including computations, followed by a review and introduction to the Dirac Bra-Ket notation.
- 🤔 The professor discusses the absence of a practice exam due to format changes, suggesting that the day's activities will serve as practice.
- 🔢 During the lecture, clicker questions are used to gauge student understanding and prepare them for the exam, with the promise to post these questions on the website.
- 📊 A discussion on eigenfunctions and eigenvalues takes place, highlighting the importance of understanding the superposition principle and energy eigenstates.
- 👶 The professor shares personal news of expecting a baby, lightening the mood and making the class more relatable.
- 📚 The lecture includes an interactive component with clicker questions to engage students and provide immediate feedback on their understanding.
- 🤷♂️ The professor addresses the challenge of certain conceptual questions, even without computation, emphasizing the importance of grasping quantum mechanics' fundamental principles.
- 📈 The lecture explores the implications of the uncertainty principle, the role of commutators in quantum mechanics, and their relation to observables.
- 🤔 The professor encourages students to ask questions, reflecting an open and inclusive teaching style that values student curiosity and engagement.
Q & A
What is the purpose of the exam according to the professor's explanation?
-The purpose of the exam is not only to assign grades but also to provide students with feedback on their progress and to help them learn concepts they might not have mastered yet.
What is the format of the upcoming exam?
-The exam will consist of approximately 15 minutes of short answer questions, including a few computations, and will be relatively low pressure and mostly conceptual.
Why did the professor decide to change the exam format?
-The professor changed the exam format to make it less burdensome for the students and to make the exam more useful by focusing on the students' conceptual understanding.
What will be the structure of the exam in comparison to the clicker questions used in class?
-The exam will be slightly harder than the clicker questions, but the main difference is that it will be on paper, allowing students more room to perform short calculations.
Will there be a practice exam available for students?
-The professor is unsure if there will be a practice exam due to the shift in format, but if one is available in the correct format, it might be provided.
How will the professor address the issue of the clicker questions not working properly during class?
-The professor will try to troubleshoot the issue and ensure that the clicker questions are saved in memory, and will attempt to retrieve the responses when the app malfunctions.
What is the significance of the Dirac Bra-Ket notation in the lecture?
-The Dirac Bra-Ket notation is used in many textbooks but has not been introduced in lectures so far. It is an essential tool for representing quantum states and operators.
Why did the professor emphasize that the energy operator is just energy and nothing else?
-The professor emphasized this to clarify that the energy operator represents the energy of the system in quantum mechanics and should not be confused with other concepts.
What is the implication of the Hamiltonian operator being Hermitian?
-The Hamiltonian operator being Hermitian implies that it has real eigenvalues and a complete set of eigenfunctions, which are orthogonal and can be used as a basis for the state space.
How does the professor explain the concept of energy eigenfunctions being real or imaginary?
-The professor mentions that for potentials with only bound states, the energy eigenfunctions can always be expressed as purely real or purely imaginary, which will be proven in a problem set.
What is the significance of the commutator in quantum mechanics?
-The commutator is significant because it tells us about the possibility of having common eigenstates for two operators. If the commutator of two operators is non-zero, they cannot have common eigenstates, which is related to the uncertainty principle.
Outlines
📚 Introduction to MIT OpenCourseWare and Class Announcements
The script begins with an introduction to MIT OpenCourseWare, emphasizing its mission to provide free educational resources under a Creative Commons license. The professor then announces a change in the exam schedule, moving it from Walker Gym to room 6120, and explains the new exam format, which will be less burdensome and more focused on providing feedback. The exam will consist of short answer questions, with a review of the last problem set and a preview of the Dirac Bra-Ket notation to follow in the lecture. The professor also shares personal news of expecting a baby, eliciting applause from the class.
🔍 Review of Exam Format and Clicker Questions
The professor reviews the format of an upcoming exam, which will include short answer questions and emphasizes its conceptual nature. The exam will cover all material through the last problem set, with the current lecture's content reserved for the next midterm in April. The lecture proceeds with clicker questions to familiarize students with the exam's level and scope. The professor also addresses technical difficulties with the clicker system during the session.
🌐 Discussion on Eigenfunctions and Schrodinger Equation
The lecture continues with a discussion on eigenfunctions and the Schrodinger equation, focusing on the properties of solutions to these equations. Students are engaged in a clicker question about the sum of two solutions of the Schrodinger equation, highlighting the superposition principle. The professor also explains the concept of an infinite square well and its ground state energy, using intuitive and physical reasoning to clarify the concepts.
📈 Time Evolution of Wave Functions and Eigenvalue Problems
The professor delves into the time evolution of wave functions in an infinite square well, discussing the relationship between the time-zero wave function and its subsequent states. The explanation includes the use of energy eigenfunctions and the superposition principle to determine the time evolution. The lecture also covers the process of finding expansion coefficients for wave functions and emphasizes the importance of understanding the underlying physics.
🚀 Orthonormal Sets and Expectation Values in Quantum States
The script explores the concept of orthonormal sets in quantum mechanics, leading to a discussion on the expectation values of quantum states. The professor uses the example of the Hamiltonian operator and its action on eigenstates to illustrate how expectation values are calculated. The lecture also clarifies the difference between the energy operator and the Hamiltonian, emphasizing the importance of understanding the physical meaning behind mathematical terms.
📉 Analysis of Wave Function Curvature and Probabilities
The lecture examines the curvature of wave functions in classically allowed and disallowed regions, using graphical representations to aid understanding. The professor explains how the curvature is indicative of the wave function's behavior and its relation to the potential energy. The session also touches on the probabilistic nature of quantum mechanics and how wave functions provide information about the likelihood of measuring certain properties.
🔄 Time Evolution and Expectation Values in Quantum Systems
The professor discusses the time evolution of quantum systems, particularly the expectation values of energy and position. The lecture clarifies that while the expectation value of energy remains constant in time for time-independent potentials, the expectation value of position can change. The session also addresses the concept of energy conservation in quantum mechanics and its relation to the expectation value of energy.
🎯 Measurement Outcomes and Probabilities in Quantum States
The script focuses on the outcomes of measurements in quantum states and the associated probabilities. The professor explains the consequences of measuring observables A and B, and how the state of the system changes immediately after each measurement. The lecture also explores the probabilities of obtaining specific eigenvalues upon subsequent measurements, emphasizing the role of the wave function and its coefficients in determining these probabilities.
🚫 Physical and Mathematical Limitations of Potential Functions
The lecture addresses the limitations of potential functions in quantum mechanics, discussing the physical and mathematical constraints that govern their behavior. The professor explains why certain potential functions, such as those that are unbounded from below, are not physically viable. The session also touches on the concept of Hermitian operators and their importance in quantum mechanics, as well as the challenges of constructing physical potentials with certain characteristics.
🔑 The Role of Raising and Lowering Operators in Quantum Mechanics
The professor discusses the role of raising and lowering operators in quantum mechanics, particularly in relation to the energy eigenstates of a system. The lecture explains that these operators do not always commute with the energy operator in a way that maintains evenly spaced energy levels. The session also explores the conditions under which raising and lowering operators can be defined and their significance in the context of the harmonic oscillator.
💡 The Significance of the Ground State in Quantum Systems
The lecture delves into the significance of the ground state in quantum systems, explaining the conditions that lead to the existence of a lowest energy state. The professor discusses the mathematical and physical reasoning behind the requirement for a ground state to be annihilated by the lowering operator, and how this ensures that the energy of the system is bounded from below.
📝 Concluding Remarks and Upcoming Lecture Topics
In the final paragraph, the professor wraps up the lecture with a brief overview of the topics covered and hints at the upcoming lecture content. The session concludes with a reminder for students to review the posted notes and a preview of the introduction to Dirac notation and the significance of commutators in quantum mechanics.
🔬 Deep Dive into Commutators and Uncertainty Principles
The professor introduces the concept of commutators in quantum mechanics, explaining their role in determining whether two observables can have definite values simultaneously. The lecture explores the relationship between commutators and the uncertainty principle, using the example of position and momentum operators to illustrate the fundamental limits on the precision with which these quantities can be known concurrently.
Mindmap
Keywords
💡Creative Commons license
💡MIT OpenCourseWare
💡Exam format
💡Short answer questions
💡Clicker questions
💡Dirac Bra-Ket notation
💡Eigenfunctions and eigenvalues
💡Schrodinger equation
💡Infinite square well
💡Wave function
💡Superposition principle
💡Hamiltonian
💡Orthonormal set
💡Expectation value
💡Uncertainty principle
Highlights
Professor announces the rescheduling of the exam to room 6120 and the change in exam format.
Introduction of the new exam format to reduce burden and provide more useful feedback to students.
Explanation of the exam's purpose beyond grading, focusing on feedback and material mastery.
Structure of the exam includes 15 minutes of short answer and computation questions.
Announcement that the exam will not cover the day's lecture but will be part of the next midterm.
Use of clicker questions during the lecture to gauge exam readiness and provide a review.
Clarification that there will likely be no practice exam due to the format change.
Discussion on the posting of clicker questions from the current and last class on the website.
Exploration of eigenfunctions and eigenvalues through clicker questions in a classroom互动.
In-depth analysis of the Schrodinger equation and its solutions using clicker questions.
Explanation of the Dirac Bra-Ket notation and its importance in quantum mechanics.
Discussion on the time evolution of wave functions and their relation to energy eigenfunctions.
Clarification on the process of obtaining coefficients in a wave function superposition.
Introduction to the concept of orthonormal sets and their significance in quantum mechanics.
Analysis of the expectation value of energy in the context of the simple harmonic oscillator.
Discussion on the implications of the Hamiltonian operator in quantum mechanics.
Exploration of the curvature of wave functions in classically allowed and disallowed regions.
Interactive review of quantum mechanics principles through clicker questions and student discussions.
Transcripts
Browse More Related Video

Lecture 5: Operators and the Schrödinger Equation

Lecture 15: Eigenstates of the Angular Momentum Part 1

Ch 10: What's the commutator and the uncertainty principle? | Maths of Quantum Mechanics
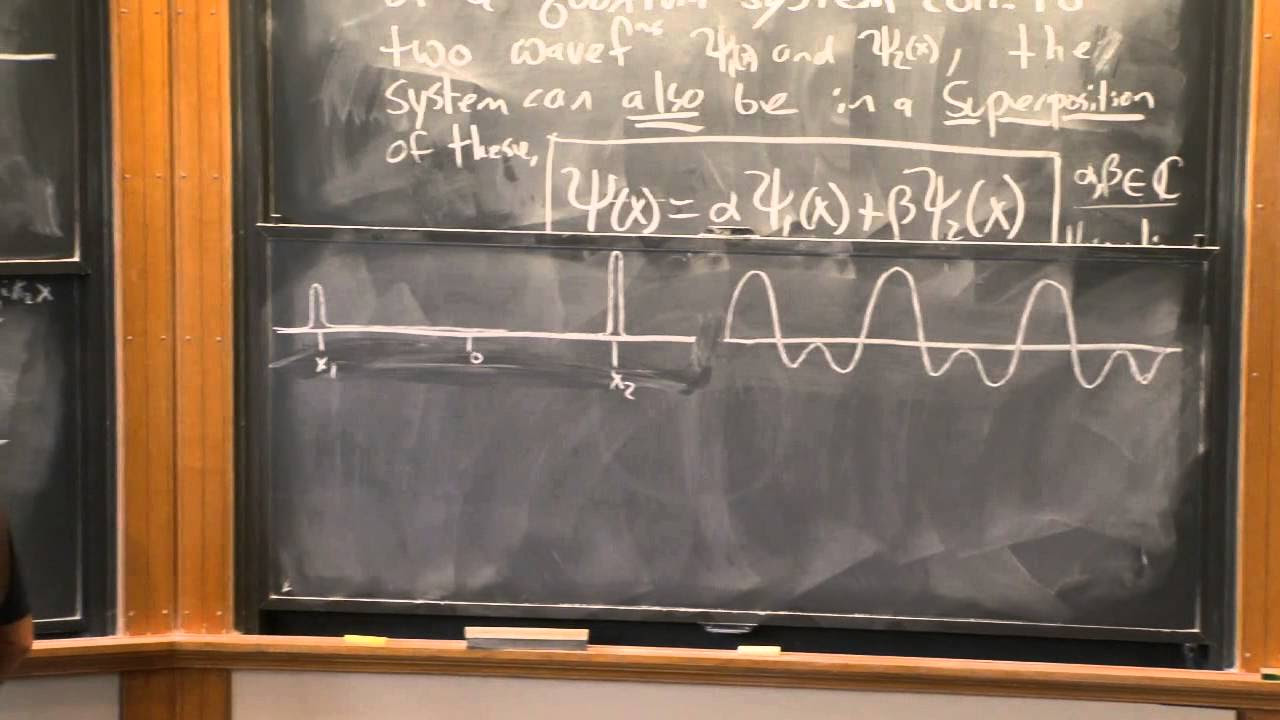
Lecture 3: The Wave Function

Lecture 6: Time Evolution and the Schrödinger Equation

Advanced Quantum Mechanics Lecture 3
5.0 / 5 (0 votes)
Thanks for rating: