Change of Variable, IBP and Improper Integral
TLDRIn this educational video, the host tackles an integration problem involving a quotient of exponential and polynomial functions. They introduce the concept of U-substitution to simplify the integral and guide viewers through the process, including changing the bounds for an improper integral. The host also creatively addresses the challenge of integrating with an infinite upper bound by using limits. The video concludes with the result of the integral, which diverges to positive infinity, and the host encourages viewers to engage with the content to help reach a subscriber milestone.
Takeaways
- 📚 The video is an educational tutorial focused on solving an integration problem involving a quotient function with 'e to the power of 1/x' and 'x cubed'.
- 🔍 The instructor suggests using U-substitution or trigonometric substitution as the quotient rule and product rule for integration do not apply directly to this problem.
- 👉 The choice of U is '1/x' to simplify the integral, and the derivative of U, 'du', is calculated as 'x to the power of -2' or '-x^-2'.
- 🔄 The script involves manipulating the integral to express 'dx' in terms of 'du', aiming to replace 'dx' with a scalar multiple of 'du'.
- ✍️ The integral is rewritten to facilitate the U-substitution, resulting in an expression involving 'u', 'e^u', and 'x squared'.
- 📉 The boundaries of the integral are adjusted from '0 to 1' to 'infinity to 1' after the substitution, reflecting the new limits in terms of 'u'.
- 🚫 The instructor notes that one of the new boundaries is infinity, which indicates an improper integral that requires special handling.
- 🔧 The improper integral is addressed by rewriting it as a limit as 'R' approaches infinity, transforming the integral into a more manageable form.
- 📈 The DI method, a shorthand for integration by parts, is applied to solve the integral, with 'u' chosen for differentiation due to its simplicity.
- 🔚 The final result of the integral is expressed as a limit that approaches infinity, indicating that the integral diverges or is positive infinity.
- 📢 The video concludes with a call to action for viewers to subscribe, like, and share the video to help the channel reach 10,000 subscribers.
Q & A
What is the main topic of the video?
-The main topic of the video is solving an integration problem involving a quotient function with e to the power of 1/x and x cubed in the denominator.
What are the integration techniques mentioned in the video?
-The video mentions U-substitution, trigonometric substitution, and integration by parts as potential techniques for solving the given integration problem.
Why does the video creator choose U-substitution for this problem?
-The video creator chooses U-substitution because the function e to the power of 1/x can be set as 'U', making it easier to handle and integrate the rest of the function.
What is the derivative of U when U is set to 1/x?
-The derivative of U, when U is set to 1/x, is -x to the power of -2, which can be written as -1/x^2.
How does the video creator manipulate the integral to isolate dx in terms of du?
-The video creator rewrites the integral to express dx as a function of du by moving terms around and creating a form that can be directly replaced with du or a scalar multiple of du.
What is the new integral expression after applying U-substitution?
-After applying U-substitution, the new integral expression is the integral from 0 to 1 of u times e to the power of u, multiplied by -du.
What are the new bounds for the integral after changing the variable from x to U?
-The new bounds for the integral are when x equals zero (U approaches infinity) and when x equals one (U equals one).
Why does the video creator consider the integral an improper integral?
-The integral is considered improper because one of the bounds goes to infinity, which is not a real number and cannot be directly plugged into the integral.
How does the video creator handle the improper integral with an infinite upper bound?
-The video creator handles the improper integral by rewriting it as a limit as R approaches infinity of the integral from 1 to R of the function.
What method does the video creator use to integrate the function with respect to U?
-The video creator uses the DI method, which is a shorthand for integration by parts, to integrate the function with respect to U.
What is the conclusion of the integration problem in the video?
-The conclusion of the integration problem is that the integral diverges, meaning it approaches positive infinity and does not converge to a finite value.
What is the video creator's goal mentioned in the script?
-The video creator's goal is to reach 10,000 subscribers on their channel and asks viewers to subscribe, like, and share the video to help achieve this goal.
Outlines
📚 Introduction to Integration Problem
The video begins with an introduction to an integration problem involving a quotient function with 'e to the power of one over X' and 'X cubed' in the denominator. The presenter discusses the lack of a quotient rule for integration and suggests the use of substitution methods such as U-substitution or trigonometric substitution. The presenter also mentions the possibility of using integration by parts but decides that U-substitution is more appropriate for this problem. The video includes a call to action for viewers to subscribe and share the video to help the channel reach 10,000 subscribers.
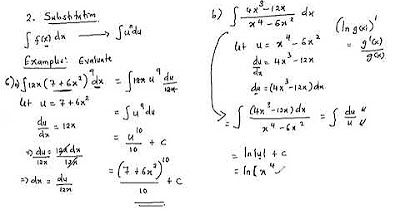
🔍 U-Substitution Process Explained
In this paragraph, the presenter chooses '1 over X' as the substitution variable 'U' and calculates its derivative to find 'dU'. The goal is to rewrite the integral in terms of 'U' and 'dU', isolating 'DX' in the process. The presenter then manipulates the expression to create '1 over X squared' and successfully rewrites the integral in terms of 'U', allowing for the substitution of 'DX' with '-dU'. The integral is now set up for U-substitution, with the expression broken down into components relevant to the chosen substitution variable.
🔄 Adjusting Boundaries for Improper Integral
The presenter addresses the need to adjust the boundaries of the integral due to the change in variables. The new bounds are determined by evaluating 'U' at 'X=0' and 'X=1', resulting in an improper integral with one bound at infinity. The presenter explains the concept of improper integrals and decides to rewrite the integral to handle the infinite upper bound by introducing a real number 'R' that approaches infinity. The integral is then expressed as a limit as 'R' goes to infinity, setting up the stage for the DI method, a form of integration by parts, to be applied.
📉 Conclusion of Integration by Parts
The presenter applies the DI method to the integral, choosing to differentiate 'U' and integrate 'e to the power of U'. The process is repeated until the derivative of 'U' reaches zero, at which point the integration by parts is complete. The final answer is expressed as a limit involving 'R', which when evaluated from 1 to infinity, results in an expression that diverges to positive infinity. The presenter concludes by summarizing the result and encouraging viewers to engage with the content and help the channel reach its subscriber goal.
Mindmap
Keywords
💡Integration
💡Quotient Rule
💡Product Rule
💡U-Substitution
💡Trigonometric Substitution
💡Integration by Parts
💡Improper Integral
💡DI Method
💡Limit
💡Diverges
Highlights
Introduction to an integration problem involving a quotient function with e to the power of 1/X and X cubed.
Discussion on the absence of quotient and product rules for integration, suggesting alternative methods like U-substitution or trigonometric substitution.
The presenter's appeal to subscribers to reach a milestone of 10,000 subscribers and a request for sharing the video.
Choosing 1/X as the substitution variable U and finding its derivative du.
Manipulation of the integral to express dx in terms of du for easier substitution.
Rewriting the integral to match the substitution variable U and expressing dx as a function of du.
Changing the boundaries of the integral from X=0 to X=1 to U=∞ to U=1 after the substitution.
Explanation of improper integrals and the approach to handle boundaries at infinity.
The use of integration by parts, specifically the DI method, for integrating the new expression.
Differentiating U to get a term that simplifies to zero and integrating e^U easily.
Applying the DI method iteratively until reaching a term that can be integrated directly.
Evaluating the integral from 1 to R and taking the limit as R approaches infinity.
The final evaluation of the integral leading to an expression involving e^R and the limit process.
Conclusion that the integral diverges, resulting in positive infinity.
Encouragement for viewers to continue learning and an invitation to like, comment, and share the video.
A reminder of the channel's goal to reach 10,000 subscribers and a call to action for viewer support.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: