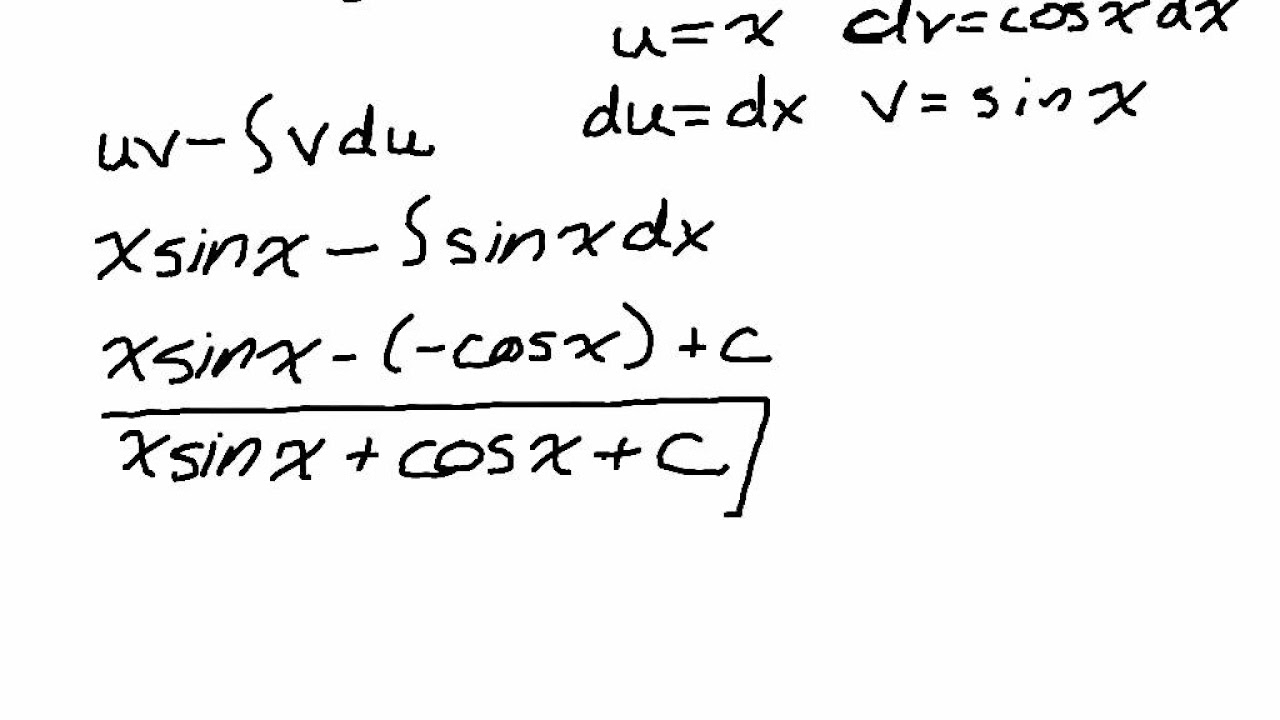Integration by Parts
TLDRThe video script is an educational tutorial on the method of integration known as 'integration by parts.' It begins by presenting the formula for integration by parts, which is integral of u d v equals u v minus integral of v d u. The script then guides viewers through selecting appropriate values for u, dv, du, and v, which are essential for applying the formula. Several examples are provided to illustrate the process, including integrating functions like x cos x and exponential functions. The tutorial also discusses the use of shortcuts for integrating exponential functions and emphasizes that the choice of u and v in integration by parts can vary and is not strictly the first and second terms, respectively. It highlights common choices for u and v, such as inverse trigonometric functions for u and exponential functions for dv. The script concludes with an example of integrating log x, demonstrating the process of choosing u and v and applying the integration by parts formula. The video is designed to help learners understand and apply the integration by parts method effectively.
Takeaways
- 📚 **Integration by Parts Formula**: The integral of u dv is u v minus the integral of v du, which is the core formula used for integration by parts.
- 🔍 **Choosing u and dv**: When applying integration by parts, typically the algebraic term is chosen as 'u', and the trigonometric, exponential, or logarithmic function is chosen as 'dv'.
- 🌟 **Example Application**: The script demonstrates the process of integration by parts using the integral of x cos x dx, showing how to choose u and dv, and how to apply the formula.
- 📉 **Integration of Exponential Functions**: A shortcut for integrating exponential functions involves writing the exponential term as the numerator over its derivative, which simplifies the integration process.
- ✅ **Second Example**: The script shows a second example, integrating x squared times the exponential of 3x, which requires performing integration by parts twice to reach the final answer.
- 🔄 **Repeated Application**: Some integrals may require the process of integration by parts to be repeated multiple times to simplify the expression to an integrable form.
- 📌 **Selection of u and v in Special Cases**: For logarithmic functions, 'u' is chosen as the logarithm, and for inverse trigonometric functions, the inverse trigonometric function is typically taken as 'u'.
- 📐 **Integration of Logarithmic Functions**: When integrating log x, the logarithmic function is taken as 'u', and 'dv' is considered as 1, since the integral of 1 with respect to x is x.
- 🔗 **Substitution in Formula**: After choosing 'u', 'dv', 'du', and 'v', these values are substituted into the integration by parts formula to perform the integration.
- ➗ **Dealing with Constants**: The constant of integration 'c' is added after the final expression is derived, as it accounts for any constant term that may be present in the original integral.
- 🔢 **Final Expression**: The final result of an integral using integration by parts is an expression involving the chosen 'u' and 'v', minus the integral of 'v' times 'du', plus the constant of integration.
Q & A
What is integration by parts?
-Integration by parts is a method used to evaluate integrals. It involves using a specific formula that states the integral of u d v is equal to u v minus the integral of v d u.
What are the four major values needed for integration by parts?
-The four major values needed for integration by parts are u, dv, du (the derivative of u with respect to the variable of integration), and v (the integral of dv with respect to the variable of integration).
How do you choose u and dv for integration by parts?
-u is often chosen as the algebraic term or the term that results in a simpler derivative, while dv is chosen as the function that is easier to integrate. Common choices for u include inverse trigonometric functions and logarithmic functions, while dv is often an exponential or trigonometric function.
What is the formula for integrating exponential functions as a shortcut?
-The shortcut formula for integrating exponential functions is to write the exponential term as the numerator divided by the derivative of the exponent, and keep the exponent as the denominator, then integrate.
How does the integration by parts formula look when applied to the example of x cos x dx?
-For the example of x cos x dx, let u = x and dv = cos x dx. Then du = 1 dx and v = sin x. The formula becomes ∫x cos x dx = x sin x - ∫sin x dx, which simplifies to x sin x + cos x + C, where C is the constant of integration.
What is the process to integrate x^2 * e^(3x) dx using integration by parts?
-First, choose u = x^2 and dv = e^(3x) dx. Then find du = 2x dx and integrate dv to get v = e^(3x)/3. Apply the integration by parts formula to get the result, and you may need to apply integration by parts again to the resulting integral to find the final answer.
How do you integrate log x dx?
-To integrate log x dx, let u = log x and dv = dx. Then du = 1/x dx and v = ∫dx which is x. The integration by parts formula gives ∫log x dx = x log x - ∫x d(log x) = x log x - x + C.
What is the general rule for choosing u and dv when the integral involves a single term like log x?
-When the integral involves a single term like log x, u is chosen as the logarithmic function (log x in this case), and dv is taken as 1 because the integral of 1 with respect to x is x.
Why do we add a constant of integration, C, at the end of an integral solution?
-The constant of integration, C, is added because the integral (antiderivative) of a function represents a family of functions that differ by a constant. The constant of integration accounts for this undetermined constant difference.
Can you always use the first term as u and the second as dv in integration by parts?
-No, the choice of u and dv in integration by parts is not always the first term and the second term, respectively. The choice depends on which function results in a simpler integral or derivative. It's a strategic decision to make the subsequent steps of integration easier.
What happens if you need to apply integration by parts multiple times to solve an integral?
-If an integral requires multiple applications of integration by parts, you would repeat the process, using the result of one integration by parts as the new integral to evaluate in the subsequent step. This can happen when the integral does not simplify to a standard form after the first application.
Outlines
📚 Introduction to Integration by Parts
This paragraph introduces the concept of integration by parts, a method for integrating functions of the form u*dv. The formula for integration by parts is presented as ∫u dv = u*v - ∫v du. The speaker outlines the four key values needed for this method: u, dv, du, and v, and provides an example using the integral of x*cos(x) dx. The process involves choosing u and dv, differentiating u to find du, and integrating dv to find v, and then substituting these into the formula to solve the integral.
🔢 Applying Integration by Parts to Exponential Functions
The second paragraph delves into applying integration by parts to exponential functions. It demonstrates the use of substitution by setting u = 3x, which simplifies the integral of e^(3x). The process involves differentiating u to find du and integrating dv to find v, then applying the integration by parts formula. A shortcut for integrating exponential functions is also discussed, which involves taking the exponential's coefficient as the numerator and the derivative of the exponential's argument as the denominator, then adding the constant of integration.
🧮 Advanced Integration by Parts with Exponential Functions
This paragraph showcases a more complex example of integration by parts involving x^2 * e^(3x). The speaker chooses u = x^2 and dv = e^(3x), then finds du and v accordingly. The integration by parts formula is applied, and since the result still contains an integral of the same form, a second round of integration by parts is performed. The process is iterative, highlighting the need to reapply the method until the integral can be expressed in a final form.
🔁 Revisiting Integration by Parts with Trigonometric Functions
The fourth paragraph revisits integration by parts with a focus on the integral of x*cos(x) dx. It emphasizes that the order of u and v is not fixed and depends on the function being integrated. The speaker clarifies that in some cases, u could be the second term and v the first, challenging the assumption that u is always the first term.
📉 Choosing u and v in Integration by Parts
The fifth paragraph discusses the strategy for choosing u and dv in integration by parts. It suggests that u is often an inverse trigonometric function, logarithmic function, or algebraic function, while dv is typically an exponential function or trigonometric function. The speaker provides a rule of thumb for selecting u and dv based on the types of functions involved in the integral.
📈 Integrating Logarithmic Functions by Parts
The final paragraph deals with integrating a logarithmic function, log(x), using the method of integration by parts. Since there is only one term, the integral is rewritten as log(x) * 1 to fit the u*dv format. The speaker assigns u = log(x) and dv = 1, finds du and v, and then applies the integration by parts formula. The result is x*log(x) - x, plus the constant of integration, demonstrating how to handle a single-term integral in this context.
Mindmap
Keywords
💡Integration by parts
💡Integration formula
💡Definite integral
💡Antiderivatives
💡Exponential functions
💡Logarithmic functions
💡Trigonometric functions
💡Constants of integration
💡Differentiation
💡Integration by substitution
💡Inverse trigonometric functions
Highlights
Introduction to integration by parts, a method for integral evaluation using a specific formula.
The formula for integration by parts is ∫udv = uv - ∫vdu.
Four major values are required for integration by parts: u, du, v, and dv.
Example given to demonstrate the process: ∫x cos x dx.
Selection of u and dv for the integral ∫x cos x dx, where u = x and dv = cos x.
Differentiating u to find du and integrating dv to find v, resulting in du = 1 and v = sin x.
Substituting values into the integration by parts formula to solve the integral.
Result of the first example: x sin x - sin x + C, where C is the constant of integration.
Integration by substitution is used for exponential functions, demonstrated with ∫e^(3x) dx.
Shortcut for integrating exponential functions: (e^u)/(u) + C, where u is the differentiated part.
Applying the shortcut to integrate x^2 e^(3x) dx using integration by parts.
Performing a second round of integration by parts for the remaining integral in the solution.
Final answer for the integral of x^2 e^(3x) dx after applying integration by parts twice.
Discussion on choosing u and v in integration by parts, with u often being the algebraic term and v the trigonometric or exponential term.
Integration by parts does not always mean u is the first term and v is the second; the order can be switched.
Logarithmic functions are typically chosen as u when using integration by parts.
Integration of log x dx by treating log x as u and 1 as dv, resulting in x log x - x + C.
Integration by parts can sometimes require multiple iterations to reach the final solution.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: