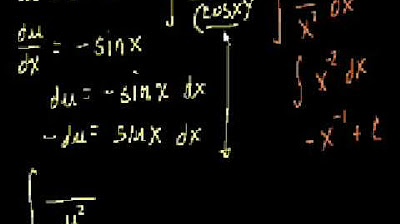Math olympiad Integral

Math with Marker
1 Dec 202303:46
EducationalLearning
32 Likes 10 Comments

TLDRIn this video, the host guides viewers through solving an intriguing integral problem from the MTH Olympiad in Brooklyn. By introducing a substitution method, where 'a^x' is replaced with 'T', the complex integral simplifies to a more manageable form. The host then demonstrates a second substitution, transforming the integral into 'e^U * dU', which is easily solvable. The final answer, 'e^(e^x)', is elegantly derived, showcasing the beauty of mathematical problem-solving. The video encourages viewers to subscribe and like for more such content.

Takeaways
  • 📚 The video discusses an integral problem from the MTH Olympiad, a mathematics competition.
  • 🔍 The integral given is ∫ from 0 to 1 of e^x * a^(x * a) * a^(e^x) dx, where 'a' is a constant.
  • 📝 A substitution method is introduced to simplify the integral, setting a^x as 'T'.
  • 🧐 The derivative of e^x * dx is equated to dT, which simplifies the integral to involve 'T' instead of 'x'.
  • 📈 The function e^x is differentiated with respect to 'T', resulting in e^T * dT, which is then equated to du.
  • 🌟 The integral is then transformed into an easier form, ∫e^U * dU, where U is e^T.
  • 💡 The integral of e^U * dU is solved as e^(e^U), which simplifies to e^(e^(e^x)) after substituting back for 'U' and 'T'.
  • 📉 The limits of integration are applied, with the result being e^e evaluated from 0 to 1.
  • 🎯 The final answer to the integral is e^e, which is a significant mathematical constant.
  • 👍 The video encourages viewers to subscribe, like, and watch for more content.
Q & A

  • What is the topic of the video?

    -The video discusses a solution to a specific integral problem from the MTH Olympiad, a math tournament in Brooklyn.

  • What is the integral given in the video?

    -The integral is from 0 to 1 of e^x times a^(a^x) * a^(e^x) dx.

  • What substitution is made to simplify the integral?

    -The substitution made is to let a^x = T, which simplifies the integral by changing the variable from x to T.

  • How is the derivative of a function a^u related to u' and a?

    -The derivative of a function y = a^u is y' = u' * ln(a) * a^u, where u' is the derivative of u with respect to x.

  • What happens when a is set to e in the derivative formula?

    -When a is set to e, the derivative of the function becomes u' * e^u, simplifying the expression since e is the base of the natural logarithm.

  • What substitution is made after rewriting e^x as T?

    -After rewriting e^x as T, the substitution made is to let e^T = U, which further simplifies the integral by changing the variable from T to U.

  • What is the final form of the integral after all substitutions?

    -The final form of the integral is the integral of e^U with respect to U, which is a straightforward exponential integral.

  • What is the result of the integral after evaluating it from 0 to 1?

    -The result of the integral is e^(e^(e)), which is obtained by evaluating the integral from 0 (where U = 1) to 1 (where U = e).

  • What is the significance of the final answer e^(e^(e))?

    -The final answer e^(e^(e)) is a beautiful and elegant result that showcases the power of mathematical transformations and substitutions in solving complex integrals.

  • What does the video recommend for viewers who enjoyed the content?

    -The video recommends that viewers who enjoyed the content should subscribe to the channel, like the video, and watch more similar content.

  • What is the main teaching point of the video?

    -The main teaching point of the video is to demonstrate the process of solving a complex integral problem using substitution and the properties of derivatives.

Outlines
00:00
📚 Solving an MTH Olympiad Integral Problem

This paragraph introduces a problem from the Brooklyn Math Olympiad, involving the integral from 0 to 1 of e^x * a^(a^x) dx. The speaker simplifies the problem by substituting a^x with T and differentiating accordingly. The process involves using the chain rule for differentiation and simplifying the integral to e^T dT, which is then solved to find the final answer e^(e^x) evaluated from 0 to 1, resulting in e^e - 1. The speaker encourages viewers to subscribe and like the video for more content.

Mindmap
Keywords
💡Integral
An integral is a fundamental concept in calculus, representing the area under the curve of a function over a given interval. In the video, the integral is used to solve a complex problem involving exponential functions. The script discusses the integral from 0 to 1 of the function e^(x) * a^(ax) * e^(-x)dx, which is the main focus of the problem-solving process.
💡Derivative
The derivative is a mathematical operation that gives the rate at which a function is changing at any given point. In the context of the video, the derivative is used to transform the integral into a simpler form by recognizing that the derivative of e^(x) * dx is equal to dT when T is defined as a^(x).
💡Exponential Function
An exponential function is a mathematical function where the variable is in the exponent. In the video, the script involves multiple exponential functions, such as e^(x) and a^(x), which are manipulated to simplify the integral and find the solution.
💡Substitution
Substitution is a common technique in calculus used to simplify an integral by replacing a part of the integrand with a new variable. The video demonstrates this by setting T = a^(x), which simplifies the integral and makes it easier to solve.
💡Differentiation
Differentiation is the process of finding the derivative of a function. The video script uses differentiation to express e^(x) * dx as dT when T is a new variable representing a^(x), which is a key step in solving the integral.
💡Natural Logarithm
The natural logarithm, often denoted as ln, is the logarithm to the base e. In the script, the natural logarithm is mentioned in the context of the derivative of a^(u), where the derivative is u' * ln(a), with a being e.
💡Chain Rule
The chain rule is a fundamental theorem in calculus for differentiating composite functions. It is implicitly used in the video when the derivative of a^(x) is expressed in terms of e^(u), where u is a new variable.
💡Simplifying an Integral
Simplifying an integral involves transforming a complex integral into a more manageable form. The video demonstrates this by using substitution and differentiation to simplify the original integral into an exponential function that can be easily integrated.
💡Euler's Number (e)
Euler's number, denoted as 'e', is an important mathematical constant approximately equal to 2.71828. It is the base of the natural logarithm and is used extensively in the video's integral problem as the base of the exponential functions.
💡Power Function
A power function is a function of the form f(x) = x^n, where n is a constant. In the video, power functions are used in the form of a^(x) and e^(x), which are integral to the problem and its solution.
💡Final Answer
The final answer in a mathematical problem is the solution after all steps have been correctly executed. In the context of the video, the final answer to the integral problem is e^(e), which is derived through a series of steps involving substitution and simplification.
Highlights

Introduction to the MTH Olympiad problem from Brooklyn Mass tournament.

Presenting a complex integral problem involving exponential functions.

Simplifying the integral by substituting a^x with T.

Differentiating the left side to find the relationship between e^x * dx and dT.

Deriving the derivative of a function with base 'a' raised to a variable 'U'.

Applying the derivative to the specific case where 'a' is equal to 'e'.

Transforming the integral by substituting e^T for the exponential term.

Further simplification by integrating e^U * dU.

Recognizing the integral of e^U as e^U.

Substituting back the original variables to find the solution.

Calculating the final answer by evaluating the integral from 0 to 1.

Arriving at the final answer of e^e as the solution to the integral.

Encouraging viewers to subscribe and like the video for more content.

Expressing gratitude for watching the video and engaging with the content.

Highlighting the beauty of the mathematical solution obtained.

The process of solving the integral involves multiple substitutions and simplifications.

The integral problem showcases the application of derivatives in solving complex integrals.

The final solution demonstrates the exponential function's unique properties.

Transcripts

Browse More Related Video

Lesson 11 - Integration By Substitution (Calculus 1 Tutor)

Another u-subsitution example

Integration Of Exponential Functions [ Substitution Method ]

Definite Integral With U-Substitution

Integration by Substitution

_-substitution: logarithmic function | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Math OlympiadIntegral SolutionBrooklynEducationalMathematicsE^xDerivativeCalculusTournamentProblem Solving