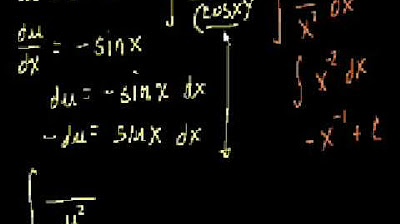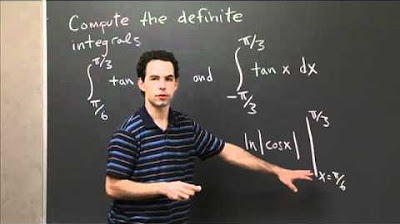Antidifferentiation by substitution | MIT 18.01SC Single Variable Calculus, Fall 2010
TLDRIn this recitation, the professor introduces three antiderivatives to compute, focusing on integration by substitution and 'advanced guessing'. The first problem involves a nested function, e^(2x)cos(1-e^(2x)), tackled with a u-substitution. The second problem, 4x(5x^2-1)^(1/3), is solved using advanced guessing, correcting for a constant discrepancy. The third problem, tan(x)dx, is transformed into sin(x)/cos(x) and integrated by substituting u=cos(x), resulting in a logarithmic antiderivative. The session concludes with a demonstration of these integration techniques.
Takeaways
- 📚 The lecture focuses on antidifferentiation, specifically using substitution and 'advanced guessing' methods.
- 🔍 Three antiderivatives are presented for computation: e^(2x)cos(1 - e^(2x)), 4x(5x^2 - 1)^(1/3), and tan(x)dx.
- 🧐 The first problem is tackled using substitution, with u = 1 - e^(2x), simplifying the integral to involve the cosine function.
- 📉 The substitution for the first problem leads to an integral in terms of u, which is then solved using the antiderivative of cosine, resulting in -1/2sin(u).
- 🔄 After solving the first integral, the substitution is reversed to express the antiderivative in terms of the original variable x.
- 🤔 The second problem is approached with 'advanced guessing', assuming the integral of a polynomial raised to a power can be derived from a similar expression.
- 📈 The integral of 4x(5x^2 - 1)^(1/3) is solved by correcting a guessed expression, resulting in (3/10)(5x^2 - 1)^(4/3).
- 📝 For the third problem, the integral of tan(x) is rewritten in terms of sine and cosine, allowing for a substitution that simplifies the integral.
- 🔑 The substitution u = cos(x) for the third problem leads to an integral in terms of u, which is solved using the natural logarithm function.
- 📚 The antiderivative of tan(x) is found to be -ln(|cos(x)|), which is consistent with previous findings on the derivative of ln(cos(x)) being -tan(x).
- 🎓 The lecture concludes with a demonstration of antidifferentiation techniques, emphasizing the importance of recognizing patterns and making educated guesses.
Q & A
What is antidifferentiation?
-Antidifferentiation, also known as integration, is the process of finding the antiderivative of a function, which is the reverse of differentiation.
What is the first antiderivative problem presented in the script?
-The first antiderivative problem is to find the antiderivative of \( e^{2x} \cos(1 - e^{2x}) \, dx \).
What substitution method is suggested for the first problem?
-For the first problem, the substitution \( u = 1 - e^{2x} \) is suggested, which simplifies the integral by making it easier to integrate the cosine function.
How is the substitution \( du = -2e^{2x} \, dx \) derived from the substitution \( u = 1 - e^{2x} \)?
-By differentiating \( u = 1 - e^{2x} \) with respect to \( x \), we get \( du = -2e^{2x} \, dx \), which is used to transform the integral into a form that involves \( u \) instead of \( x \).
What is the antiderivative of the cosine function?
-The antiderivative of the cosine function is the sine function, which means that the integral of \( \cos(u) \) with respect to \( u \) is \( \sin(u) \) plus a constant.
How is the second antiderivative problem approached in the script?
-The second antiderivative problem, involving \( 4x(5x^2 - 1)^{1/3} \, dx \), is approached using advanced guessing, which involves rewriting the expression to match the form of a known derivative.
What is 'advanced guessing' in the context of antidifferentiation?
-Advanced guessing is a method in antidifferentiation where one rewrites the integral in a form that resembles the derivative of a known function, allowing for easier integration.
What is the third antiderivative problem presented in the script?
-The third antiderivative problem is to find the antiderivative of \( \tan(x) \, dx \).
What substitution is used for the integral of \( \tan(x) \) in the script?
-For the integral of \( \tan(x) \), the substitution \( u = \cos(x) \) is used, which leads to \( du = -\sin(x) \, dx \) and simplifies the integral to \( -\int \frac{1}{u} \, du \).
What is the antiderivative of \( \frac{1}{u} \) with respect to \( u \)?
-The antiderivative of \( \frac{1}{u} \) with respect to \( u \) is the natural logarithm of the absolute value of \( u \), which is \( -\ln|u| + C \) where \( C \) is the constant of integration.
How does the script relate the antiderivative of \( \tan(x) \) to the derivative of \( \ln(\cos(x)) \)?
-The script relates the antiderivative of \( \tan(x) \) to the derivative of \( \ln(\cos(x)) \) by showing that the derivative of \( \ln(\cos(x)) \) is \( -\tan(x) \), which is the original function to be integrated.
Outlines
📚 Antidifferentiation Techniques
The professor introduces the topic of antidifferentiation, focusing on integration by substitution and a method known as 'advanced guessing'. They present three antiderivatives to solve: the first involving an exponential and trigonometric function, the second a polynomial raised to a power, and the third the tangent function. The professor encourages students to attempt these problems before discussing the solutions.
🧠 Solving Antiderivatives with Substitution and Advanced Guessing
The professor explains the process of solving the first antiderivative using substitution, where they let u equal 1 minus e to the 2x, transforming the integral and simplifying it to the antiderivative of a cosine function. For the second problem, the professor uses advanced guessing, recognizing a pattern that resembles a derivative and adjusting for the constant discrepancy to find the antiderivative. The third problem involves rewriting the tangent function in terms of sine and cosine and using a substitution where u equals cosine x, leading to the natural logarithm function as the antiderivative. The professor concludes with a brief mention of a previous recitation where the derivative of the natural logarithm of cosine x was discussed.
📖 Conclusion of Antidifferentiation Discussion
The script ends with a concluding paragraph that does not contain specific content but implies that the professor is wrapping up the lesson on antidifferentiation, possibly preparing to move on to the next topic or allowing students to reflect on the material covered.
Mindmap
Keywords
💡Antidifferentiation
💡Integration by substitution
💡Advanced guessing
💡Nested function
💡Derivative
💡Chain rule
💡Polynomial
💡Sine and Cosine
💡Logarithm
💡Constant of integration
💡Tangent function
Highlights
Introduction to antidifferentiation and integration methods discussed in the recitation.
Problem 1: Antiderivatives of e^(2x) * cos(1 - e^(2x)) dx.
Suggestion to try computing antiderivatives before the solution is presented.
Problem 2: Antiderivatives of 4x * (5x^2 - 1)^(1/3).
Problem 3: Antiderivatives of tan(x) dx.
Substitution method for the first problem using u = 1 - e^(2x).
Derivative du = -2e^(2x) dx used for substitution.
Integration of cos(u) resulting in -1/2 * sin(u) + C after substitution.
Re-substitution to express the antiderivative in terms of x.
Advanced guessing method for the second problem involving a power rule.
Derivative of (5x^2 - 1)^(4/3) leads to the integral form.
Correction of constants by multiplying by 3/10 to match the integral.
Rewriting tan(x) as sin(x)/cos(x) for the third problem.
Substitution u = cos(x) for the integral of sin(x)/cos(x).
Integration resulting in -ln|u| + C, then substituting back for x.
Connection to previous work on the derivative of ln(cos(x)) = -tan(x).
Summary of antidifferentiation techniques using substitution and advanced guessing.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: