Physics 53 Polarization (2 of 5) Two Polarizers

Michel van Biezen
29 Apr 201303:47
EducationalLearning
32 Likes 10 Comments

TLDRThis educational script explains the concept of light intensity through polarizers. It starts by stating that light loses half its intensity after passing through the first polarizer. The script then introduces a formula to calculate the intensity after a second polarizer, which depends on the angle between the two. Using 30° as an example, it shows that the light's intensity is further reduced to 37.5% of the original. Finally, it illustrates the total blockage of light when the second polarizer is perpendicular to the first, demonstrating the principle behind polarization in sunglasses.

Takeaways
  • 🔆 The intensity of light passing through the first polarizer is reduced to half of its original intensity.
  • 📏 The intensity after the second polarizer is calculated using the formula \( I_2 = I_1 \times \cos^2(\Theta_1) \), where \( \Theta_1 \) is the angle between the polarizers.
  • 📐 When the second polarizer is at a 30° angle to the first, the intensity through the second is \( 0.75 \times I_1 \).
  • 🔄 The intensity after the second polarizer can be further expressed as \( I_2 = 0.375 \times I_0 \), where \( I_0 \) is the original intensity.
  • 🕶️ If the second polarizer is perpendicular (90°) to the first, no light passes through, as the cosine of 90° is zero.
  • 👓 Demonstrating with polarized sunglasses, holding one pair perpendicular to another shows no light transmission.
  • 🌟 The principle of polarization is effectively used in sunglasses to reduce glare and improve visual comfort.
  • 📉 The intensity loss through polarizers is cumulative and depends on the angle between them.
  • 📚 Understanding the angle between polarizers is crucial for predicting the transmitted light intensity.
  • 📈 The script provides a step-by-step example to illustrate the calculation of light intensity through polarizers.
  • 🔬 The concept is applicable in various scenarios, including optics and everyday items like sunglasses.
Q & A

  • What happens to the intensity of light when it passes through the first polarizer?

    -The intensity of light is reduced to half of its original value when it passes through the first polarizer.

  • How do you calculate the intensity of light after it passes through a second polarizer that is at an angle to the first one?

    -The intensity of light after passing through the second polarizer is calculated using the equation I2 = I1 * cos²(θ), where θ is the angle between the first and second polarizers.

  • What is the intensity of light after passing through two polarizers if the second polarizer is at a 30° angle relative to the first?

    -If the second polarizer is at a 30° angle relative to the first, the intensity of light passing through the second polarizer is 37.5% of the original intensity.

  • Why is the intensity reduced to 37.5% when the angle between the polarizers is 30°?

    -The reduction to 37.5% occurs because the light's intensity after passing through the second polarizer is determined by the cosine squared of the angle between the polarizers, which for 30° is cos²(30°) = 0.75.

  • What happens to the intensity of light if the second polarizer is perpendicular (90°) to the first one?

    -If the second polarizer is perpendicular (90°) to the first one, no light passes through, resulting in zero intensity.

  • Why does no light pass through when the polarizers are at 90° to each other?

    -No light passes through because the cosine of 90° is zero, and since the intensity depends on cos²(θ), the intensity becomes zero when the polarizers are perpendicular.

  • What practical example is given to demonstrate the effect of perpendicular polarizers?

    -A practical example given is using two pairs of polarized sunglasses. When one is held upright and the other perpendicular, no light passes through, demonstrating the effect of perpendicular polarizers.

  • How is the concept of polarization useful in real-life applications?

    -Polarization is useful in applications like polarized sunglasses, which reduce glare by blocking certain orientations of light waves.

  • What additional scenarios are mentioned for future examples in the script?

    -The script mentions future examples where polarizers will be placed at various angles relative to each other, and more than two polarizers will be used to explore the effects.

  • How does the script suggest verifying the effect of perpendicular polarizers at home?

    -The script suggests using two pairs of polarized sunglasses, positioning one pair upright and the other perpendicular, to observe that no light passes through.

Outlines
00:00
🔬 Calculating Light Intensity Through Polarizers

This paragraph explains the process of calculating the intensity of light that passes through two polarizers oriented at different angles. It begins by stating that the first polarizer reduces the light's intensity by half. The second polarizer's effect is then calculated using the formula I₂ = I₁ * cos²(θ), where θ is the angle between the polarizers. The example given uses a 30° angle, resulting in a further reduction to 37.5% of the original intensity. The paragraph also discusses the scenario where the second polarizer is perpendicular (90°) to the first, which would block all light. The explanation includes practical examples, such as using polarized sunglasses, to illustrate the concept.

Mindmap
Keywords
💡Intensity of Light
The intensity of light refers to the amount of light energy passing through a unit area at a given time. In the context of the video, it is crucial for understanding how much light is transmitted through polarizers. The script explains that the intensity of light is halved after passing through the first polarizer, setting the stage for further calculations involving the second polarizer.
💡Polarizers
Polarizers are optical filters that allow light waves to pass through in a specific orientation. The video script discusses two polarizers, one aligned vertically and the other at a 30-degree angle to the first, to illustrate how the orientation affects the light's intensity. Polarizers play a central role in the video's theme of light polarization and its manipulation.
💡Angle
The angle in the script is the measure of the orientation difference between the two polarizers. It is essential for calculating the intensity of light after passing through both polarizers. The script uses a 30-degree angle to demonstrate the relationship between the angle and the light's intensity, showing that the angle affects the amount of light transmitted.
💡Cosine Square
The cosine square is a mathematical function used in the script to calculate the intensity of light after it passes through the second polarizer. It is the square of the cosine of the angle between the polarizers. The script mentions that the intensity of light after the second polarizer is I1 times the cosine square of the angle, illustrating the direct mathematical relationship between angle and light intensity.
💡Original Intensity
Original intensity refers to the intensity of light before it encounters any polarizers. The script uses this term to compare the light's intensity at different stages of passing through the polarizers. It is a baseline for understanding the reduction in light intensity as it interacts with the polarizers.
💡I sub 1 and I sub 2
In the script, I sub 1 and I sub 2 represent the intensities of light after passing through the first and second polarizers, respectively. These terms are used to denote the sequential reduction in light intensity as it passes through each polarizer. They are key to understanding the script's explanation of how light intensity changes with each interaction.
💡Percentage
Percentage is used in the script to express the final intensity of light as a proportion of the original intensity. It helps to quantify the loss of light intensity in a more relatable way. The script concludes that I sub 2 is 37.5% of the original intensity, providing a clear and understandable measure of the light's reduction.
💡Perpendicular
Perpendicular in the script refers to the orientation of the second polarizer being at a 90-degree angle to the first. This orientation is used to illustrate a scenario where no light passes through the second polarizer, as the cosine of 90 degrees is zero, indicating complete blockage of light.
💡Polarized Sunglasses
Polarized sunglasses are mentioned in the script as a real-world application of polarizers. They are used to demonstrate the practical effect of polarizers when held perpendicular to each other, blocking all light. This example helps viewers understand the concept of polarization in a familiar context.
💡Light Waves
Light waves are the oscillating electric and magnetic fields that propagate through space, carrying energy. In the script, the orientation of these waves is manipulated by polarizers to control the intensity of light. The concept of light waves is fundamental to understanding how polarizers work and affect light transmission.
Highlights

The process of calculating light intensity through polarizers is explained step by step.

Intensity after the first polarizer (I1) is half of the original intensity (I0).

The equation for calculating intensity after the second polarizer (I2) is I2 = I1 * cos²(θ), where θ is the angle between the polarizers.

When the second polarizer is at a 30° angle to the first, the intensity loss is calculated using cos²(30°).

Cosine of 30° squared results in 0.75, indicating the intensity after the second polarizer is 75% of the intensity after the first.

I2 is expressed as 0.375 times I0, showing a 62.5% intensity reduction from the original.

If the second polarizer is perpendicular (90°) to the first, no light passes through, as cos(90°) is zero.

Demonstrates the practical application of polarizers with an example of sunglasses blocking light when crossed.

Explains the principle behind polarization and its effectiveness in blocking light at perpendicular angles.

The transcript includes further examples of polarizers at various angles to explore light transmission.

The importance of angle θ in determining the intensity of light passing through multiple polarizers is emphasized.

The mathematical relationship between polarizer angles and light intensity is clearly outlined.

The concept of light losing intensity with each polarizer is introduced and explained.

The transcript provides a clear understanding of how polarizers work in pairs to control light intensity.

The impact of polarizer orientation on light transmission is thoroughly discussed.

A real-world analogy of polarized sunglasses is used to illustrate the concept of light blocking.

The transcript concludes with a mention of additional examples to further understand polarizer interactions.

Transcripts

Browse More Related Video

The Polarizer | Physics with Professor Matt Anderson | M28-17

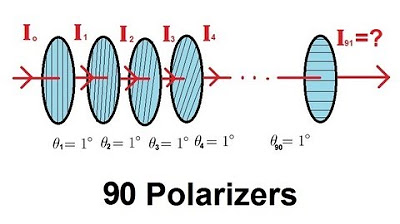
Physics 53 Polarization (4 of 5) Ninety Polarizers

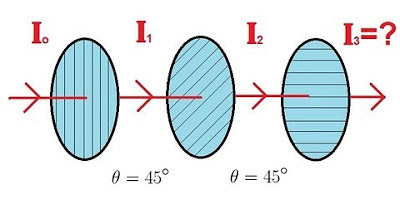
Physics 53 Polarization (3 of 5) Three Polarizers

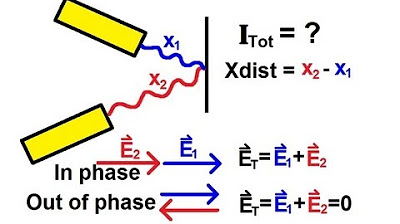
Physics 60 Interference of Light (1 of 8) Path and Phase Difference: Introduction

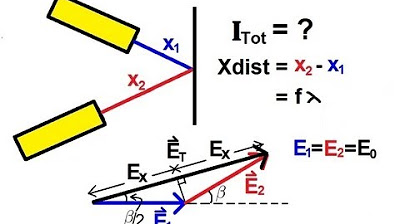
Physics 60 Interference of Light (3 of 8) Path and Phase Difference: General Case

Physics 60 Interference of Light (2 of 8) Path and Phase Difference

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PolarizationLight IntensityOpticsCosine LawPolarizersAngle EffectPhysicsEducationalScienceExperiment