How to Use the Z Table

Kari Alexander
9 Jun 201304:58
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explains the use of the Z-table in statistics, focusing on the concept of p-values. It clarifies that p-values represent the proportion of observations to the right of a specific Z-score, illustrating this with a graph and table. The script details how to locate a Z-score in the table to find the corresponding p-value, using the first two digits for the column and the third for the row. It emphasizes the table's symmetry, indicating that p-values for positive and negative Z-scores of the same magnitude are equal, providing an example with Z = 1.23 and its p-value of 0.1093.

Takeaways
  • 📊 The Z table is divided into two sections: a graph/chart and a table that lists possible p-values.
  • 🔢 A p-value represents the proportion of observations that are to the right of a specific Z-score.
  • 🎯 P-values can be interpreted as probabilities or proportions of all possible values beyond a certain point.
  • 📈 The Z table provides the proportion of observations to the right of a given Z-score across a standard normal distribution.
  • 🔍 To find a p-value, locate the Z-score in the table by matching the first two digits in the left column and the third digit in the top row.
  • 🌐 The Z table is symmetrical, meaning the p-value for Z and -Z is the same, reflecting the properties of a normal distribution.
  • 🔑 The p-value at Z = 1.23 is given as 0.1093, indicating 10.93% of observations are to the right of this Z-score.
  • 📚 The table is used by looking up a specific Z-score to determine the proportion of data that falls beyond it.
  • 📉 The concept of p-values is crucial for understanding statistical significance in hypothesis testing.
  • 📝 Remembering the structure of the Z table is essential for correctly interpreting and using p-values in statistical analysis.
  • 📉 Understanding p-values helps in determining the likelihood of observing a particular result under the null hypothesis.
Q & A

  • What are the two sections of the Z table?

    -The Z table consists of a graph or chart at the top and a table at the bottom. The graph represents the distribution, while the table provides numerical values related to Z-scores.

  • What is a p-value in the context of the Z table?

    -A p-value is the proportion of observations that are to the right of a specific Z-score. It can be thought of as a probability or a proportion of all possible values.

  • How can you interpret a p-value?

    -A p-value can be interpreted in two ways: as the probability that a randomly selected observation will fall in a certain range, or as the proportion of all observations that fall beyond a specific point.

  • Where do the p-values in the Z table come from?

    -The p-values come from the Z table itself, which provides the proportion of observations to the right of each possible Z-score across the distribution.

  • How is the Z distribution symmetrical as mentioned in the script?

    -The Z distribution is symmetrical because for every positive Z-score, there is a corresponding negative Z-score with the same p-value. For example, Z = 1.23 and Z = -1.23 both have the same p-value.

  • How do you find the p-value for a specific Z-score using the Z table?

    -To find the p-value for a specific Z-score, look up the first two digits of the Z-score in the left column and the third digit in the top row of the table to find the corresponding p-value.

  • What does the gray area in the script represent?

    -The gray area represents the range of observations that are to the right of a specific Z-score, which corresponds to the p-value for that Z-score.

  • What is the p-value for Z = 1.23 according to the script?

    -The p-value for Z = 1.23 is 0.1093, which means 10.93% of observations are to the right of Z = 1.23 in the distribution.

  • Why is it important to understand the Z table?

    -Understanding the Z table is important for statistical analysis, as it helps in determining the probability or proportion of observations beyond a certain point, which is crucial for hypothesis testing and data interpretation.

  • Can the Z table be used for both positive and negative Z-scores?

    -Yes, the Z table can be used for both positive and negative Z-scores due to the symmetry of the distribution, with the p-value being the same for Z and -Z.

  • What is the significance of the Z-score of 0 in the distribution?

    -A Z-score of 0 represents the mean of the distribution. Half of the data lies above this point, and the other half lies below it, making it a central reference point in the distribution.

Outlines
00:00
📊 Understanding the Z Table and P Values

This paragraph explains the structure and usage of the Z table in statistics. It consists of a graphical representation and a numerical table. The table provides possible p-values, which are the proportions of observations to the right of specific Z-scores. A p-value can be interpreted as the probability of selecting a random Z value that falls within a certain range or as the proportion of all possible values that exceed a specific point. The Z table is used to find the p-value for a given Z-score by locating the first two digits in the leftmost column and the third digit in the top row. The paragraph also emphasizes the symmetry of the Z distribution, indicating that the p-value for Z and -Z is the same.

Mindmap
Keywords
💡Z table
The Z table is a statistical tool used to determine the probability or proportion of observations that fall beyond a certain point in a standard normal distribution. In the video, the Z table is introduced as a two-part tool with a graph and a table, where the table lists possible p-values for various Z-scores. The script explains how to use the Z table to find the p-value for a given Z-score, which is central to understanding the theme of the video.
💡p-value
A p-value is a statistical measure that represents the probability of obtaining results at least as extreme as the observed results, assuming that the null hypothesis is true. In the video, the p-value is described as both a probability and a proportion of observations to the right of a specific Z-score. The script uses the p-value to illustrate how to interpret data in relation to the Z table.
💡Z-score
A Z-score, also known as a standard score, is a measure of how many standard deviations an element is from the mean. The video script explains that the Z table includes Z-scores ranging from 0, which is the mean of the distribution, to various positive and negative values. Each Z-score corresponds to a p-value, indicating the proportion of observations beyond that score.
💡Observations
In statistics, observations refer to the data points collected during an experiment or study. The video script discusses how the Z table can be used to determine the proportion of observations that fall to the right of a specific Z-score, emphasizing the importance of understanding the distribution of data points.
💡Distribution
A distribution in statistics refers to the way data points are spread out. The video script mentions a standard normal distribution, which is symmetrical and centered around the mean (Z = 0). The Z table helps in understanding the distribution by providing p-values for different Z-scores.
💡Graph
The term 'graph' in the script refers to the visual representation of the data distribution, likely a bell curve, which is part of the Z table. The graph helps in visually understanding the distribution of Z-scores and their corresponding p-values.
💡Table
The 'table' mentioned in the script is the tabular part of the Z table that lists the p-values for different Z-scores. It is used to look up the proportion of observations that are to the right of a specific Z-score.
💡Symmetric
The script points out that the standard normal distribution is symmetrical, meaning that the proportion of observations to the left of a Z-score is the same as the proportion to the right of its negative counterpart. This symmetry is important for understanding the balance in data distribution.
💡Proportion
In the context of the video, proportion refers to the part of the total number of observations that fall into a certain category, such as being to the right of a Z-score. The script explains how to interpret the p-value as a proportion using the Z table.
💡Probability
Probability in the script is used to describe the likelihood of selecting an observation that falls into a specific range when randomly choosing from the distribution. The p-value is also described as a probability, indicating the chance that an observation will be to the right of a given Z-score.
💡Mean
The mean, or average, is a central value in a data set. In the standard normal distribution discussed in the video, the mean is 0, and Z-scores are calculated based on how many standard deviations away from this mean a particular observation is.
Highlights

Introduction to the Z table and its two main sections: a graph/chart and a table.

Explanation of p-values as the proportion of observations to the right of specific Z scores.

Interpreting p-values as both a probability and a proportion.

Description of the gray area in the graph representing the p-value.

Origin of p-values from the Z table.

Distribution of Z scores across the graph with Z equals 0 at the center.

How to find the proportion of observations to the right of a specific Z score using the table.

Method to locate Z scores in the table using the first two and third digits.

Example of looking up the p-value for Z = 1.23 and finding it to be 0.1093.

Explanation of the symmetrical nature of the Z table and p-values.

Demonstration of finding the p-value for Z = -1.23, which is the same as for Z = 1.23.

Emphasis on the importance of understanding p-values as they relate to the Z table.

Clarification that p-values are found inside the table with corresponding Z scores.

Instruction on how to use the left column and top row to find the correct p-value.

Highlighting the table's symmetry and its implications for Z scores.

Final summary of the process for using the Z table to find p-values.

Transcripts

Browse More Related Video

Normalized Table: Understand z scores, p values, critical values

How to find critical Z value (Z alpha)

P Values, z Scores, Alpha, Critical Values

How To Find The Z Score Given The Confidence Level of a Normal Distribution 2

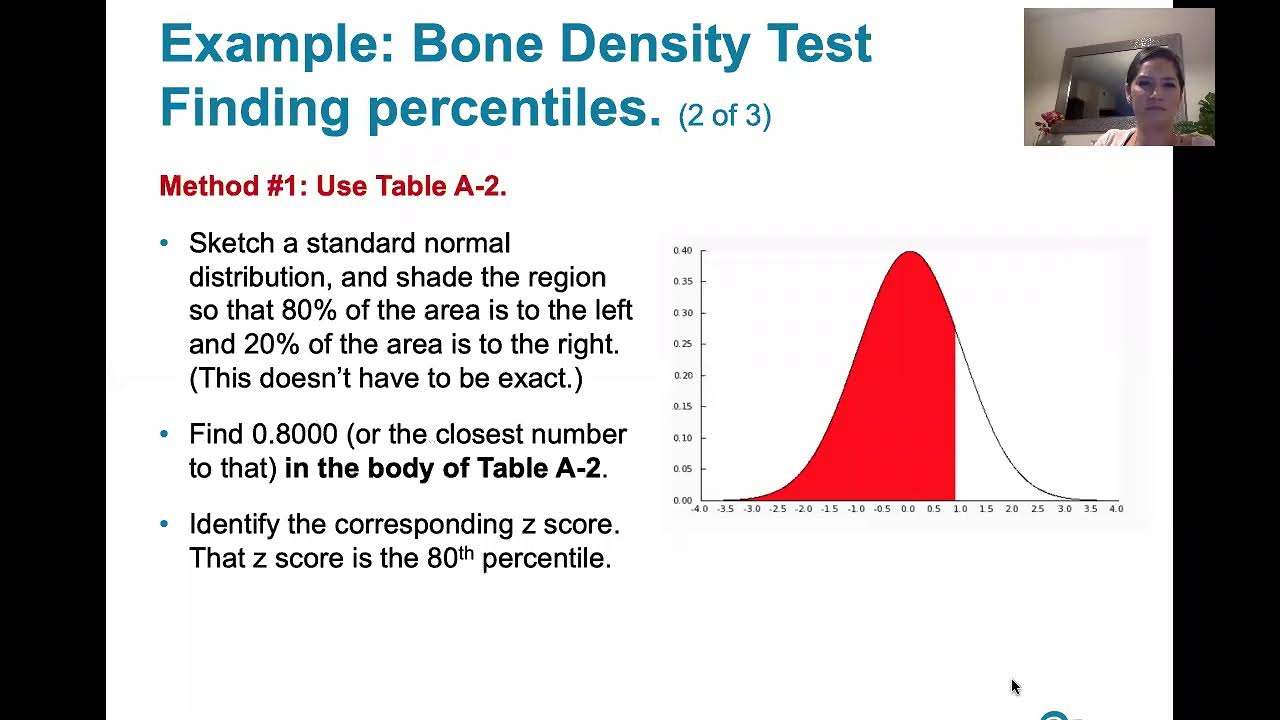
6.1.5 Standard Normal Distribution - z scores Corresponding to Areas. Percentiles. Critical Values.

Finding P-Value for a Z-Test Using the TI-84

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Z-TableStatisticsP-ValueDistributionProbabilityData AnalysisResearch ToolStatistical SignificanceNormal DistributionObservations