Unit I: Lec 5 | MIT Calculus Revisited: Single Variable Calculus
TLDRThis MIT OpenCourseWare lecture delves into the rigorous approach to limits, emphasizing the importance of mathematical definitions in problem-solving. The professor reviews the fundamental limit definition and illustrates how to apply it to various scenarios, including limits of constants, variables, and sums and products of functions. The lecture aims to demystify the concept of limits and demonstrate how theorems can be derived from basic definitions to align with intuitive understanding, solidifying the foundation for more complex mathematical analysis.
Takeaways
- 📚 The lecture is part of a series on limits, aiming to provide a more rigorous approach to understanding them through mathematical definitions.
- 🔍 The fundamental definition of a limit is reviewed, emphasizing the relationship between epsilon and delta, and the process of proving limits without allowing 'x' to equal 'a'.
- 📉 The importance of choosing the correct neighborhood around 'a' when dealing with functions that are not one-to-one is highlighted to avoid errors in limit calculations.
- 📝 The concept of proving theorems rigorously is introduced, starting with simple cases like the limit of a constant function and gradually moving to more complex scenarios.
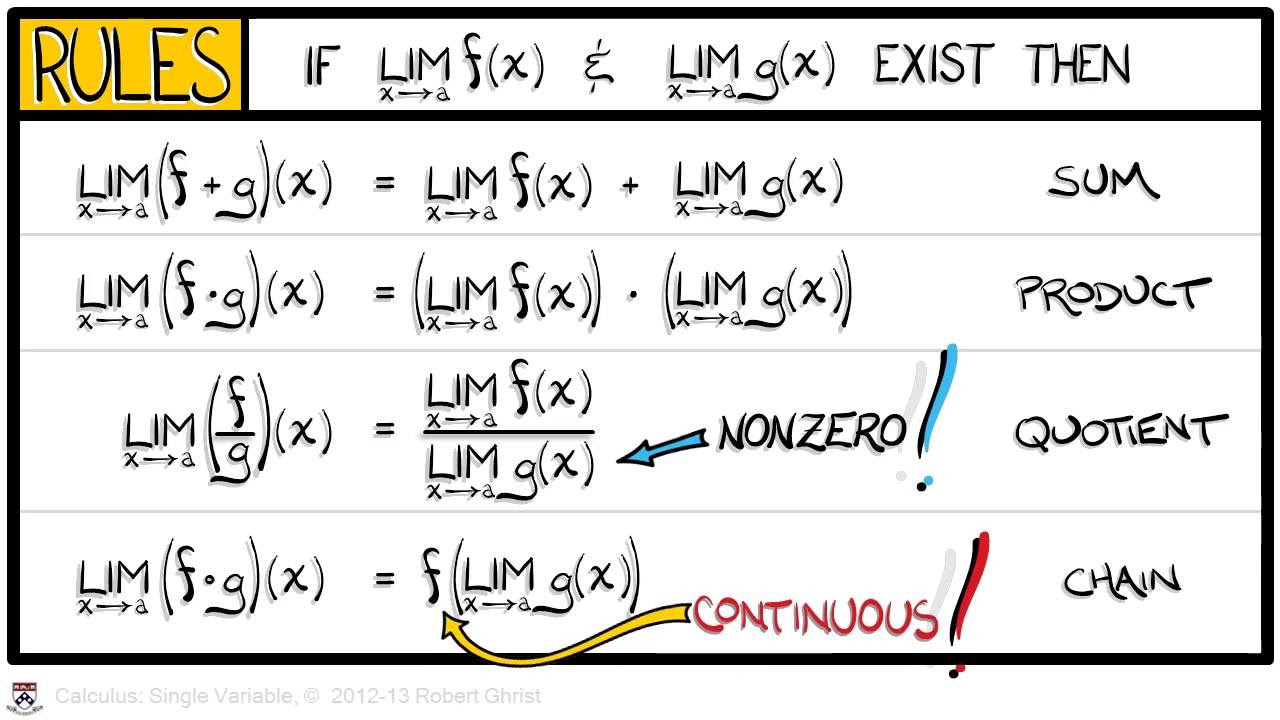
- 🔢 A theorem is proven that the limit of a sum of functions is equal to the sum of their individual limits, illustrating the process with a detailed, step-by-step mathematical approach.
- 📈 The graphical representation of limits is discussed, with the emphasis on not relying solely on diagrams and ensuring that proofs are independent of any particular visual representation.
- 🤔 The potential for incorrect reasoning in limit proofs is cautioned against, and the importance of rigorous mathematical proof is underscored.
- 📚 The process of reverse-engineering a proof by starting with the desired result and working backward to fit the definition is explained, demonstrating a common mathematical strategy.
- 🔄 The necessity of using different delta values for different parts of a proof is justified, showing that the same epsilon can require different deltas depending on the function's behavior.
- 📘 The script concludes with a discussion on the practical applications of limit theorems, such as finding the limit of a polynomial expression by applying previously proven theorems.
- 🌟 The overall goal of the lecture is to demonstrate how mathematical theorems can simplify the process of finding limits, allowing for easier application in various problems.
Q & A
What is the main objective of the lecture titled 'Limits: a More Rigorous Approach'?
-The main objective of the lecture is to help students gain experience with using limit expressions and absolute values, and to demonstrate how well-defined mathematical definitions can be used to solve certain types of problems related to limits.
What is the fundamental definition of a limit as described in the script?
-The limit of 'f(x)' as 'x' approaches 'a' equals 'l' means that for each epsilon greater than 0, there exists a delta greater than 0 such that whenever the absolute value of 'x - a' is less than delta, the absolute value of 'f(x) - l' will be less than epsilon.
Why is it important to not allow 'x' to equal 'a' when discussing limits?
-It is important because the limit definition is concerned with the behavior of 'f(x)' as 'x' gets arbitrarily close to 'a', but not necessarily at 'a' itself. This prevents issues such as division by zero or other undefined behaviors at the point 'a'.
How does the script illustrate the concept of delta in relation to a limit?
-The script uses a graphical approach, showing that delta is the minimum distance from point 'a' to the end points of the interval where 'f(x)' is within the epsilon neighborhood of 'l', emphasizing the local behavior near 'a'.
What is the significance of the theorem stating that the limit of a constant 'c' as 'x' approaches 'a' is 'c'?
-This theorem is significant because it establishes a basic property of limits for constant functions, showing that the limit of a constant value does not change regardless of the approach to any point 'a'.
How does the script prove that the limit of a constant function is the constant itself?
-The script proves it by showing that for any epsilon greater than 0, one can choose any delta greater than 0, and 'f(x)' which is the constant 'c', will always be within epsilon of 'l', which is also 'c', because 'c - c' is 0, automatically less than any positive epsilon.
What is the geometric interpretation of the limit of 'x' as 'x' approaches 'a' being equal to 'a'?
-The geometric interpretation is that as 'x' gets arbitrarily close to 'a', the value of 'x' itself gets arbitrarily close to 'a'. This is represented graphically by the straight line 'y = x', where the y-coordinate (value of 'x') is equal to the x-coordinate (approach to 'a').
What is the importance of proving that the limit of a sum is equal to the sum of the limits?
-This theorem is important because it provides a fundamental property of limits that allows for the simplification of limit calculations by finding the limits of individual functions and then summing those results, rather than finding the limit of the entire expression directly.
How does the script handle the proof of the limit of a sum being equal to the sum of the limits?
-The script outlines a rigorous proof by using the definition of limits and the properties of absolute values, showing that for any given epsilon greater than 0, one can find a suitable delta such that the sum of the functions is within epsilon of the sum of their limits.
What is the key takeaway from the lecture regarding the approach to understanding and proving limits?
-The key takeaway is the importance of using rigorous, well-defined mathematical definitions and theorems to understand and prove limits, rather than relying solely on intuition or graphical interpretations, which can sometimes be misleading.
Outlines
📚 Introduction to Rigorous Limits
The narrator introduces the video as part of MIT OpenCourseWare under a Creative Commons License, encouraging donations for free educational resources. The professor greets the audience and outlines the lecture's objective to explore limits with a rigorous approach. The fundamental definition of a limit is reviewed, emphasizing the relationship between epsilon and delta, and the importance of not allowing 'x' to equal 'a'. The professor uses geometric interpretations to clarify the concept and stresses the significance of mathematical definitions in problem-solving.
📐 Understanding Limit Definitions and Diagrams
The professor delves deeper into the definition of limits, discussing the geometric representation of limit concepts. He explains the process of finding delta for a given epsilon in the context of a function's graph. The importance of focusing on the neighborhood of point 'a' is highlighted, along with the caution against assuming that the curve's behavior elsewhere will mirror the neighborhood of 'a'. The professor also warns against relying too heavily on diagrams and emphasizes the need for a formal, analytical proof.
🔍 The Limit of a Constant Function
The lecture continues with a discussion on the limit of a constant function, demonstrating that the limit of 'c' as 'x' approaches 'a' is 'c'. The professor provides a proof using the basic definition of limits, showing that for any epsilon greater than 0, a suitable delta can be found to ensure that 'f(x)' is within epsilon of 'l'. The geometric interpretation of this concept is also provided, illustrating that the output of a constant function is uniform across its domain.
🤔 The Limit of a Function as x Approaches a
The professor introduces the theorem that the limit of 'x' as it approaches 'a' is 'a' itself. This theorem is self-evident, but the professor emphasizes the importance of rigorous proof over intuition. By comparing the definitions and using the properties of absolute values, it is shown that for any given epsilon, a delta can be chosen such that 'x' is within epsilon of 'a', without actually being equal to 'a'.
📘 Sum of Limits and Limit of Sums
The lecture progresses to a critical theorem stating that the limit of the sum of two functions is equal to the sum of their individual limits. The professor warns against assuming this property is self-evident and explains the importance of proving such properties. The proof involves defining new functions and using the properties of limits to show that for any given epsilon, appropriate delta values can be found to satisfy the theorem's conditions.
🔗 Combining Functions and Their Limits
The professor discusses the importance of ensuring that functions have a common domain when defining their sum or product. The domain of the new function 'h' is defined as the intersection of the domains of 'f' and 'g'. The lecture emphasizes the need to consider the domain when working with functions and their limits, especially when combining them.
📚 Proof of the Sum of Limits Theorem
The professor provides a detailed proof of the sum of limits theorem. By defining new epsilon values as half of the original epsilon, the proof shows that for these values, delta can be chosen such that the sum of the functions 'f(x)' and 'g(x)' is within epsilon of the sum of their limits 'l1' and 'l2'. The proof is made rigorous by carefully selecting deltas and using the properties of absolute values.
📈 The Limit of a Product of Functions
The lecture explores the concept of proving the limit of a product of two functions. The professor outlines an alternative method involving the addition and subtraction of terms to create expressions that can be controlled using the limit definitions. The proof involves algebraic manipulation and the application of the limit properties to show that the product of the limits can be made arbitrarily close to the desired value.
📝 The Importance of Epsilon-Delta Proofs
The professor emphasizes the importance of epsilon-delta proofs in establishing the foundation for understanding limits. While these proofs may not be needed for simple applications of limit theorems, they are essential for proving theorems and solving more complex problems that may arise in real-life situations.
📑 Conclusion and Acknowledgment
The professor concludes the lecture by summarizing the importance of rigorous proofs in mathematics and the utility of epsilon-delta definitions. The video's funding is acknowledged, and viewers are encouraged to support MIT OpenCourseWare to ensure continued access to educational resources.
Mindmap
Keywords
💡Limits
💡Epsilon-Delta Definition
💡Rigorous Approach
💡Theorem
💡Intuitive Terms
💡Function
💡Domain
💡Intersection
💡Absolute Value
💡Summation of Limits
💡Product of Limits
Highlights
Introduction to a more rigorous approach to understanding limits in mathematical definitions and problem-solving.
Fundamental definition of a limit, emphasizing the relationship between epsilon and delta for any function 'f(x)' as 'x' approaches a point 'a'.
The importance of not allowing 'x' to equal 'a' in the limit definition to avoid undefined expressions.
Geometric interpretation of the limit definition using a diagram to illustrate the concept near a point 'a'.
Explanation of how the width of intervals in a diagram does not necessarily project equally onto the 'y'-axis, emphasizing the need for careful neighborhood selection around 'a'.
The concept that any valid delta can be replaced by a smaller one, reinforcing the idea that limits are not sensitive to small changes in 'x'.
The process of proving mathematical theorems rigorously using the definition of limits, starting with simple theorems and progressing to more complex ones.
Proof that the limit of a constant 'c' as 'x' approaches 'a' is 'c', illustrating the use of epsilon and delta in a straightforward case.
The geometric interpretation of the limit of a constant, showing that 'f(x) = c' results in a horizontal line at 'c' on the graph.
The caution against relying on diagrams for proofs, emphasizing the need for formal, analytic proofs that are independent of graphical representations.
The proof that the limit of 'x' as 'x' approaches 'a' is 'a', demonstrating a self-evident theorem using epsilon and delta.
The theorem stating that the limit of a sum is equal to the sum of the limits, with a detailed explanation of its proof.
The importance of ensuring that functions involved in a sum have a common domain before taking the limit of their sum.
The method of using separate delta values for different parts of a limit proof, and how to combine them to satisfy the overall condition.
The intuitive approach to proving the limit of a product equals the product of the limits, using algebraic manipulation and the properties of absolute values.
The application of limit theorems to practical problems, such as finding the limit of 'x squared plus 7x' as 'x' approaches 3, without direct substitution.
The role of epsilon and delta in the backbone of limit theory, and how theorems derived from them can simplify problem-solving.
The conclusion emphasizing the importance of understanding and applying rigorous mathematical definitions and theorems in problem-solving.
Transcripts
Browse More Related Video

Unit II: Lec 1 | MIT Calculus Revisited: Single Variable Calculus

Unit I: Lec 4 | MIT Calculus Revisited: Single Variable Calculus

Calculus Math 133 - Lecture 2.2

Lecture 13: Achilles, Tortoises, Limits and Continuity

AP Calculus AB - 1.5 Determining Limits Using Algebraic Properties of Limits
Calculus Chapter 1 Lecture 7 Limits
5.0 / 5 (0 votes)
Thanks for rating: